环肋导管桨推进性能分析

卓恒，刘鹏，尚志强，2，王思琦，辛龙庆，张昭鹏

（1.中国海洋大学 山东省海洋工程重点实验室，山东 青岛 266100；2.河口黄河河务局，山东 东营 257231）

在中国明确“2030 年前实现碳达峰，2060 年前实现碳中和”的目标并向全球郑重承诺后，减碳已成为当前全社会所面临的共同任务［1］。海路运输相对于陆路运输有着运量大、距离长、网络密集、发展成熟和费用低廉的优势，因此，当今世界国际贸易量的95%以上都是通过船舶运输来完成的；同时船运相对于其他运输方式具有最低温室气体排放率，统计表明：船运业的二氧化碳排放只占人类活动总排放量的3%左右，这表明船运是最绿色的运输方式［2］。

随着经济全球化的加速发展，海上运输需求日益增长，但船舶在运营过程中会产生大量氮氧化物NOX、硫氧化物SOy等有害物质，严重威胁着全球环境和人类安全健康，国际海事组织（international maritime organization,IMO）已相继出台了一系列法规要求减少船舶带来的环境污染问题。因此，对船舶进行节能减排技术研究，提高能源的利用率，降低船舶营运成本，减少有害物质对环境的污染，有十分重要的现实意义［3］。

作为船舶主要的推进器，螺旋桨因具有构造简单、使用方便、推进效率较高等优点在船舶上得到广泛应用。国际海事组织提出的船舶设计能效指标（energy efficiency design index,EEDI）已于2015 年开始强制执行［4-5］。螺旋桨要达到良好的船舶节能效果，必须进一步提高推进效率，使船舶在保持航速不变的条件下能够降低主机的功率。

导管桨因其相较于普通螺旋桨的巨大优势，国内外很多专家和学者对其进行了大量的研究：螺旋桨毂帽鳍（propeller boss cap fins，PBCF）在20 世纪由日本三井造船大内一之等提出，与其他节能装置相比，它具有结构简单、故障少、安装便捷、成本低、节能效果显著等优点［6］。目前，国内外对于毂帽鳍的性能预报以及参数设计优化基本上是针对模型尺度下的敞水工况进行的［7-11］。

尚志强等［12］利用计算流体力学分析和实验验证的方法，对依据仿生学原理在导管后半段增加锯齿状突起进行了研究，研究发现仿生尾缘导管桨更适用于高进速系数下，能够提高效率，减少螺旋桨运行时的噪声。高洪涛等［13］利用计算流体力学(compu‐tational fluid dynamics,CFD)方法在不同雷诺数下研究了仿生前缘凸起舵的流场，揭示带有前缘凸起的舵的流动机理。Majdfar 等［14］运用CFD 软件研究了螺旋桨在导管内的位置和导管角度对螺旋桨水动力性能的影响。Taketani 等［15］提出一种具有高推进效率的导管螺旋桨推进器的设计方法；Koronoeicz等［16］系统设计了一种加速导管螺旋桨。

Szafran 等［17］利用计算流体力学和实验方法对一种具有新型气动外形的导管进行了研究，结果表明新型导管桨在中高进速时有更好的水动力性能和推进效率。Shin等［18］采用数值和实验设计方法对包括非常规半圆形导管和常规圆形导管在内的预涡流导管进行了研究，发现预涡流导管能够使超大型油轮（very large crude carrier，VLCC）的螺旋桨推进系统获得较大的增益。Bhattacharyya等［19］基于湍流模型利用CFD 方法分析了在转捩状态下导管桨的水动力性能。Villa 等［20］采用实验和计算流体力学的方法分析加速和减速导管桨的水动力性能和流场，基于现代高保真粘性计算流体动力学代码准确预测这两种类型导管桨的性能和流场。

对于远洋货轮来说，更需要的是一种能够在高进速以及重载荷的工况下，也能够有更高的推进性能和推进效率的螺旋桨推进器。环肋导管桨是一种导管螺旋桨附加节能装置，环肋与导管一体铸造成型，降低额外机构失效的可能性，减小船尾的水流分离与粘压阻力。螺旋桨旋转时带动周围的水分子运动，其流线呈螺旋状，水分子的运动方向可以分解为轴向、周向和径向运动。环肋能够回收部分能量。同时，环肋的存在阻碍水分子的运动，根据力的相互作用，导管桨也会获得额外的推力。

本文以带有环肋结构的33+Kd5-100 导管螺旋桨为研究对象，以CFD 方法分析其水动力性能，并与无此环肋结构的33+Kd5-100 型号导管螺旋桨做对比，验证其节能效果，为降低船舶的能耗需求提供技术支持。

1 几何模型与数值方法

以33+Kd5-100减速导管螺旋桨为模型，使用移动参考坐标系(moving reference frame,MRF)模型计算其水动力性能，着重分析了不同网格数量对螺旋桨的数值模拟结果的影响，并与试验值结果进行比较，对CFD计算方法的可靠性进行验证。

1.1 物理模型与网格划分

Kd5-100 螺旋桨的直径为0.25 m，叶数为5，P/D为1，纵倾角和侧斜角均为0°，三维物理模型如图1所示。

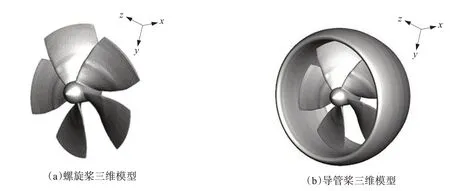
图1 螺旋桨和导管桨三维模型Fig.1 3-D model of propeller and ducted propeller

本文在对导管桨进行网格划分时，采用结构化方法，可大大节约网格数量，缩短计算时间。采用多重移动参考模型进行数值模拟计算［21］，并将计算域划分为旋转动域和静止域。根据文献［12,22-23］计算域直径为3D，长度为7D（D为螺旋桨模型直径），其中设置桨盘面到入口的长度为3D，桨盘面到出口的长度为4D，能够满足流场的充分发展，所以本文的螺旋桨计算域依此进行划分。

静止域整体采用六面体结构网格划分，为保证网格质量，在划分网格时，将包含导管的区域单独划分为一个小域。因导管外表面为不规则圆柱体，故而在此小域中将靠近导管首尾末端区域再次分割。整个静止域被划分为60个结构块。

与普通螺旋桨稍有区别的是：在设置导管桨的旋转域时，由于导管并不随螺旋桨旋转，因此，螺旋桨的旋转域中只包含螺旋桨，而导管模型建立在大域中。这样，考虑到导管与螺旋桨叶梢的间距很小，需要对旋转域中螺旋桨叶梢处的网格进行加密处理才能够保证计算的精确度。为了在计算时减小误差，动域是以导管内表面为轮廓。因为螺旋桨的结构非常复杂，包含螺旋桨的旋转动域采用四面体非结构网格划分。

最终，整个计算域一共被划分了61 块结构体和200万网格，单就螺旋桨所在的区域划分了126万网格，这是因为桨叶叶稍紧靠区域边界且桨叶是不规则的扭曲叶面，需要在桨叶叶稍区域进行局部加密来保证网格质量。网格分块划分如图2所示。

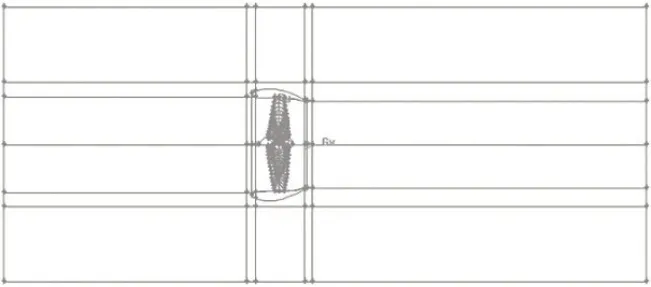
图2 网格分块划分示意Fig.2 Schematic diagram of mesh partition

计算域边界条件入口和出口处分别采用速度入口和压力出口，计算域圆柱体外边界、桨叶、桨毂及导管边界面均采用无滑移壁面条件。

包含螺旋桨的域为动域，其余部分为静域。如图3所示，动域的网格为非结构化网格，对桨叶叶梢部分进行网格加密，导管前后缘采用源面的方式划分体网格。由于导管内壁紧靠螺旋桨的叶稍，该部分划分为圆环结构，该结构采用结构化网格并进行加密，进流段和出流段以及导管桨区域的剩余部分均采用结构化网格划分，动域和静域的交界面设置为交界面。在保证计算精度的同时尽可能减少网格数量。

图3 计算域网格梢隙网格Fig.3 Computational domain grid and tip gap grid

包含螺旋桨的旋转动域采用移动参考坐标系方法，以x轴为旋转轴，速度600 r/min 旋转运动，通过改变来流速度的方式进行进速系数的转换。使用Fluent软件基于有限体积法求解雷诺平均 N-S 方程（简称 RANS 方程），湍流模型采用RNGk-ε，采用三维单精度基于压力隐式求解器，耦合方式采用压力耦合方程组的半隐式方法（semi-implicit-method for pressure linked equations,SIMPLE），离散格式采用二阶迎风格式，对导管桨的定常水动力性能进行计算，计算结果收敛后停止迭代［12］。图4（a）为桨叶表面网格，图4（b）为x=0处剖面网格。

图4 桨叶表面网格和剖面网格Fig.4 Blade surface grid and section grid

1.2 控制方程

假定流体是不可压的，则导管螺旋桨在水下运动过程中周围流场的连续方程和动量方程分别为：

式中：ui、uj为速度分量时均值（i，j=1，2，3）；p为压力时均值；ρ为流体密度；u为流体黏性系数；gi为重力加速度分量为雷诺应力项。

到目前为止，湍流的内在机理还在不断研究中，至今解决湍流问题主要还是采用湍流模型［24-26］。湍流模型选取RNGk-ε模型，它是标准k-ε模型的改进公式，由于考虑了湍流旋涡，因此能更好地处理螺旋桨的旋转问题［27］，其方程为：

式中：Kp为螺旋桨的推力，N；Kd为导管的推力，N；Q为螺旋桨的扭矩，Ν·m。

2 数值方法验证

2.1 模拟网格收敛性分析

为了讨论分析网格数对导管螺旋桨水动力性能的影响，依次划分网格数量为58 万、200 万、360 万，湍流模型采用RNGk-ε，入口长度为3D，其余参数设置均相同，计算结果见表1，其中误差的百分比为计算值与实验值的差值比上实验值。

表1 不同网格数的计算值与实验值的误差Table 1 Error between calculated and experimental values of different grid numbers %

如表1 所示，计算值与实验值的误差在不同网格数量下相差很小，网格数量的变化对推力系数、扭矩系数以及效率的影响很小。因此，在接下来划分导管桨的网格时，在保证网格质量的前提下，尽量减少网格数量，兼顾求解效率与精度。

2.2 数值验证与误差分析

为了验证第1 节所提到的计算模型的准确性，本文使用该计算方法计算了33+Kd5-100 型导管桨的推进性能，并与试验数据进行对比。图8 给出了不同进速下螺旋桨的推进性能。

图5 描述的是33+Kd5-100 减速导管桨的计算值和文献［28］实验值的曲线图。随着进速系数的增大，计算值和实验值的曲线变化趋势相同。同时，推力系数、扭矩系数和效率的计算值与实验值之间的误差一直在增大。

图5 33+Kd5-100型导管桨推进系数的计算值与试验值比较Fig.5 Comparison between calculated and experimental values of propulsive coefficient of 33+Kd5-100 duct‐ed propeller

存在误差的原因主要由2 部分构成：1）数值模型和实验模型存在出入，数值计算过程中离散方程的截断误差以及舍入误差也是不容忽略的，同时实验设备以及实验条件的设置也能够引起误差；2)利用Fluent软件模拟螺旋桨的敞水性能是在理想状态下进行的，这在现实中是不可能达到的。

总的来说，利用以上提出的数值模拟方法和多分区混合型网格划分方法模拟导管桨的推进性能是可行的，满足模拟精度要求。

3 环肋导管桨推进性能及影响因素分析

图6、7 给出了Kd5-100 螺旋桨和33 导管改进后的环肋导管桨模型。借用三维建模软件对33 导管内部增加环肋结构，以导管后半段内侧为附着面，环肋剖面为等腰三角形，环肋数量为c，环肋横剖面高度为h，环肋剖面角度为a。

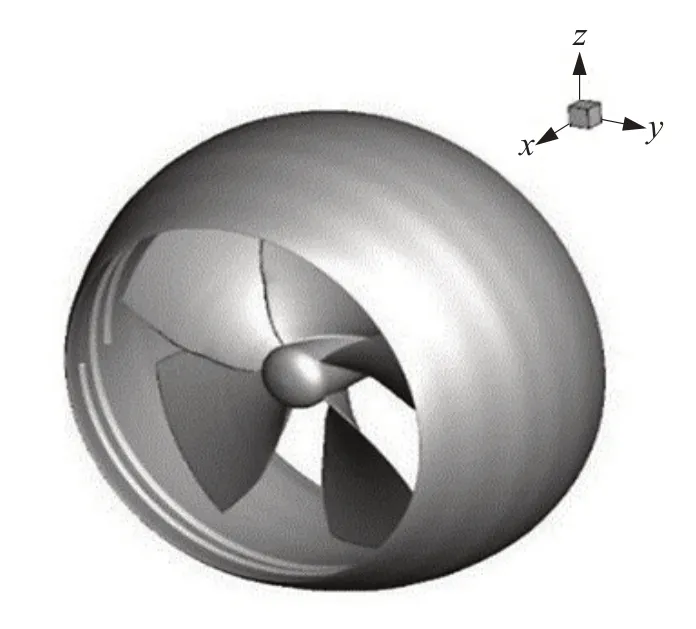
图6 环肋导管桨Fig.6 Ring rib ducted propeller

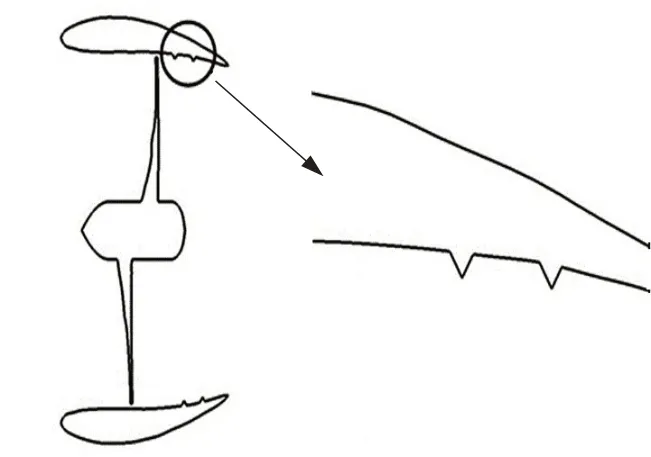
图7 环肋导管桨横截面Fig.7 Cross section of ring rib ducted propeller

对于图6 中的环肋导管桨模型，由于在导管内侧增加环肋结构，以及导管内壁和螺旋桨叶稍间距相对较小，因此采用多分区混合型网格划分方法对求解域进行细致的划分。基于上文采用的多分区混合型网格划分方法，选取a=60°，h=2 mm，c=2 圈，环肋旋向为逆时针方向（由叶背指向叶面）作为环肋导管桨的初始参数，采用控制变量的方法来研究结构参数对环肋导管桨推进性能的影响。

3.1 环肋数量

本节将讨论环形肋数量对导管桨推进性能的影响，首先定义环形肋结构围绕导管内壁的回转圈数为环肋的数量。如图8 所示，改变环肋数量c为1圈、2 圈和3 圈，固定a=60°，h=2 mm，环肋旋向为逆时针，研究环肋圈数与导管桨的推进性能之间的关系，如图9所示。图9和表2给出了不同环肋圈数导管桨与常规导管桨的推进性能对比。

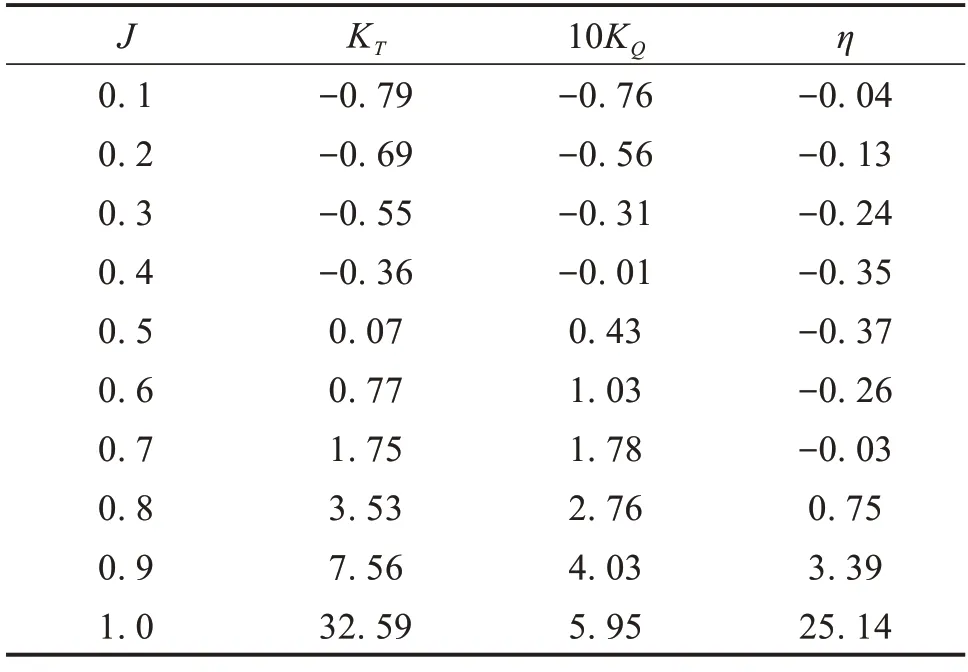
表2 环肋导管桨相对常规导管桨推进系数提升百分比（a=60°，h=2 mm，c=1圈）Table 2 Percentage increase of propulsion coefficient of ring rib guide propeller relative to conventional guide propeller (a=60°,h=2 mm,c=1 circle) %

图8 环肋数量Fig.8 Number of ring ribs

图9 不同环肋数量推进性能曲线Fig.9 Propulsion coefficient curves of different number of ring ribs

由图9（a）中可以看到环肋导管桨的推力系数较常规导管桨有很大幅度的提升，从表2 推力系数这一列中可知随着进速系数的增加，推力系数的提升幅度也在增加，且J=0.8 对应的推力系数提升幅度超过J=0.7 的一倍以上。当J=1.0、c=1 时，推力系数提升幅度的最大值为32.59%。圈数的改变对推力系数的影响很大，整体上是随着圈数的增加，推力系数在减小。

由图9（b）中可以看到环肋导管桨的扭矩系数较常规导管桨有一定幅度的提升，并且从表2 扭矩系数这一列中可知随着进速系数的增加，扭矩系数的提升幅度也在增加。当J=1.0、c=1 时，扭矩系数提升幅度的最大值为5.95%。圈数的改变对扭矩系数的影响很小，随着圈数的增加，扭矩系数也在减小。

由图9（c）中可以看到当J＜0.7 时，环肋导管桨的效率低于常规导管桨；当J≥0.7 时，效率高于常规导管桨。从表2效率这一列中可知随着进速系数的增加，当J＜0.7，环肋导管桨与常规导管桨效率之间的差距在缩小；当J≥0.7 时，效率的提升幅度在增加。当J=1.0、c=1 时，效率提升幅度的最大值为25.14%，从表2 推力系数和扭矩系数这2 列中可知在J=1.0 时，推力系数的提升幅度远高于扭矩系数的提升幅度，导致了在此进速系数时的效率的大幅度提升。圈数的改变对效率的影响很大。

由此得出结论：环肋导管桨的推力系数和扭矩系数在高进速系数时均大于常规导管桨，当c=1，推力、扭矩系数提升幅度最明显，最大值分别为32.59%和5.95%。当J＜0.7时，环肋导管桨的效率低于常规导管桨；当J≥0.7 时，环肋导管桨的效率高于常规导管桨，效率提升幅度的最大值为25.14%。环肋圈数的变化对其推进性能的影响较大。

3.2 环肋横截面积

本节将讨论环形肋的横截面积对导管桨性能的影响。如图7 所示，环形肋结构的横剖面为等腰三角形，此等腰三角形的高为h。本节为讨论单一参数的影响，将通过改变环肋高度、保持顶角角度不变而获得不同的横截面积。如图10所示，环肋剖面为等腰三角形，固定a=60°，c=2 圈，改变环肋横剖面高度h=1、2、3、4mm 来改变环肋横截面积，环肋旋向为逆时针。研究横截面积与环肋导管桨的推进性之间的关系，如图11所示。

图10 环肋横截面积Fig.10 Cross sectional area of ring rib

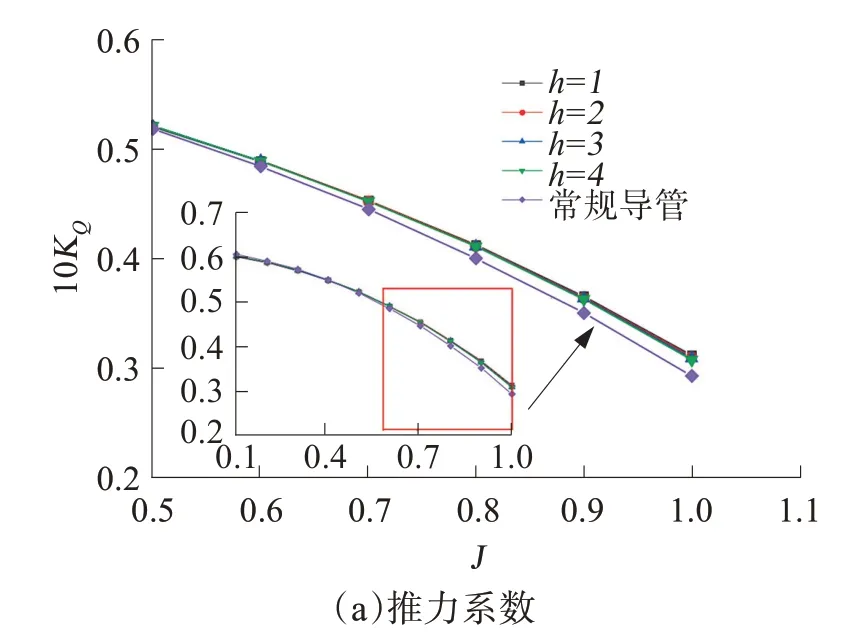
图11 不同环肋横截面积推进性能曲线Fig.11 Propulsion performance curves of different ring rib cross-sectional areas

图11和表3、4给出了不同环肋横截面积导管桨与普通导管桨的推进性能对比。由图11 可以看出环肋导管桨的推进性能较普通导管桨有很大的提升，并且从表3、4可知随着进速系数的增加，推力系数、扭矩系数和推进效率的提升幅度也在增加，且最大值在J=0.1时。

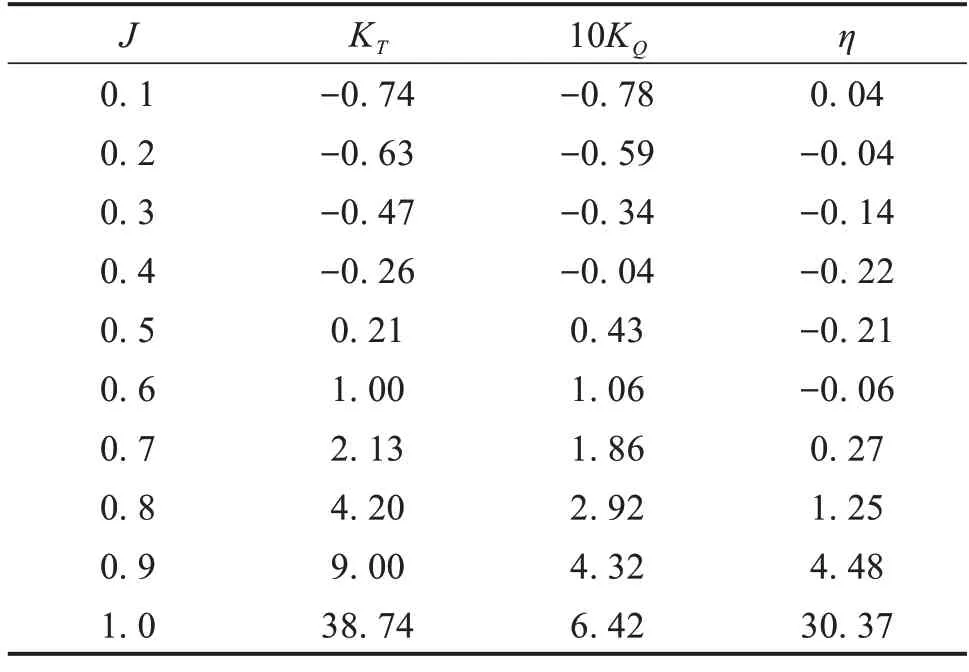
表3 环肋导管桨相对常规导管桨推进系数提升百分比（a=60°，h=1mm，c=2圈）Table 3 Percentage increase of propulsion coefficient of ring rib guide propeller relative to conventional guide propeller (a=60°,h=1mm,c=2 circle) %

由图11 中可以看到，环肋导管桨分别在J=0.7、0.4、0.9 时，其推力系数、扭矩系数和推进效率均大于常规导管桨。环肋剖面高度h=1、2、3、4 mm 时，推力系数的提升幅度最大值为38.74%、29.80%、20.74%、12.01%；扭矩系数提升幅度最大值为6.42%、5.98%、5.49%、5.21%；推进效率提升幅度最大值为30.37%、22.47%、14.46%和6.47%。由此可以看出，环肋横截面积的增加，推力系数和推进效率的最大提升在大幅度减小，而扭矩系数的提升幅度减小很少，这也正是推进效率提升减小的原因，并且环肋横截面积对导管桨的推进效率影响很大，差值达到了14%。

整体上随着环肋横截面积的增加，推力系数在减小，环肋横截面积的变化对推力系数影响较大。横截面积的改变对扭矩系数的影响很小，随着横截面积的增加，扭矩系数在减小。由图14 及表3 和表4 中可以看到剖面高度的改变对推进效率的影响很大，随着剖面高度的增加，推进效率在减小。不过在a=60°、h=1 mm、c=2圈时，此环肋导管桨的推进效率提升很明显，当J＜0.7 时，环肋导管桨的效率均低于常规导管桨；当J≥0.7 时，环肋导管桨的效率高于常规导管桨。随着进速系数的增加，各横截面积对应效率之间的差值也在增大。

表4 环肋导管桨相对常规导管桨推进系数提升百分比（a=60°,h=4mm,c=2圈）Table 4 Percentage increase of propulsion coefficient of ring rib guide propeller relative to conventional guide propeller (a=60°, h=4mm,c=2 circle) %

由此得出结论：随着进速系数的增加，推力系数和扭矩系数的提升幅度在增加；随着横截面积的增加，推力系数和扭矩系数的提升幅度在减小。在a=60°、h=1mm、c=2 圈时，此环肋导管桨的推进效率提升很明显。当J＜0.7 时，环肋导管桨的效率低于常规导管桨；当J≥0.7 时，环肋导管桨的效率高于常规导管桨，且随着进速系数的增加，各横截面积对应效率之间的差值在增大。环肋横截面积对导管桨的推进效率影响很大。

3.3 环肋剖面角度

如图12 所示，改变环肋横剖面等腰三角形的顶角的角度a分别为60°、90°、120°，固定h=2mm，c=2圈，环肋旋向为逆时针，研究剖面角度与环肋导管桨水动力性能之间的关系，如图12 所示。图12 和表4给出了不同环肋剖面角度导管桨与常规导管桨推进性能对比。

图12 环肋剖面角度Fig.12 Ring rib section angle

由图13 中可以看到改变剖面角度后，环肋导管桨的推力系数、扭矩系数和推进效率较常规导管桨同图9、11 一样均有较大幅度的提升；从表5 中可以看到随着进速系数的增加，环肋导管桨的推进系数的提升幅度也在增加，当J=1.0 时，提升幅度最大。由图13 中可以看出，随着进速系数的增加，推力系数和扭矩系数在减小，推进效率先增大后减小，且环肋导管桨的推力系数（J≥0.5）、扭矩系数（J≥0.4）和推进效率（J≥0.7）分别均大于常规导管桨。3 种不同环肋剖面角度a分别为60°、90°、120°（下同），其推力系数较常规导管桨的最大提升幅度为29.80%、32.43%、36.57%，随着剖面角度的增加，其推力系数的最大提升幅度也在增加，其差值达到7%，环肋剖面角度的改变对推力系数的影响很大。3 种不同环肋剖面角度的扭矩系数最大提升幅度为5.98%、6.06%、6.41%，随着剖面角度的增加，扭矩系数的提升幅度也在增加，但剖面角度的变化对扭矩系数的影响很小。3 种不同环肋剖面角度的推进效率最大提升幅度为22.47%、24.87%、28.35%，随着剖面角度的增加，推进效率提升幅度也在增加，剖面角度的变化对环肋导管桨推进效率的影响较大，这是因为剖面角度的改变对推力系数的提升远大于对扭矩系数的提升。

表5 环肋导管桨相对常规导管桨推进系数提升百分比（a=120°、h=2 mm、c=2圈）Table 5 Percentage increase of propulsion coefficient of ring rib guide propeller relative to conventional guide propeller (a=120 °, h=2 mm,c=2 circle) %

图13 不同剖面角度推进性能曲线Fig.13 Propulsion performance curves at different section angles

由此得出结论：随着进速系数的增加，推力系数和扭矩系数的提升幅度在增加。当J＜0.7 时，环肋导管桨的效率低于常规导管桨；当J≥0.7 时，环肋导管桨的效率高于常规导管桨。剖面角度的变化对推进性能影响较大。

3.4 环肋旋向

改变环肋的旋向，可能会影响螺旋桨尾流经过环肋时的旋转方向，这会对环肋导管桨的推进性能产生影响。如图14所示，改变环肋旋向分别为s、n，（s和n分别代表从叶背指向叶面时，环肋旋转方向分别为顺时针和逆时针）固定a=60°，c=2圈，h=2 mm，探究环肋旋向对导管桨推力系数、扭矩系数和效率的影响，如图15所示。

图14 环肋旋向Fig.14 Ring rib rotation direction

图15 不同环肋旋向的推进系数曲线Fig.15 Propulsion coefficient curves of different ring rib ro‐tation directions

从图15中可以看到曲线的变化趋势与图9、11、13 趋势一致，与常规导管桨相比，无论环肋的旋向是逆时针还是顺时针，环肋导管桨的推进性能和推进效率都有很大幅度的提升，但环肋旋向的变化对推力系数、扭矩系数以及效率影响非常小。这是因为虽然改变环肋的旋向会影响到螺旋桨尾流经过环肋时的旋转方向，但是环肋依然起到了整流的作用，回收了部分能量，为螺旋桨提供了额外的推力。

由此得出结论：环肋方向的变化对于环肋导管桨的推进性能的影响很小，甚至可以忽略环肋方向的变化造成的影响。

4 流场分析

4.1 桨叶压力分布对比

图16、17 是J=1.0、来流速度2.5 m/s、螺旋桨转速600 r/min 时导管改进前后的桨叶压力图（a=60°，c=2 圈，h=1 mm）。对比改进前后的桨叶压力分布图，得到推力增加的机理。

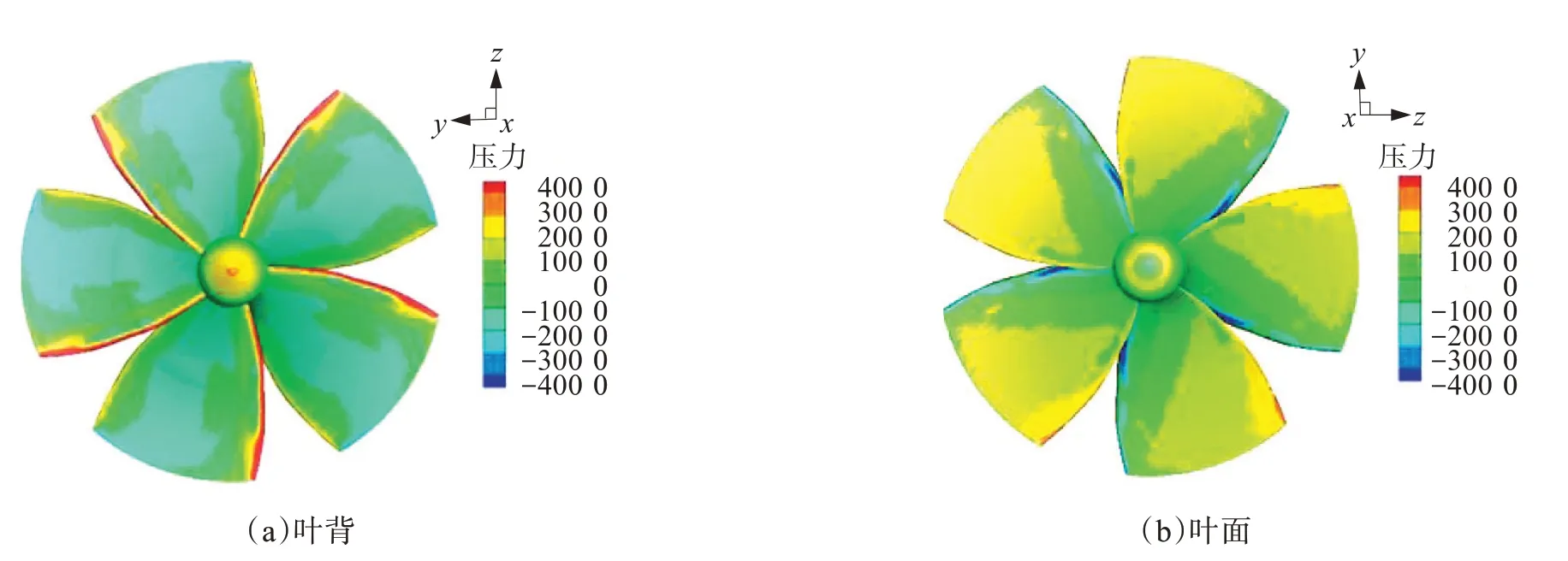
图16 常规导管桨桨叶压力分布Fig.16 Pressure distribution diagram of conventional ducted propeller blade

图17 环肋导管桨桨叶压力分布Fig.17 Pressure distribution of annular rib guide propeller blade

如图16、17 中的（a）图可以看到，增加环肋前后的叶背压力分布变化不明显。同时由图16、17 中的（b）图可以看到，增加环肋后的桨叶叶面导边的低压带减小，同时随边区域的高压区扩大，叶面压力增大，环肋导管桨推力的增大来源于叶面、叶背压力差的增大。但总的来说，螺旋桨叶片的压力变化并不是很大，这也解释了图9、11、13、15 当中推力系数曲线，在低进速时环肋导管桨与常规导管桨的区别并不是很大，而在高进速时环肋导管桨有很大的提升。这是因为在低进速时，螺旋桨的推力很大，环肋起到的作用并不明显，而在高进速时，螺旋桨的推力减小，此时环肋的作用就凸显出来。

4.2 导管压力分布对比

图18 是J=0.2、来流速度0.5 m/s、螺旋桨转速600 r/min时导管改进前后的压力分布图，图19是J=1.0、来流速度2.5 m/s、螺旋桨转速600 r/min 时导管改进前后的压力分布图（a=60°，c=2圈，h=1 mm）。

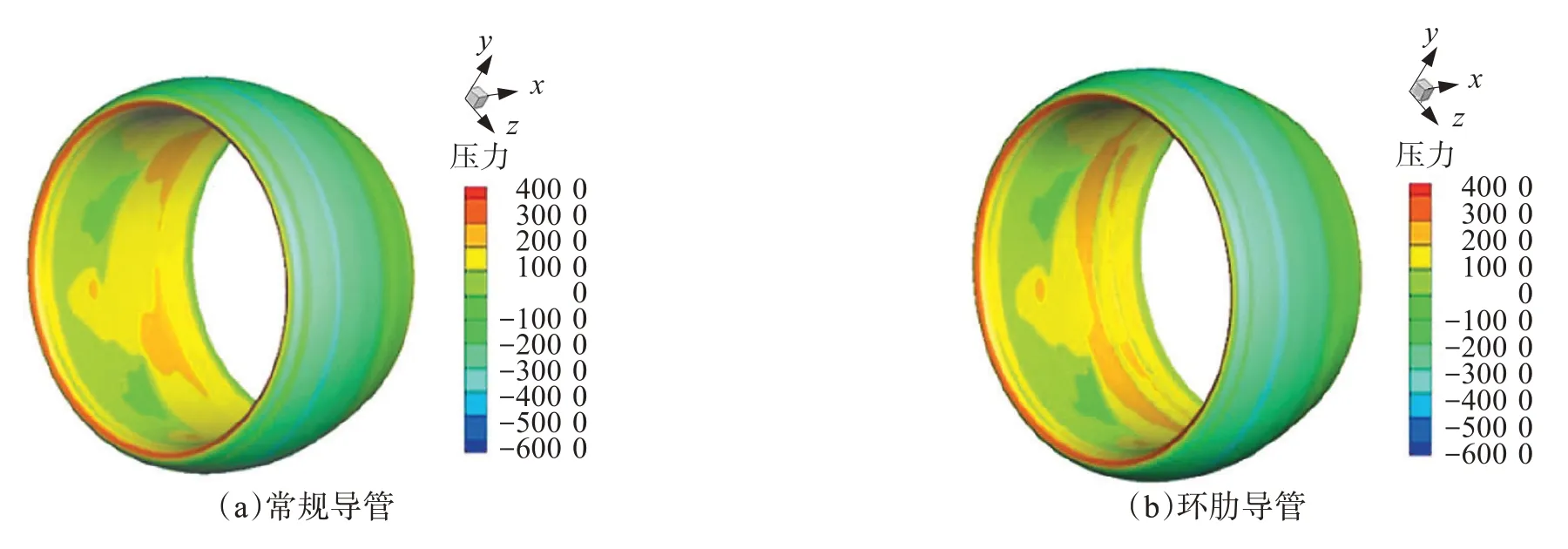
图19 J=1.0改进前后导管压力分布Fig.19 Pressure distribution diagram of conduit before and after improvement at J =1.0

由图18 可以看到，增加环肋前后的导管外壁面压力分布比较均匀，导管内壁面压力分布变化明显，此时导管产生的推力主要来自内壁面的压力变化。增加环肋前后的导管内壁面压力变化并不明显，甚至由于环肋的存在，使得导管内壁的高压区面积减小，说明当J=0.2 时，环肋导管提供的推力小于传统导管提供的推力，但是由于紧邻叶稍处最低压力区消失，减少了螺旋桨运行时的噪声。

由图19 可以看到，增加环肋前后的导管外壁面压力变化不明显，环肋导管内壁面的前半部分压力无明显变化，叶稍后出现高压区，且最大压力区域出现在环肋上。当J=1.0 时，导管提供的是阻力，阻碍船舶前进，环肋导管前后部分的压力差增加，环肋导管提供的阻力增加，但是环肋导管桨整体提供的推力大于传统导管桨，说明当J=1.0 时，环肋导管桨系统中的螺旋桨提供的推力占主要部分。

4.3 轴向速度分布对比

图20 是J=1.0、来流速度2.5 m/s、螺旋桨转速600 r/min 时常规导管桨和环肋导管桨（a=60°，c=2圈，h=1 mm）的轴向速度分布图。

图20 J=1.0改进前后导管轴向速度分布Fig.20 Axial velocity distribution of conduit before and after improvement at J=1.0

由图20 可以看到，导管增加环肋结构对轴向速度有一定的影响，环肋导管桨叶面后端的轴向速度由叶面一直持续到远处。环肋导管桨外部高速区面积增加，且环肋导管桨叶前的轴向速度较常规导管桨无变化，桨叶后变化比较明显。环肋导管桨在导管内部的高轴向速度区域的面积增加，低速区面积明显减小。尤其是导管后半段，低速区面积明显减小，在环肋周围的低速区域面积增大，并且在尾流后方远处，出现了高速区域。环肋导管桨获得的反向动量增加，增加导管桨的推力，导管改进后回收部分旋转能量，这也正是效率提升的原因。

5 结论

1)增加环肋结构后，环肋导管桨的推力系数、扭矩系数相较常规导管桨在高进速系数时有很大提升，提升幅度的最大值分别为38.74%和7.75%。随着进速系数增加，效率提升幅度增加，最大值为30.37%。环肋圈数、剖面角度和横截面积的变化都对推进性能有较大的影响，环肋旋向的变化对推进性能的影响很小。

2)导管增加环肋结构后，桨叶叶面导边低压得到改善并且叶背和叶面的压差增大，减少噪音的同时增加了螺旋桨推力。导管内壁高压集中在环肋结构之上，提高了导管的推力。轴向速度增加，螺旋桨获得的反向动量增加，说明导管改进后回收部分旋转能量，提升推进性能的同时也提高了效率。

3)结果表明，在圈数较少（如1 圈），横截面积较小，大角度时，环肋导管桨的推进性能和推进效率有大幅度提升。此环肋结构在高进速，重载荷船舶推进时有明显优势，在低进速时的推进性能及推进效率不如常规导管桨。因此，在制造高进速、重载荷船舶时，为符合高推进性能和高推进效率的绿色船舶发展趋势，可以选择适当的环肋结构参数，以满足设计需求。