三体船操纵性自航回转运动仿真预报分析

于东，周军伟，李金华，桂洪斌，王威

(1.哈尔滨工业大学（威海）海洋工程学院，山东 威海，264209；2.齐鲁工业大学（山东省科学院）山东省科学院海洋仪器仪表研究所，山东 青岛，266061)

操纵性是影响船舶航运安全的一个至关重要的因素，三体船作为一种新兴的且船体结构有别于传统船型的船舶，对其操纵性进行研究十分必要［1-2］。三体船的研究最早开始于20世纪60年代，但最初并没有受到足够的重视，直到20 世纪80 年代末，英国率先在三体船研究领域中取得了一定的成果［3-4］，而后人们才开始慢慢重视对它的研究。直至今日，三体船由于其较好的稳性、耐波性与快速性，较大的甲板面积以及较强的生存能力等优势［5］，其在军用、民用领域中都占有了一定的地位，如英国的“海神”号军用试验舰、美国的“独立”号濒海战斗舰［6］、中国的“东救335”和“北救143”号救援护卫舰、英国的“埃比尼则·斯克鲁奇”号渡轮、法国的“海上协和”号三体渡船等均是其中的杰出代表［7］。

三体船由于其本身所具备的一些优点，已受到了人们的广泛关注与应用，但是目前对于三体船的大多数研究还集中在其快速性及耐波性方面［8-9］。三体船由于其3 个片体的存在，水下部分的总宽度较同等排水量的普通船舶要大得多，这使得其操纵性能较其他船舶也更为复杂，其片体在水下由于操纵问题而产生事故的概率也会较其他船舶高得多，因此对三体船操纵性进行研究也是目前三体船研究领域当中一个较为紧迫的课题［10-11］。

当前，预报船舶操纵性常用数离模型方程 组（mathematical model group，MMG）模型法，但利用MMG 模型预报船舶操纵性时需提前得到船舶的水动力导数［12］，而船舶水动力导数主要可通过3 种方法获得：1）经验图表（公式）法，该方法相对较为简单、易理解，且获得水动力导数的速度相对较快，但所得水动力导数的精度较差，不利于较为精确地预估船舶操纵性；2）约束模试验法，该方法所得水动力导数精度相对较高，但其成本亦相对较高；3）约束模数值仿真法［13-14］，该方法成本相对较低，所得水动力导数的精度较经验图表法亦相对较高，但是需对数十个约束模工况进行模拟，所耗时间亦相对较长，且根据MMG 模型所得船舶操纵性参数仅为船模在平面内的轨迹参数，缺乏对升沉、横摇、纵摇等相关响应参数的影响分析，而采用自航运动模拟方法不仅能够节省约束模仿真时间、大量计算工况所需的时间，同时还能够进一步得到船舶运动过程中的升沉、横摇、纵摇等相关运动响应参数，从而更加全面地分析船舶操纵性能［15］。

本文采用计算域随船体共同运动的方法，利用商用计算流体力学软件Star-CCM+对某三体船的自航回转运动进行了数值模拟，而后将模拟结果与基于MMG 模型法的约束模仿真结果进行对比，分析了所提三体船操纵性自航回转运动模拟方法的可靠性，预报了三体船的回转性能。

1 模型建立及网格划分

1.1 三体船计算模型

模拟所用的三体船是根据一艘实用三体船通过一定缩尺比缩小所得到的，其船长为3.273 m，主体型宽为0.793 m，吃水为0.119 m，其片体间距为0.32 m。模型采用大型通用有限元分析软件ANSYS 的工程制造集成计算（integrated computational engineering and manufacturing，ICEM）软件建立，其坐标系为：以船艉指向船艏的方向为x轴的正方向；以船舶中心位置指向左舷的方向为y轴的正方向；以重力的反方向为z轴的正方向。最终所建立的三体船模型如图1所示。

图1 三体船计算模型Fig.1 Compution model of trimaran

1.2 计算域的建立与网格划分

船模计算时的控制域采用长方体区域，沿x轴方向从船艏向正向延伸1 倍船长，从船艉向负向延伸3倍船长，沿y轴从船模的中纵剖面分别向两侧延伸1.5 倍船长，沿z轴从船模的水线面向正向延伸0.3 倍船长，向负向延伸1.5 倍船长。计算域网格的划分采用多块结构化网格，并在细化网格时需对计算域沿船体纵向、横向及切向的网格均进行加密，且靠近船体部分网格密度较大，远离船体部分的网格节点分布系数1.1～1.3，采用等比例渐进的形式逐渐稀疏，既能够保证计算的精度又能够提高计算时的效率。

计算域网格具体划分时通过改变各块区域上的网格节点数来调节网格尺寸，从而达到控制网格数量的目的。而计算域的网格尺寸，尤其是船体表面的网格尺寸对于数值模拟结果可能会产生一定影响，因此为减小网格尺寸对于计算结果的影响，同时保证计算效率，根据船模表面网格的尺寸不同设计了4款网格划分方案并分别对其进行自航回转运动数值模拟，以此来分析网格对计算精度和收敛性的影响，从而确定一款最优的网格划分方案。其中方案1 的船体表面最大网格尺寸为0.042 m，约为13‰船长；方案2 的船体表面最大网格尺寸为0.035 m，约为10.5‰船长；方案3 的船体表面最大网格尺寸为0.03 m，约为9.1‰船长；方案4 的船体表面最大网格尺寸为0.026 m、约为7.9‰船长。

基于以上4 种网格划分方案对船模在初始航速1.683 6 m/s，满舵角下的自航回转运动进行数值模拟，所得回转轨迹如图2所示，相关操纵性回转性能要素值见表1。从图2 中可以看出：方案3 与方案4的回转轨迹几乎完全重合，方案1 与方案3、方案4的回转轨迹相差较大，方案2 与方案3、方案4 的回转轨迹亦有一定的差别，从表1 中不同网格方案模拟时的船模回转性能要素表也可看出：基于方案3和方案4 的船模回转性能要素值极为接近，而基于方案1 和方案2 模拟得到的船模回转性能要素值相较于方案3 和方案4 的结果有一定的差别。综合考虑数值模拟时的计算精度以及计算效率，采用方案3的网格划分方式对船模进行数值模拟仿真。

表1 不同网格方案时的船模回转性能要素Table 1 Slewing performance factors of the model when the domain adopts different grid division schemes

图2 不同网格方案时的船模回转运动轨迹Fig.2 Slewing motion trajectories of the model when the domain adopts different grid division schemes

最终数值模拟采用的网格划分方案中，船体表面最大网格尺寸约为0.03 m，同时由于船艏部分曲率变化相对较大，因此对船艏区域进行了网格加密，加密后的船艏表面网格最小约为0.015 m。计算域网格划分情况见图3。

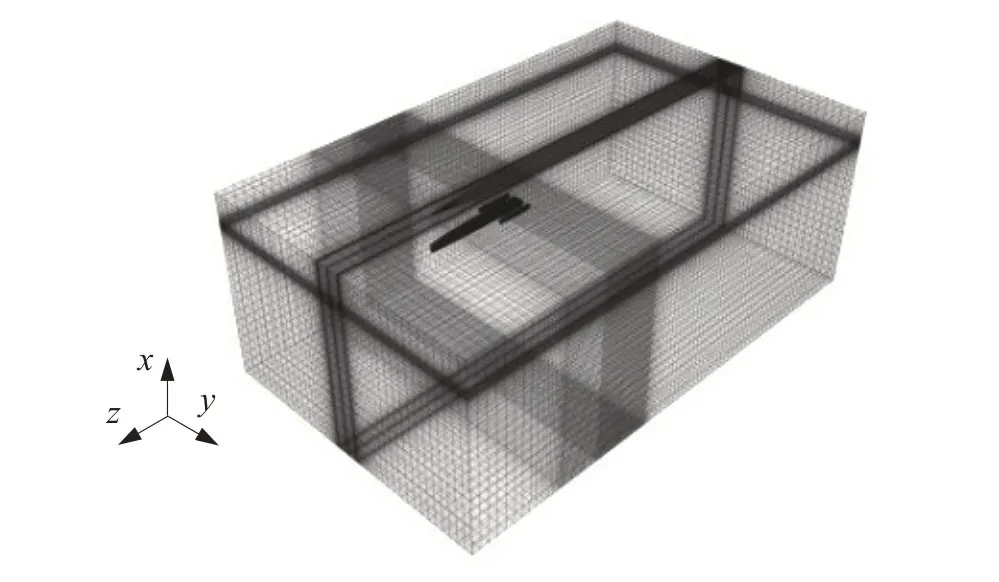
图3 计算域网格划分Fig.3 Grids of the domain

2 模拟方法及可靠性验证方法

2.1 数值模拟方法

本文在进行数值模拟时参考MMG 模型的思想，将船和推力部分分开考虑，首先分析出船体所受推力的情况，而后在商用CFD 软件star-CCM+中的DFBI模块中，将推力施加在船体上。采用这一方法对船模自航回转运动进行数值模拟时能够巧妙地避免由于船舶动力系统流场模拟所导致的计算网格数目过大，对计算能力要求过高以及计算效率较低等问题。文中模拟所用三体船是根据一艘实用三体船缩尺而得，该船在实际当中采用的是喷水推进器，该推进器给予船体的推力计算为：

式中：船模在稳定直航时的推力与阻力相等，因此X(u0)为船模以初始航速u0稳定直航时的阻力值；δ为喷水角；la为推力作用点距船舶重心的距离。喷水推进器相当于是桨舵的组合体，其通过改变喷水角来为船舶提供转向动力，本文亦借助满舵角、半舵角等相关思想对船模的回转运动进行分析，因此为方便分析和理解，将喷水角δ等价为舵角。

在对船模自航回转运动进行数值模拟时采取计算域随船模一起运动的方案，计算域的边界条件为：船体表面采用壁面边界条件，船艏所对应的计算域边界采用速度入口条件，船艉所对应的计算域边界采用压力出口条件，计算域的上下左右四周采用速度入口条件。数值模拟时采用剪切应力输运 (shear stress transport，SST)k-ω湍流模型，对流项采用一阶迎风格式进行差分，自由液面采用流体体积（vol‐ume of fluid，VOF）法进行捕捉，船模在运动时其在纵向、横向和垂向3 个方向上的位移和旋转均是自由的。

2.2 可靠性验证方法

根据MMG 模型预报船舶的回转轨迹和性能要素是船舶操纵性预报领域中较为常用也较为成熟的方法，因此本文将以基于MMG 模型方法的约束模数值仿真结果作为参照，将其与以上提到的三体船操纵性自航模拟方法所得结果进行对比分析，以验证文中所提自航模拟方法的可靠性。

基于MMG 模型的约束模仿真计算方法需建立三体船操纵运动方程，根据MMG模型建立方程为［8］：

式中：m为船舶质量；mx和my分别为船舶在x和y方向的附加质量；Izz、Jzz分别为船绕z轴的转动惯量和附加转动惯量；u和v分别为船舶在x和y方向的速度；r为船舶绕z轴的转艏角速度。

将式(1)中船体的粘性类流体动力及力矩用泰勒级数展开为：

根据式(2)船体动力学方程设计三体船悬臂实验的模拟工况为：u=1.683 6 m/s，β=-15o、-10o、-5o、0o、5o、10o及15o，r'=-0.3、-0.2、-0.1、0、0.1、0.2 及0.3。其中u为根据船舶的设计航速换算出的船模设计航速，β为漂角，即船艏方向与船模实际运动方向的夹角，r'为转艏角速度r的无量纲化值为船模的实际速度，V=u/cosβ，L为船长。

根据以上工况模拟船模的悬臂实验，采用最小二乘法对三体船的水动力进行拟合，求出其水动力导数，根据其水动力导数编写程序求出船舶的回转运动轨迹。

3 回转运动结果分析及对比验证

根据自航回转运动模拟方法和基于MMG 模型及约束模水动力导数的回转运动仿真方法，分别对船模在15o舵角及30o舵角下进行操纵性自航模拟及悬臂实验模拟，将结果进行对比，分析自航模拟方法的可靠性。

3.1 悬臂实验结果

根据以上确定的模拟工况，对三体船模的悬臂实验进行数值模拟。

其中当r'=0 时，船模的转艏角速度r=0 rad/s，此时船模的实际运动轨迹是一条直线，但是其船艏与运动方向存在着夹角β，因此此时船模是做斜拖运动，其结果见表2。

表2 斜拖运动水动力Table 2 Hydrodynamics of oblique motion

根据船模斜拖运动时的受力情况拟合出的其位置导数见表3。

表3 位置导数Table 3 Position derivatives

当β=0 时，船模的横向速度v=0，此时船模的合速度V=u，当r'不为0 时，船模是绕着一点做回转运动，而纵向速度u为回转运动的切向速度，此时船模所做的约束运动为无漂角悬臂运动，而当β=0且r'=0时，船模做的是直线运动。船模的无漂角悬臂运动数值模拟得到的水动力值见表4。

表4 无漂角悬臂运动水动力Table 4 Hydrodynamics of no drift angle rotating arm

根据船模的无漂角悬臂运动数值模拟结果，采用最小二乘法拟合出的船模旋转水动力导数值见表5。

表5 旋转水动力导数值Table 5 Rotating hydrodynamic derivatives

当β≠0 且r'≠0 时，船模做带漂角悬臂运动，此时通过模拟得出船模水动力值见表6。

表6 带漂角悬臂运动时的水动力Table 6 Numerical simulation results of rotating arm with drift angle

根据表6 中船模带漂角悬臂运动时的水动力值拟合出的耦合水动力导数值见表7。

表7 船模的耦合水动力导数Table 7 Coupling hydrodynamic derivatives

船模进行约束模数值模拟时的自由液面波形见图4。根据约束模数值仿真结果得到的船体水动力导数，结合之前建立的三体船操纵性运动方程，采用四阶龙格库塔法，利用VB（visual basic）语言进行编程，仿真得到文中模拟的三体船在15°舵角及30°舵角时的回转运动轨迹见图5。

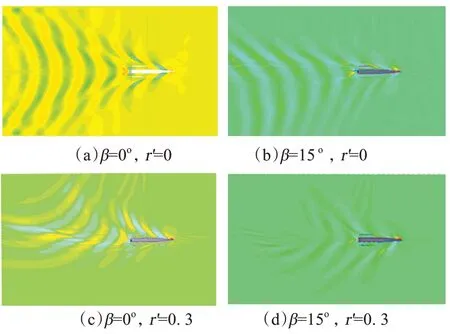
图4 约束模数值模拟自由液面Fig.4 Oscillogram of constraint dodule’s numerical simu‐lation

图5 30°及15°舵角下的回转运动轨迹Fig.5 Trajectory of rotary motion when the rudder angle is 15° and 30°

通过对以上船模回转运动轨迹进行分析，得出三体船在30°舵角及15°舵角下的操纵性要素见表8。

表8 根据约束方法得到的三体船操纵性要素值表Table 8 Maneuverability of essential factor of trimanran according on the constraint module’s method

3.2 自航模拟结果

3.2.1 自航回转运动轨迹

根据2.1 节中介绍的船模自航模拟方法对三体船模型在30°舵角及15°舵角下的回转运动进行数值模拟，自航模拟过程中船模不同时刻的自由液面波形图见图6，根据模拟结果绘制船模的回转运动轨迹见图7。

图6 30O舵角下做回转运动时的自由液面波形Fig.6 Oscillogram of self-propelled motion when the rudder angle is 30°

图7 船模自航回转运动轨迹Fig.7 Trajectory of rotary motion when the model is self-propelled motion

通过对以上三体船操纵性自航回转运动结果进行分析，求得的船模操纵性要素值见表9。

表9 自航回转运动模拟得到的三体船操纵性要素值Table 9 Maneuverability of essential factor according on trimanran self-propelled rotating motion

根据对以上自航回转运动进行数值模拟得到的操纵性要素值进行分析可知，15°舵角下的船模回转直径明显比30°舵角下的船模回转直径大，15°舵角下的回转直径约为30O舵角下回转直径的173.86%，这一结果与船舶回转运动的统计规律也是相符的，根据实验统计，船舶在半舵角下的回转直径通常是其全舵角下回转直径的150%～180%，而本船的计算结果也恰好在该范围之内。因此可初步认定本文所提出的模拟方法相对可靠。

3.2.2 船舶转艏角速度

船舶在初始航速1.683 6 m/s，30°及15°舵角下做回转运动时其转艏角速度变化曲线见图8。

图8 船模自航回转运动时的转艏角速度Fig.8 Turning angular velocity when the model is self-propelled motion

通过图7、图8 可以看出，船模在做回转运动时其转艏角速度先增大而后渐渐趋于稳定。本文模拟的船模在30°舵角下回转时的转艏角速度约为0.18 rad/s，在15°舵角下回转时其转艏角速度约为0.128 rad/s。船模的转艏角速度与其回转一周所用的时间成反比关系，船模的转艏角速度越大其回转一周所用的时间越少，当船模的转艏角速度为0.18 rad/s 时，其回转一周大约需要35 s，加上船模刚开始做回转运动时转艏角速度存在着一个增加段，因此当船模以30°舵角做回转运动时，其回转一圈所用的时间约为40 s；同样，船模以15°舵角做回转运动时，其所用时间约为55 s。

3.2.3 船舶速降

船模在不同舵角下做回转运动时其速度的实时曲线见图9。从图9 可以看出，船舶在做回转运动时，其航速会先下降而后趋于一个稳定的值，这一现象即是船舶的速降。同时可知，船模以30°舵角做回转运动时，其航速最终稳定在1.11 m/s 左右，以15°舵角做回转运动时，其航速最终稳定在1.38 m/s左右，由此可知船模在30°舵角下回转时的速降为0.573 6 m/s，15°舵角下回转时的速降为0.303 6 m/s，其速降幅度分别为34.07%和18.03%。根据中国航海学会海洋船舶驾驶专业委员会统计，船舶在满舵角下做回转运动时，其速降幅度通常在25%～40%，本船速降幅度为34.07%，恰在此范围之内。

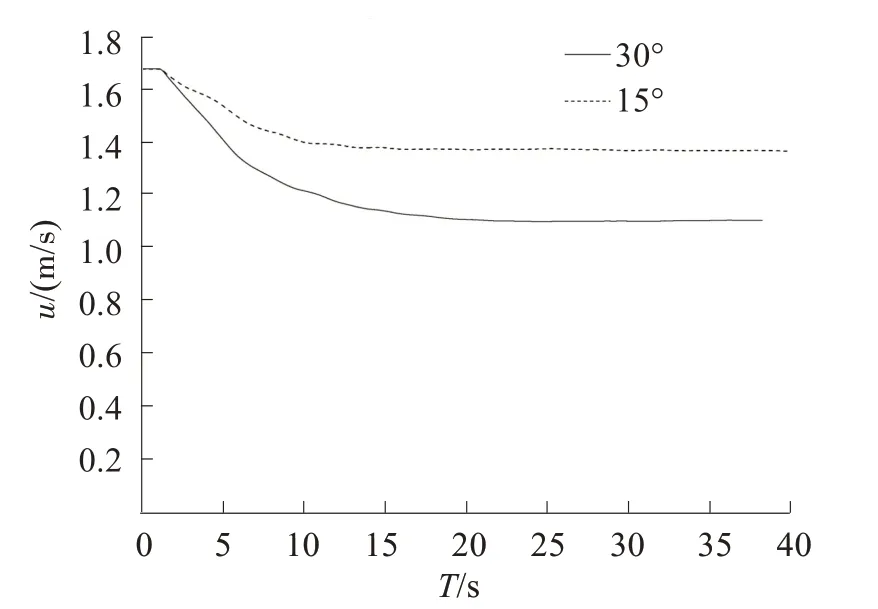
图9 船模自航回转运动时的速降Fig.9 Speed decline when the model is self-propelled motion

3.2.4 船模重心升沉运动轨迹

船模在初始航速1.683 6 m/s，舵角30°和15°回转时的重心升沉轨迹见图10。

图10 船舶自航回转运动时的升沉曲线Fig.10 The heaving when the model is self-propelled motion

从图10 可知，船模重心随着其回转运动的开始先产生相对剧烈的变化，而后随着运动的继续其重心升沉轨迹慢慢趋于稳定。这与之前探讨的船模回转运动的现象也是较为相符的，船模刚开始做回转运动时，船模的运动状态在剧烈变化，其航速、转艏角速度等均在发生变化，而随着其转艏角速度及航速等恢复到稳定的阶段，其回转运动也进入到一个稳定的阶段，近似于一个匀速圆周运动，因此此时船模的重心升沉轨迹趋于稳定。

3.2.5 船舶回转运动时的纵倾角

船模在不同舵角下做自航回转运动时其纵倾角的实时曲线见图11。从图11可以看出，船模在做回转运动时，其纵倾规律与其重心升沉规律较为相似，均是在运动的初始阶段变化幅度较大，而后慢慢趋于稳定，同时可知，船模以30O舵角做回转运动时其纵倾角是艉倾0.136°，船模以15O舵角做回转运动时其纵倾角是艉倾0.129O。

图11 船舶回转运动时的纵倾角变化曲线Fig.11 The teim when the model is self-propelled motion

3.2.6 船舶回转运动时的横倾角

船模在做自航回转运动时的横倾实时曲线见图12。船模在做稳定的回转运动时由于离心力的作用会产生一定幅度的内倾。根据图12 可以看出船模在静水中做回转运动时其产生了一定程度的橫倾且横倾角为负值，根据船体坐标系方向及船舶运动的方向可知，橫倾值为负值时船舶产生的是左倾，即内倾。船模在30O舵角下做回转运动时，其横倾角为0.60O，船模在15O舵角下做回转运动时，其横倾角为0.49O，二者之间的比值为1.22，根据船模回转运动时得到的半径值及角速度值，可推算二者之间的离心力比值约为1.14，这2 个值之间相差较小，这可以说明模拟结果与理论分析较为吻合，从这一点也可以间接证明本文方法的可靠性。

图12 船舶自航回转时的横摇历时曲线Fig.12 Rolling when the model is self-propelled motion

3.3 对比分析

由以上三体船模型的约束模回转运动轨迹与自航模回转运动轨迹可知，二者的回转运动轨迹在形状方面是较为相似的，因此对其回转运动时的各操纵性要素值进行对比分析，如表10所示。

表10 船模回转运动时的操纵性要素值对比Table 10 Maneuverability of essential factor of the model turning motion

根据表10 可以看出，30°及15°舵角下约束模回转要素值与自航模回转要素值之间均比较接近，2种计算方法之间各要素值的差别均在7%以内，由此可知，本文所提之操纵性自航模拟方法是较为可靠的。

通过对以上船模的2种预报方法进行分析可知，船模满舵角回转运动时的旋回初径D与其长度L之间的比值分别为3.86和4.1。根据试验统计，船舶在满舵角下的回转直径D与船长L之间的比值等于3，即D/L=3时，船舶的回转性能是较好的，而D/L=10时则认为船舶的回转性能是较差的，一般船舶的D/L值是在（5，7）内，由此可见本文所预报的船舶回转性能是比较不错的。

4 结论

1）文中所提出的三体船自航回转运动数值模拟方法是可靠的。

2）采用自航回转运动数值模拟方法预报三体船的回转性能时，可同时对其回转过程中的横摇、升沉和纵倾等相关运动响应进行分析，能够更加全面地预报船舶做回转运动时的性能。

3）文中模拟所用三体船的回转性能较好。

本研究的未来发展方向将主要是研究自航回转运动数值模拟方法对于各类船型的适用性以及拓展实现如 Z 型运动等其他操纵性自航运动的数值模拟等。