基于三维水动力方法的三体船连接桥波浪载荷计算分析
赵春慧
(浙江海洋学院船舶与海洋工程学院,浙江舟山 316022)
基于三维水动力方法的三体船连接桥波浪载荷计算分析
赵春慧
(浙江海洋学院船舶与海洋工程学院,浙江舟山316022)
文章应用三维水动力分析方法进行三体船连接桥波浪诱导载荷的研究工作,建立三体船水动力分析面元模型,计算三体船在迎浪状态下零航速和中低航速运动响应,并与三体船拖曳水池模型试验结果进行对比,证明了此计算方法的可行性。通过计算,探讨了三体船连接桥波浪载荷随航速和浪向的变化规律及特点,并对连接桥的波浪诱导载荷量级进行了一定的分析,计算结果对于提高三体船耐波性能和加强三体船的强度校核有重要的参考价值。
三体船;三维水动力计算;连接桥;波浪载荷
近年来,三体排水型高性能船舶的研究引起人们的较大关注。三体船的结构设计的规范尚不成熟,基于波浪载荷预报的直接计算方法是一种合理设计三体船结构的方法。
由于世界上已建成的三体船极少,作为新船型,三体船的结构设计尚未成熟。在水动力性能和耐波性方面人们已经展开了许多研究。在作用于船舶上的所有基本载荷中,船体表面波动压力和波浪诱导的剖面剪力弯矩是在强度计算中要求取的最重要的外载荷。此外,三体船舶连接桥结构的波浪载荷可以引起连接桥甲板结构变形和疲劳问题,为了合理的对甲板桥结构进行设计,有必要对其遭遇的波浪载荷进行预报。因此,研究三体船波浪载荷并对其进行预报显得很有意义。
本文拟展开基于三维水动力方法进行水动力求解,在无限水深条件下,在频域内计算船舶在规则波中的水动力、运动响应及波浪载荷的研究工作。了解三体船波浪载荷响应函数和分布规律特点,为后续三体船性能预报提供依据。
1 计算模型的建立和湿表面网格的生成
1.1三体船模型建立
本文通过Fluent Gambit软件与AutoCAD软件的结合,利用两个通用软件几何图形处理的优势,可以直观地在型线图基础上生成模型并划分网格而不需要对型值进行直接处理,并且能够在图形界面上控制网格的属性,可以满足三维水动力计算的需要。
整船湿表面网格共有1 482个节点,1 440个单元。本文选取船型FA-1-A,主体与侧体位置如图所示:

图1 FA-1-A的主体和侧体的位置关系Fig.1 The position relations of FA-1-A between the main and side body

图2 三体船水线以下网格俯视图Fig.2 Vertical view of grid underwater

表1 船模主体和侧体主尺度Tab.1 Principal particulars of the trimaran
1.2船体湿表面网格划分
面元法仅对水线面以下部分进行计算,所以本文只需建立三体船水线以下部分模型并划分网格。但水下部分仍然视为一个刚体,从而按三体船模型整体进行水动力计算,这样保证了与实船的计算结果相符。
在本文中,对完整的三体船的主题和两个侧体划分了水动力网格。整个水动力面元的网格数目是1 442块。其中主体划分了966块,每个侧体划分了288块。

图3 三体船网格可视化Fig.3 Grid visualization of the trimaran
2 运动理论预报结果同试验结果的比较
基于三维势流理论,首先对三体船的六个自由度的运动进行了计算。将得到的垂荡和纵摇结果与试验结果进行了比较,以验证方法的适用性。模型试验所选取的船型为FA-1-A,拖曳水池模型试验航速选取傅汝德数Fn=0.2、0.35、0.5、0.667。
图4~11是三体船模FA-1-A在迎浪中的垂荡和纵摇幅值运动响应三维理论与模型试验结果的对比。从上面的比较结果可知,在中低航速下,三维势流理论方法能够有效的预报三体船在波浪中的运动响应,但在高速下,垂荡和纵摇理论预报结果中出现了峰值振荡现象,这是水动力计算中的“伪共振”现象造成的。

图4 垂荡幅值响应(Fn=0.2,β=180°)Fig.4 Heave amplitude(Fn=0.2,β=180°)

图5 纵摇幅值响应(Fn=0.2,β=180°)Fig.5 Pitch angle(Fn=0.2,β=180°)
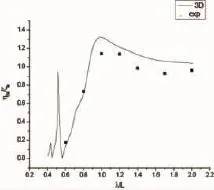
图6 垂荡幅值响应(Fn=0.35,β=180°)Fig.6 Heave amplitude(Fn=0.35,β=180°)

图7 纵摇幅值响应(Fn=0.35,β=180°)Fig.7 Pitch angle(Fn=0.35,β=180°)

图8 垂荡幅值响应(Fn=0.5,β=180°)Fig.8 Heave amplitude(Fn=0.5,β=180°)

图9 纵摇幅值响应(Fn=0.5,β=180°)Fig.9 Pitch angle(Fn=0.5,β=180°)
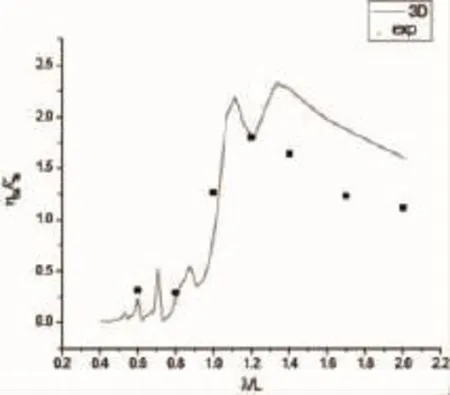
图10 垂荡幅值响应(Fn=0.667,β=180°)Fig.10 Heave amplitude(Fn=0.667,β=180°)

图11 纵摇幅值响应(Fn=0.667,β=180°)Fig.11 Pitch angle(Fn=0.667,β=180°)
3 三体船连接桥波浪载荷计算
计算中,选取连接桥中点处剖面作为参考,进行计算得到了剖面的纵摇弯矩、垂向弯矩、横向挤压力和垂向剪力。计算的航速选取为傅汝德数Fn=0,0.2,0.35,浪向角分别为30°、60°、90°、120°、150°、180°。以下图12~46为各弯矩、剪力随浪向和航速的变化情况。

图12 三体船连接桥纵摇弯矩My(Fn=0)Fig.12 Pitch moment My(Fn=0)

图13 三体船连接桥纵摇弯矩My(Fn=0.2)Fig.13 Pitch moment My(Fn= 0.2)

图14 三体船连接桥纵摇弯矩My (Fn=0.35)Fig.14 Pitch moment My(Fn=0.35)

图15 三体船连接桥垂向弯矩Mx (Fn=0)Fig.15 Vertical moment My(Fn=0)

图16 三体船连接桥垂向弯矩Mx(Fn=0.2)Fig.16 Vertical moment My(Fn=0.2)

图17 三体船连接桥垂向弯矩Mx (Fn=0.35)Fig.17 Vertical moment My(Fn=0.35)

图18 三体船连接桥横向挤压力Fy(Fn=0)Fig.18 Lateral extrusion pressure Fy(Fn=0)

图19 三体船连接桥横向挤压力Fy(Fn=0.2)Fig.19 Lateral extrusion pressure Fy(Fn=0.2)

图20 三体船连接桥横向挤压力Fy(Fn==0.35)Fig.20 Lateral extrusion pressure Fy(Fn==0.35)

图21 三体船连接桥垂向剪力Fz (Fn=0)Fig.21 Vertical shear Fz(Fn=0)

图22 三体船连接桥垂向剪力Fz(Fn=0.2)Fig.22 Vertical shear Fz(Fn=0.2)

图23 三体船连接桥垂向剪力Fz (Fn=0.35)Fig.23 Vertical shear Fz(Fn=0.35)
3.1浪向对连接桥波浪载荷的影响
通过计算结果可知,对于纵摇弯矩,在零航速时,60°和120°时有较大的峰值。在有航速时,120°~180°浪向下的幅值相对零航速有较大的增加,特别是在120°情况下,存在一个很大的峰值。
垂向弯矩的规律同纵摇弯矩,在有航速的情况下,120°~180°浪向下幅值相对零航速有较大增加,特别是在120°的情况下,存在一个很大的峰值。
对于连接桥间的横向挤压力,在零航速时,60°和120°时有较大的峰值。在有航速时,120°和150°浪向下的幅值相对零航速增加很多,特别是在120°情况下,存在一个很大的峰值。
对于连接桥垂向剪力,在零航速时,60°和120°对应有较大的峰值。在有航速时,120°~180°浪向下的幅值相对零航速有较大增加,特别是在120°情况下,存在一个很大的峰值。120°和150°时对应的载荷峰值和零航速相比发生了较大的变化。

图24 三体船连接桥垂向剪力Fz (β=30°)Fig.24 Vertical shear Fz(β=30°)

图25 三体船连接桥垂向剪力Fz (β=60°)Fig.25 Vertical shear Fz(β=60°)

图26 三体船连接桥垂向剪力Fz(β=90°)Fig.26 Vertical shear Fz(β=90°)

图27 三体船连接桥垂向剪力Fz (β=120°)Fig.27 Vertical shear Fz(β=120°)

图28 三体船连接桥垂向剪力Fz (β=150°)Fig.28 Vertical shear Fz(β=150°)

图29 三体船连接桥垂向剪力Fz (β=180°)Fig.29 Vertical shear Fz(β=180°)

图30 三体船连接桥纵摇弯矩My (β=30°)Fig.30 Pitch moment My(β=30°)

图31 三体船连接桥纵摇弯矩My (β=60°)Fig.31 Pitch moment My(β=60°)

图32 三体船连接桥纵摇弯矩My(β=90°)Fig.32 Pitch moment My(β=90°)

图33 三体船连接桥纵摇弯矩My(β=120°)Fig.33 Pitch moment My(β=90°)

图34 三体船连接桥纵摇弯矩My (β=150°)Fig.34 Pitch moment My(β=150°)

图35 三体船连接桥纵摇弯矩My(β=180°)Fig.35 Pitch moment My(β=180°)
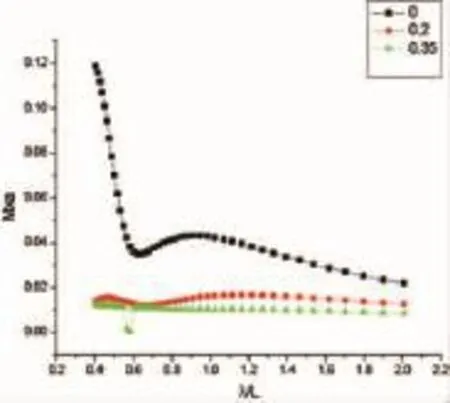
图36 三体船连接桥垂向弯矩Mx(β=30°)Fig.36 Vertical shear Mx(β=30°)

图37 三体船连接桥垂向弯矩Mx(β=60°)Fig.37 Vertical shear Mx(β=60°)

图38 三体船连接桥垂向弯矩Mx(β=90°)Fig.38 Vertical shear Mx(β=90°)

图39 三体船连接桥垂向弯矩Mx (β=120°)Fig.39 Vertical shear Mx(β=120°)

图40 三体船连接桥垂向弯矩Mx (β=150°)Fig.40 Vertical shear Mx(β=150°)

图41 三体船连接桥垂向弯矩Mx (β=180°)Fig.41 Vertical shear Mx(β=180°)
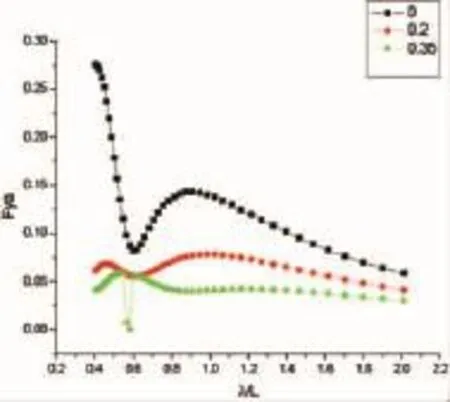
图42 三体船连接桥横向挤压力Fy(β=30°)Fig.42 Lateral extrusion pressure Fy(β=30°)

图43 三体船连接桥横向挤压力Fy(β=60°)Fig.43 Lateral extrusion pressure Fy(β=60°)

图44 三体船连接桥横向挤压力Fy(β=90°)Fig.44 Lateral extrusion pressure Fy(β=90°)

图45 三体船连接桥横向挤压力Fy(β=120°)Fig.45 Lateral extrusion pressure Fy(β=120°)

图46 三体船连接桥横向挤压力Fy(β=150°)Fig.46 Lateral extrusion pressure Fy(β=150°)

图47 三体船连接桥横向挤压力Fy(β=1800)Fig.47 Lateral extrusion pressure Fy(β=1800)
3.2航速对连接桥波浪载荷的影响
在90°(横浪)时,剪力和弯矩的幅值都不随航速的改变而变化。在0°~90°之间,剪力和弯矩的幅值都随着航速的增大而减小。在90°~180°之间,剪力和弯矩的幅值都随着航速的增大而增大。
航速较高时,运动响应中垂荡和横摇响应函数在为(0.4~0.8)之间,浪向角为120°和150°时较易出现峰值,对应的连接桥波浪载荷在这个区域内也发生这样的情况,这也说明由于运动出现的“伪共振”现象引起波浪载荷预报的不准确性。
在斜浪时,三体船连接桥载荷的变化较大,所以在船舶强度校核时,应充分考虑斜浪航行状态下剪力与弯矩的数量级。随航速的增加载荷变化很大,数量级变化也是很大的。所以考虑连接桥的载荷分布情况和数量级对船舶总强度的校核有重要的意义。
4 结语
本文建立了三体船模型,并划分了有利于应用于三维水动力计算的网格。通过计算可知三维势流理论能够有效的预报三体船在波浪中的运动响应,但在高速下,预报结果中存在峰值振荡现象,这是水动力计算中的“伪共振”造成的。应用这种方法来处理目前的多体高速船水动力计算,高航速下多体间水动力干扰效应没有考虑有航速下自由面波浪的三维波型效应,造成了片体间振荡兴波的堵塞和干扰,产生水动力计算的虚假共振。水动力计算上的伪共振对最终的运动响应结果产生了影响,因此造成了目前在基于三维的水动力计算的结果中出现了多峰振荡的现象。且三维势流理论的伪共振均随着航速的增大,峰值变大,峰值位置向低频移动。本文的计算结果对于提高三体船耐波性能和加强三体船的强度校核有重要的参考价值。
[1]戴遗山.船舶在波浪中运动的频域与时域势流理论[M].北京:国防工业出版社,1998.
[2]魏跃峰.多体船纵向运动预报研究[D].哈尔滨:哈尔滨工程大学,2007.
[3]马山.高速船舶运动与波浪载荷计算的二维半理论研究[D].哈尔滨:哈尔滨工程大学,2005.
[4]李积德.船舶耐波性[M].北京:国防工业出版社,1981.
[5]卢晓平,郦云,董祖舜.高速三体船研究综述[J].海军工程大学学报,2005,17(2):44-52.
[6]黄晓琼,陈立,杨雄辉,等.三体船波浪诱导载荷计算研究[J].中国舰船研究,2008,3(5):16-20.
[7]李培勇,裘泳铭,顾敏童.高速三体船型概念设计研究[J].上海交通大学学报,2004,39(11):1 185-1 188.
[8]缪国平,刘应中,等.切片理论应用于双体船运动计算时的伪共振问题[J].中国造船,1997(2):32-38.
[9]吴帆行,刘见华,黄守成.三体船垂向波浪载荷预报[J].船舶,2008(6):13-18.
Research on Wave Loads of the Trimaran Cross Structure based on Three Dimensional Hydrodynamic Analysis
ZHAO Chun-hui
(School of Naval Architecture and Ocean Engineering,Zhejiang Ocean University,Zhoushan316022,China)
The research work of using three-dimensional hydrodynamic analysis to solve the wave load of trimaran cross structure is present in this paper.Establish the trimaran hydrodynamic analysis surface model and compute the motion response of the trimaran in head seas at zero speed and low-speed,and compared with the towing model test results to prove the feasibility of the calculation method.By calculation,discusses the variation and characteristics ofwave load on trimaran cross structure with speed and wave,and the cross structure wave loads order is also take into account,the results achieve for improving the trimaran seakeeping performance and strength check has an important reference value.
trimaran;three-dimensional hydrodynamic;cross structure;wave loads
TM619
A
1008-830X(2015)02-0151-07
2015-01-20
浙江省自然科学基金项目(LY14E090003)
赵春慧(1986-),女,浙江舟山人,助理实验师,硕士,研究方向:船舶耐波性.E-mail:13715657@qq.com

