仿生导流叶片管路降噪特性研究

王献忠，李宁，林鸿洲，叶栗栗，冯伟佳

(1.高性能船舶技术教育部重点实验室(武汉理工大学)，湖北 武汉 430063；2.武汉理工大学 交通学院，湖北 武汉 430063;3.中国船级社福州分社，福建 福州 350008)

管路系统是舰船中的重要部分，承担着运输水、油等流质的重要任务，并且覆盖广泛、种类繁多。弯管是管路系统中的常用部件，因为在水流过弯头处时，会产生较大的流噪声，所以很多学者对弯头处进行了改进，以此来抑制噪声的产生，较为常用的方法就是在弯头处添加导流叶片。Zhang 等［1］对安装导流叶片的弯管进行研究，分析了不同雷诺数下流动引起的振动与噪声，大涡模拟计算结果表明安装导流叶片后，弯管处的漩涡范围明显减少，并且有效减少了流噪声；魏杰证［2］通过对通气管路加装导流叶片进行分析，并且研究了不同位置处导流叶片的降噪效果，结果表明导流叶片可以防止气体在弯头处产生涡流，减少噪声产生，并且在弯管前部加装导流叶片效果要优于后部。

目前，仿生学已经逐步应用于飞机、列车、建筑等行业中，仿生技术已成为学者们研究的热点。代翠等［3］对离心泵叶片进行仿生设计，建立了具有V型沟槽的叶片模型进行研究，结果表明仿生叶片可以降低叶轮内部湍流度，改变涡结构，减小流道内声功率；Dai等［4］亦是对离心泵进行仿生研究，发现仿生凹坑可以有效地增加边界层厚度，减少壁面压力，具有减阻降噪的效果；仝帆［5］将航空发动机的叶片进行模仿猫头鹰尾缘锯齿结构设计，并开展了数值实验研究，结果表明尾缘锯齿结构可以在锯齿根部的边缘产生流向涡，抑制大尺度展现涡脱落，有着明显的降噪效果；Li等［6］将球形沟槽对气动噪声的影响进行了研究，研究表明球形沟槽减小了壁面脉动压力，延迟了边界层的分离有效地控制了气动噪声；胡利鸿［7］研究了不同织构表面对摩擦振动噪声的影响与机理，发现仿生织构表面可有效降低高频尖叫噪声。

根据上述文献研究可以知道，仿生设计是减阻降噪的重要方法，并应用于机翼、离心泵等设备，而对于管路的降噪研究并不多。本文将管路导流叶片设计与仿生技术相结合，研究二者交叉对管路流场和流噪声的影响，从而进一步探究管路减振降噪方法，对管路进行再优化设计。

1 大涡模拟模型和Lighthill声类比理论

1.1 LES模型

大涡模拟模型［8］（large eddy simnlation,LES）是计算非定常流动常用的湍流模型，大涡模拟方法通过滤波函数将大尺度涡和小尺度涡进行分离，大尺度涡通过N-S 方程直接求解，小尺度涡通过亚格子模型进行处理。滤波方程为：

式中：x′为实际流动区域中的空间坐标；x为滤波后的大尺度空间上的空间坐标；V为控制体积几何空间的大小。

经过滤波后大尺度涡的控制方程为：

式中τij为亚格子应力。

本文小尺度涡选择WALE 亚格子模型［9］处理，此模型采用速度梯度张量的平方，考虑了变形率张量和旋转张量，在近壁面尺度下得到较好的涡粘性，其公式为：

式中Cw为WALE模型常数，默认取0.5。其中：

1.2 Lighthill声类比理论

Lighthill 声类比理论［10］将声学问题进行简化，并将声源项分别表达出来。

Lighthill方程为：

频域下Lighthill方程式为：

可以得到式（9）的有限元公式为：

式（10）各项积分并使用高斯定理最终得到：

式中：右侧第1 项为壁面偶极子声源，第2 项为四极子声源。

2 计算模型构建

本文选择在弯头中心处添加导流叶片的弯管作为基准研究模型，弯管截面为直径D=85 mm 的圆形，进流段长度为L1=6D，去流段长度为L2=10D，弯头处曲率为R=1.25D，模型的原点位于入口截面圆心，弯管肘部导流叶片厚度为h=1 mm，位于弯头中间部分，将此管命名为原管。弯管模型及导流叶片位置示意如图1 所示。对导流叶片进行仿生设计，在导流叶片上表面流向方向上布置边长为0.8 mm的等边三角形沟槽，仿生设计后的导流叶片及沟槽型式、尺寸如图2所示，将此管命名为仿生管。

图1 弯管模型及导流叶片位置示意Fig.1 Schematic diagram of the elbow model and the posi‐tion of the guide vanes

图2 仿生导流叶片示意及沟槽型式Fig.2 Schematic diagram of bionic guide vane and groove type

3 网格无关性验证

为了能够精准捕捉管壁及导流叶片处流动数据，保证计算的准确性，需要对弯管壁面设置边界层及导流叶片位置处进行网格加密，这样会导致网格数增多，占用过大的计算资源，因此对计算域进行网格无关性验证，保证计算精度的同时，缩减计算时间。本文调节不同网格尺寸将原管及仿生管计算域网格分别划分3种不同数目的网格，并进行计算，结果如表1。可以看出在原管网格超过220万，仿生管网格超过221 万后，总声压级变化不超过1%，因此原管采用第2套网格，仿生管采用第3套网格。

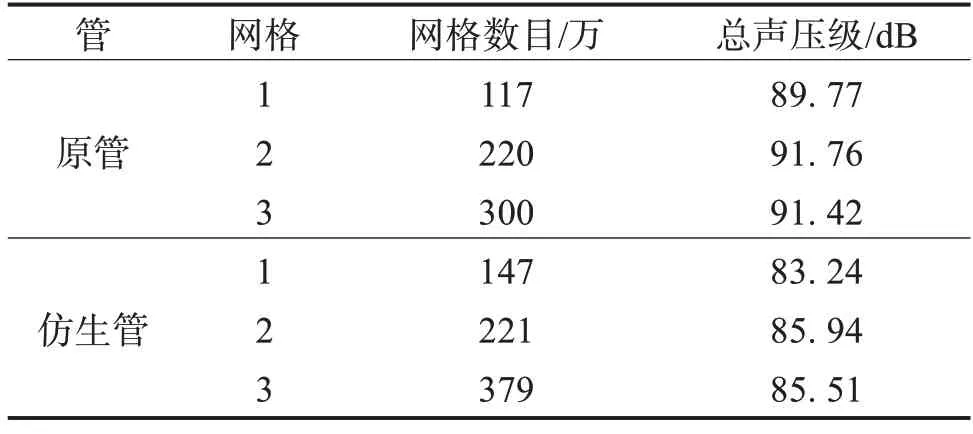
表1 原管与仿生管网格无关性验证Table 1 Verification of the independence of the original pipe grid and bionic pipe

4 计算方法有效性验证

本文的噪声计算采用LES/Lighthill的混合计算方法。为了验证计算方法的准确性和可靠性，本文基于水管路系统实验平台，设计了带导流叶片的弯管实验，并将实验测量结果与数值计算对比。

4.1 测试系统

本文实验由B&K 8104 水听器接收管内声压信号，通过电荷放大器、数据采集器传输，最后在计算机内处理声信号。本文实验水听器采用齐平式插入法，其固定基座内表面敷设吸声材料，测点位置布置在远离管路附件肘部10D的位置。实验用管路附件为DN80 的弯头，曲率半径R=1.25D，并在弯头中间位置焊接导流叶片，材质与管路材质一致，厚度为0.5 mm。试验示意如图3所示。

图3 测试系统示意和添加导流叶片的弯管Fig.3 Schematic diagram of the test system and the elbow with the guide vane

4.2 结果对比

在实验弯头安装结束后，调整阀门，使流入管路的流体保持3 m/s流速，待测试系统稳定后，进行噪声测试，测试频段为1 000 Hz以内。建立与实验模型一致的计算模型，并使用流体软件联合声学软件对其进行数值仿真，计算频段10～1 000 Hz，最终将实验结果与计算结果对比，如图4所示。图4可以看出实验结果曲线和计算结果曲线的整体趋势是一致的，实验数值在低频段略大于计算结果，一部分原因是受到背景噪声影响，另一部分原因是管路振动引起的低频噪声，会沿管路传播被水听器检测到。计算结果曲线在频率360、800 Hz 附近出现峰值，这是因为受到声学模态影响而出现峰值。总体可以看出实验结果与计算结果吻合较好，可以证明计算方法的可靠性。

图4 噪声实验与计算结果对比Fig.4 Comparison of experimental and calculated results for noise

5 流场计算

5.1 流场计算设置

本文对原管及仿生管进行流场计算，稳态计算时选择标准k-ε模型，基于速度-压力耦合求解，并且基于湍流强度和水力直径进行边界处湍流设定。导流叶片处及管路壁面设置为无滑移壁面。在稳态计算达到收敛后，再进行基于LES模型的瞬态计算。流场计算介质为常温下的水，密度ρ=1 000 kg/m3，对原管和仿生管分别进行2、3、4 m/s的流场计算。

流场计算的时间步长根据库朗数（courant num‐ber）进行估算，大涡模拟计算时一般取0.5～1，计算公式为：

式中：v为流速；Δt为时间步长；Δx为网格尺寸。

根据式（12）计算得到时间步长应小于10-3s，为了保证计算精度，实际采用的是10-4s。

5.2 网格划分

由于仿生设计后的导流叶片结构复杂，故本文的计算模型统一采用非结构化网格进行划分。为了精准捕捉管壁和导流叶片处的流场数据，对管壁设置边界层［11］，对导流叶片位置进行网格细化。第1层边界层设置时，为了适应LES 湍流模型，通常选择低y+值，使网格结点位于粘性底层范围内，可以使得过渡层和对数律层的涡可以直接求解，提高计算精度［12］，y+计算公式为：

式中：h为第1层网格到壁面的距离；μ为粘性系数；τ为流体切应力。

文本文选择y+值在1～20，第1 层边界层尺寸为3×10-5m，边界层的层间增长率为1.3，设置14层边界层，管口及导流叶片处网格划分如图5。管路与导流叶片位置处的壁面y+如图6所示，可以看出管路壁面y+值在1左右，导流叶片位置处y+值在15左右。

图5 入口及导流叶片处网格划分示意Fig.5 Schematic diagram of grid at the inlet and guide vanes

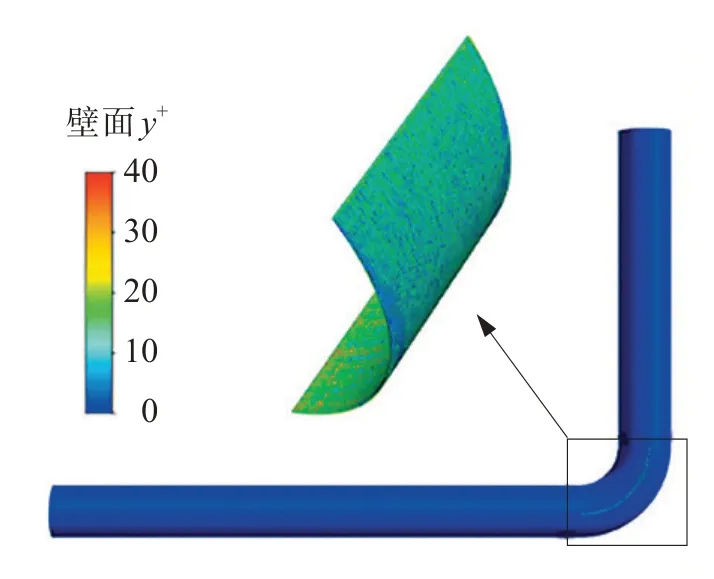
图6 弯管及导流叶片处壁面y+值Fig.6 The y+ value of the wall at the elbow and guide vane

5.3 流场分析

对计算域的流场数据进行可视化分析，以管路中剖面作为分析面，得到4 m/s流速下的速度云图如图7所示。导流叶片具有降噪作用是因为其导流作用，导流叶片将弯头处流场分为两部分，避免了大面积高速流体的聚集并直接冲击管壁，减少了涡的产生，从而起到降噪的作用；但是在导流叶片尾部会产生小范围不稳定的低速区域，并一直延续到管路出口；在对导流叶片仿生设计后，尾部的低速区域减少且更快地达到稳定，可以有效避免漩涡的产生。为了进一步分析流场情况，对管路中剖面方向的涡量进行表征为：

图7 分析面处速度云图Fig.7 Velocity cloud diagram at the analysis surface

对3 种流速的流场数据处理后，得到管路剖面方向的涡量云图，如图8。可以看出，在流体流过带导流叶片的管路时，主要在导流叶片尾部及内侧管壁产生涡，随着流速的增加，涡的范围和强度亦逐渐增大；当对导流叶片进行仿生设计后，导流叶片尾部及内侧管壁的涡强度及范围都明显降低，说明可以有效抑制涡的产生，这一点与前文所述对应；在2 m/s 流速下，仿生导流叶片对壁面涡的抑制最为明显。根据涡声理论［13］，低速流体下主要发生源是涡，因此在涡被抑制后，就会明显降低噪声的产生。

图8 不同流速下剖面方向涡量云图Fig.8 Vorticity cloud diagram in cross-section direction under different flow velocity

6 噪声计算

根据Lighthill 声类比理论可以得出，管路系统噪声源主要是壁面偶极子声源与四极子声源，其中对于低速流动，四极子声源可以忽略。在声学计算时，一般声学计算的最大网格尺寸应小于计算频率对应波长的1/6，即lmax＜c/6f，c为介质中声速，m/s；f为计算频率，Hz。本文计算频段为10～1 000 Hz，因此本文声学网格尺寸选择0.01 m，满足计算精度要求，然后基于边界元方法（boundary elementmethod,BEM）对管路噪声进行计算。

6.1 声模态计算

管路的声学模态振型特征用于分析某一频率下管路声压分布。为了分析管路流噪声频谱曲线特征，现对10～1 000 Hz频段内原管及仿生管的声学模态进行计算，计算结果如表2所示。表2可以看出导流叶片的仿生设计对管路声学模态影响不大。因为声学模态与管路流噪声计算结果相关，可以得出流噪声频谱曲线在500 Hz和1 000 Hz附近将出现峰值。

表2 管路10～1 000 Hz声学模态Table 2 Pipeline 10～1 000 Hz acoustic mode

6.2 噪声分析

对2、3、4 m/s 等3 种流速下的原管及仿生管的流场数据进行提取，导入声学软件并基于Lighthill声类比理论进行声源提取与转换，计算并对比原管与仿生管在频段10～1 000 Hz 下的流噪声，并在距离出口截面外50 mm 处设置监测点，最终计算结果如图9；并将管路总声压级进行对比，如表3。由图9、表3 可以看出，管路噪声能量主要集中于中低频段；在3种流速下，导流叶片的仿生设计对于管路降噪均有一定效果，总声压级分别降低7.05 dB、6.62 dB、3.71 dB，在流速2 m/s 时降噪效果最佳，并呈现出随流速增加而降噪效果减小的趋势；并且在频段10～300 Hz、500～900 Hz 内降噪效果最为明显；在频率500 Hz 与1 000 Hz 附近出现峰值，这是因为受到声学模态的影响，这与6.1节中得到的结论一致。

表3 不同流速下各管总声压级对比Table 3 Comparison of total sound pressure level of each tube at different flow rates dB

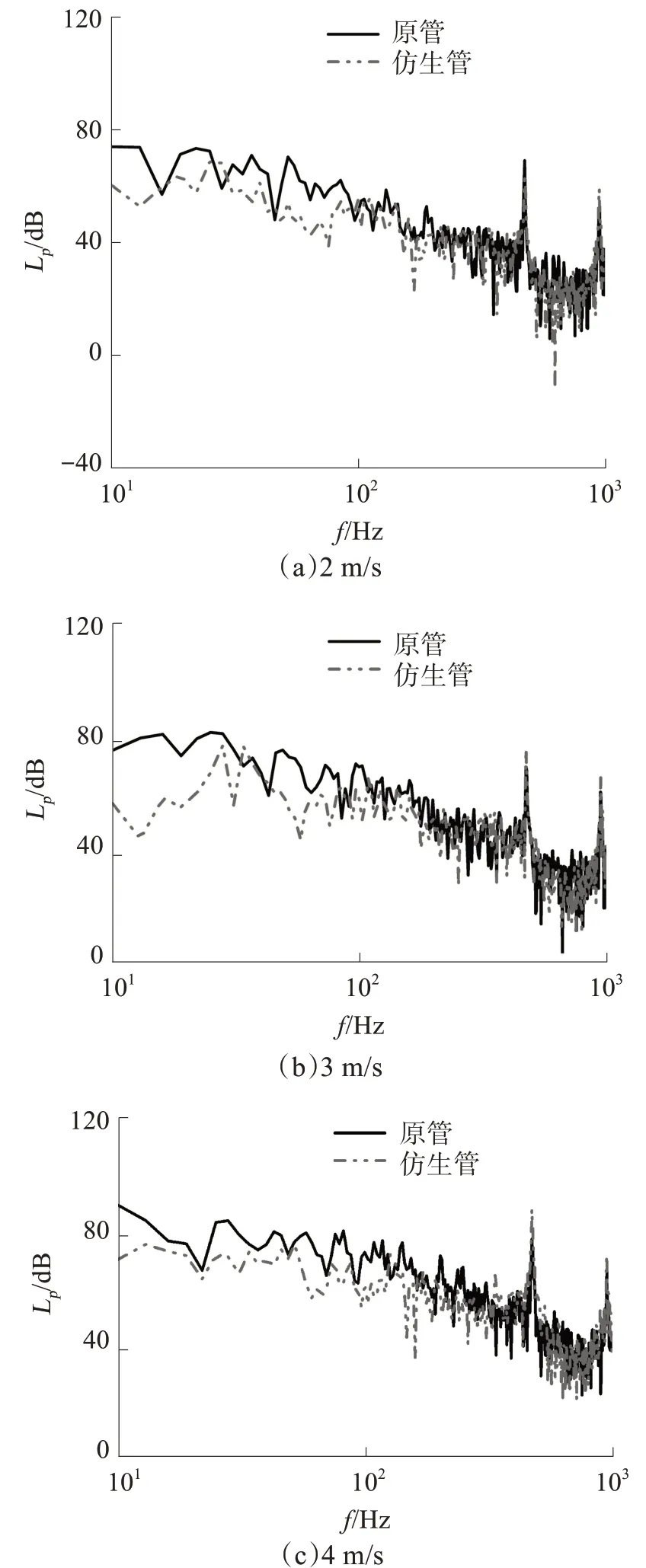
图9 不同流速下原管与仿生管声压级对比Fig.9 Comparison of sound pressure level between origi‐nal tube and bionic tube at different flow rates

为进一步分析3 种流速下仿生导流叶片的降噪特征，分别将3 种流速下原管与仿生管的声压级曲线进行计算为：

式中：LD为降噪值，LD＞0 时代表有降噪效果，否则代表无降噪效果；Lpre为原管声压级；Lbio为仿生管声压级。

根据计算，不同流速下降噪效果对比如图10所示。从图10 中可以直观看出，导流叶片的仿生设计并非在所有频段内都有降噪效果，在频段10～300 Hz、500～900 Hz 内有着明显降噪效果；在频段10～100 Hz内，3 m/s流速下的降噪效果最佳；在频段100～500 Hz 内，4 m/s 流速下的降噪效果最佳；在频段500～1 000 Hz 内，3 种流速下的降噪效果不相上下。但是，整体看来在2 m/s 下降噪效果最稳定，说明2 m/s流速下降噪效果受频率影响较小。

图10 3种流速下降噪效果对比Fig.10 Comparison of noise reduction effects of three flow rates

7 结论

1）导流叶片仿生设计可以有效抑制导流叶片尾部及管路内侧壁面涡的产生，从而减少噪声的产生。

2）在不同流速下，仿生导流叶片均可以减少管路噪声的产生，较低流速下的降噪效果最佳。

3）在3 种流速下，仿生导流叶片不同频段下的降噪效果各异，较低流速下降噪效果最稳定，受频率影响较小。