转子翼驱动功率与升/阻力特性研究

梁利华，姜寅令，2，史洪宇，李剑峰

（1.哈尔滨工程大学 智能科学与工程学院，黑龙江 哈尔滨 150001；2.东北石油大学 电气信息工程学院，黑龙江 大庆 163318）

马格纳斯（Magnus）减摇装置（转子翼）是一款新式的船舶减横摇装置，不同于传统减摇鳍的翅片形结构，它由一个快速旋转的圆柱体构成。传统翅片形减摇鳍主要利用形状效应来产生鳍表面的压力差，对航速依赖较大，低航速时无法产生足够的减摇力矩［1-2］。转子翼是利用圆柱体主动旋转诱导转子上下表面流体产生流速差，从而产生压力差，因此减摇效果受航行速度影响相对不大。转子翼在低航速船舶减摇方面表现出较优异的减摇性能。如由美国RiverHawk 公司建造的高级多任务平台（advancde nultitasking platform,AMP）、霍恩贝克离岸服务公司生产的潜艇支援舰、近海巡逻舰（offshore patrol ves‐sels,OPV）等采用了Magnus 减摇装置。目前，Mag‐nus 减摇装置只在RotorSwing 和Quntuam 公司有产品问世。RotorSwing 出品的MagnusSWING140 采用全电动伺服系统，一般适合小型船只使用，长度一般不超过30 m，最高航速可达26 kn，林森等超级游艇已成功安装使用且展示出较优异的减摇效果［3］。Quntuam 公司的MAGLiftTM系列产品采用液压驱动，适合较大型船只的低航速减摇要求［4］。

国内对低速主动式减摇装置的研究主要集中在零航速减摇鳍方面［5-7］。对Magnus 减摇装置的研究还处于起步阶段。文献［8］目前正积极投入低航速转子翼减摇装置的研发，基于Magnus效应的摆动旋转圆柱实验教学平台已搭建完成；梁利华等［9］发明了一种T 型Magnus 减摇装置。一款新型的减摇装置功耗问题也是行业关注的重点。本文主要研究转子翼的驱动功率并和传统减摇鳍进行对比，分析得出转子翼的功耗特点。

1 转子翼减摇机理

一对转子翼安装于船舷两侧，见图1 所示。当受风、浪等的影响产生如图1 所示横摇时，2 个转子翼转速大小相等方向相反，每半个周期改变旋转方向，从而产生扶正力矩。

流体中旋转圆柱的升力的产生可以用Kutta-Joukowski 定理来表示。流体流过任意形状的固定体，则单位长度上的升力可表示为［10］：

式中：ρ为流体密度；V为来流速度；环量Γ的定义为沿着一个包围固定体的封闭轮廓线C（顺时针方向）的曲线积分：

式中：被积函数Vcosθ是局部流体速度在曲线C切线方向上的分量；ds是曲线上的一个无限小长度。

若绕流圆柱体的环量是由圆柱体自身旋转引起的，则环量为［11］：

对于长度为Lm，转速为nr/min 的圆柱体上的升力为：

式中FL指向为来流方向逆环量方向旋转90°。升力会使物体发生横向运动，该现象被称为Magnus 效应，如踢足球的“香蕉球”现象。

对比NACA 翼型的升力正比于来流速度的平方，转子翼降低了对来流速度的依赖，低航速时可以通过加大转速达到减摇的目的。

2 三维转子翼几何模型及数值仿真

2.1 几何模型及数值验证

为了研究转子翼上的动态流体特性，采用AN‐SYS-FLUENT 对三维转子翼模型进行瞬态仿真研究。几何模型及流场设置见图2。转子放置到流场中心，左侧为速度入口V=7 kn，右侧为压力出口，其他矩形流场面设为对称面。L为转子翼长度，D为直径。圆柱转子壁面设为旋转动壁面，壁面运动由profile 文件写入。由于升力一般具有单峰特性，转子翼的运动包含加速（启动）、减速（制动）及匀速3个过程，一个横摇周期的转子翼转速变化曲线如图3（a）所示。K-ε模型是常用的湍流模型［12］，已经成为实际工程流计算中的主要工具。本文选择K-ε的标准模型，其最大的特点是高雷诺数，而转子翼的工况雷诺数达5.0 × 106，位于超临界雷诺区，符合K-ε模型的适用范围。仿真材料设置为12℃时海水。转子翼尺寸等相关参数描述见表1。

表1 转子翼参数列Table 1 Specifications for rotor wing

图2 转子翼几何模型及流场设置Fig.2 Geometric model and flow field settings of rotor wing

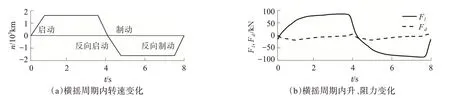
图3 横摇周期内转速及升/阻力动态变化Fig.3 Lift/drag vs.time in a rolling period

为了验证仿真数据的合理性，表2 给出转子翼不同航速下升力与实测结果、理论计算结果的对比。实测数据来自于Quantum 公司MAGLiftTM技术手册。本次仿真的转子尺寸介于2 款MAGLiftTM之间，若转速和航速相同的情况下，升力值应位于二者之间，从表2 可以看出，本文仿真结果满足该趋势，认为本次仿真具有合理性。实测数据和仿真结果均与理论计算数值有较大差异，这是由于Kutta-Jou‐kowski 定理是一种无粘理论，主要用来近似二维物体的升力。显然转子翼是有限长度的，考虑到能耗及船舶对附子的尺寸要求，目前市面上的转子翼长度一般不超过4 m，无法忽略三维效应，而且Kutta-Joukowski力的计算忽略了速度梯度，实际上对于粘性流体，边界层附近的速度梯度变化很大，因此实际上的转子翼升力与理论值将会产生不可忽视的差异。

表2 计算结果与实验结果、理论值比较Table 2 Experimental and numerical results compared to the present ones

2.2 升/阻力仿真结果及分析

图3（b）为一个横摇周期内，转子翼升/阻力随时间曲线。可以看出，在转子均速阶段，转子翼升力可达约80 kN，平均升阻比大于4，该值小于传统翅片形减摇鳍。

图4 为一个周期，动态升/阻力与转速的关系。可以看出，转子翼在加速阶段升力与转速近似成线性关系，升力正比于转速。本次仿真未出现失速情况。减速阶段由于流体惯性存在高压存续状态。

图4 升/阻力与转速变化的关系Fig.4 Lift/drag vs.rotary speed in a rolling period

图5、6 是转子翼单位面积阻力、升力与常规减摇鳍的对比，常规减摇鳍的实测数据采用静态和稳态的方法获得。从图5 可以看出，转子翼单位投影面积的阻力显然比翅片形减摇鳍大，但同样其单位投影面积上产生的升力也更多，见图6。实际上，在本例航速条件下，常规减摇鳍无法产生足够的升力，但是转子翼升力可达80 kN 以上。

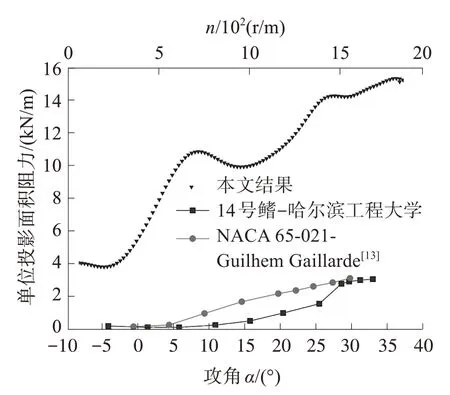
图5 单位投影面积阻力对比Fig.5 Comparison of the drag per unit projection area

图6 单位投影面积升力对比Fig.6 Comparison of the lift per unit projection area

不失一般性，横摇周期内不同时刻的压力云图、流线及涡流强度如图7、8 所示。通常的圆柱绕流试验都是通过改变来流速度或者圆柱尺寸从而改变雷诺数。本例中，虽然来流速度不变，但是圆柱附近的流体由于旋转运动的诱导，当转速变化时即相当于改变了流体速度，即增大或减小了雷诺数。从图7 可以看出，转子在起步加速阶段t=0.2 s，转速较小时流线分布均匀，随着转速增大，边界层流动变为湍流状态，t=2.2 s。要想获得足够的升力，转子翼应工作在高雷诺数的湍流状态t=2.2、5.2 s。图8（a）～（b）为航速7 kn 的转子翼压力云图，t=2.2、5.2 s 处于匀速状态，转速大小相等方向相反，因此产生的高压区位于转子相对的2个侧面，当t=4、8 s，转子处于换向的转折点，转速为零，不产生Magnus力，因此转子上的静压力以航行阻力为主，高压区均位于+z方向一侧。

图7 转子的压力云图、流速度线及涡流强度（t=2.2～8 s）Fig.7 Pressure contours,velocity streamlines and vorticities of the rotor swing（t=2.2～8 s）

图8 转子的压力云图Fig.8 Pressure contours of the rotor swing

航速显然会影响转子翼的升力和阻力，通常航速越高转子翼产生的升力越大，同时也伴随更高的阻力。图8（e）～（h）为航速12 kn 时的转子翼上压力云图，从高压区分布情况看t=6 s，转子翼高压侧没有7 kn时分布均匀，这是由尾部湍流更加紊乱引起的，因此可以推测，若继续增大航速转子翼将无法产生足够升力从而失速。

3 转子翼上力矩分析

3.1 摩擦力矩Mf

假设转子翼驱动轴有2 个支撑点，摩擦力矩为［15］：

式中fn、FMn、rn分别为转子第n个支承的摩擦系数、反作用力和驱动轴半径。在计算支撑处的反作用力时，可将鳍轴看作为具有2 点支撑的承受有集中载荷FM和均布载荷的外悬臂梁，见图9。集中载荷为转子翼上动态流体施加的力，即升力和阻力，均布载荷为转子翼重力与浮力，由于转子重力和浮力相当，计算时忽略此项。作用于转子翼的反作用力会随着动态流体力的变化而变化，呈周期性规律，前半个周期与后半个周期的摩擦力矩是相同的。

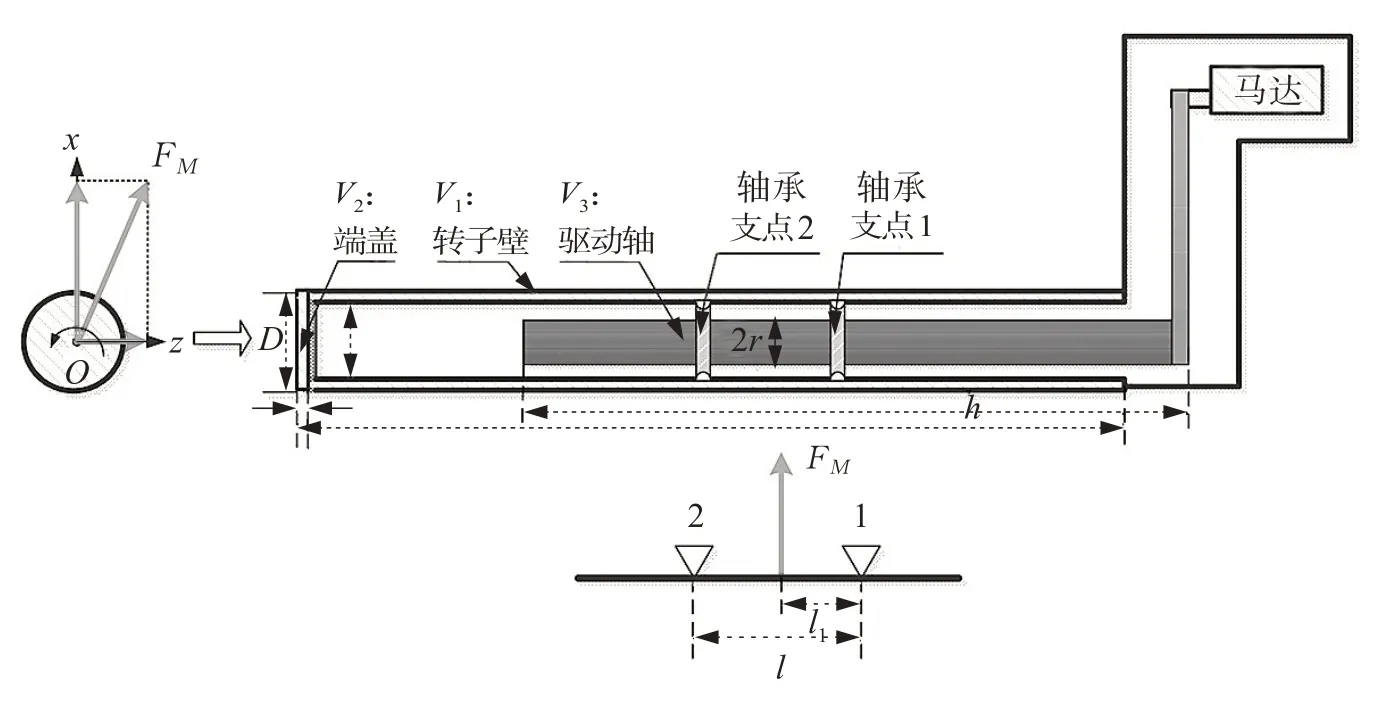
图9 转子翼简图及受力分析Fig.9 Sketch and force analysis of the rotor wing

3.2 惯性力矩ML

转子惯性力矩为：

式中：J为总的转动惯量，由圆柱面V1、端盖V2及驱动轴V3等3 部分组成；材料特性见表1，转子壁材料为碳纤维，驱动轴为17-4PH不锈钢；β为转子角加速度β=Δn/Δt。

3.3 粘滞阻力矩Mu

转子翼转子表面一般采用轻质、光滑表面材料构成［16］，粘滞阻力相对较小。计算海水对转子的粘滞阻力矩为［17］：

式中：f为流体对转子翼的摩擦系数；ASR为转子圆柱面积；VSR为转子圆柱表面速度；ASEPR为转子端盖面积；VSEPR为转子端盖表面速度。

3.4 转子翼驱动轴上的总力矩

驱动轴上的总力矩为摩擦力矩、负载力矩和粘滞阻力矩之和：

对于本例的转子翼，在船舶自然横摇周期8 s时，驱动轴上的最大总力矩Mmax=67.95N·m，平均总力矩为=23.77N·m，见图10。本例中，转子翼的支撑轴承应采用径向圆柱滚子超级轴承，摩擦力矩和粘滞阻力矩都比较小。总力矩集中在驱动轴部分的负载力矩上，因此转子翼的驱动轴应采用质量轻、刚度大的而材料。

图10 转子翼动态力矩与时间的关系Fig.10 Dynamic torque vs.time

根据在船模水池的鳍模水动力实验得到的原始数据，投影面积为3.2 m2的NACA00-15型减摇鳍，动态流体力矩均值达到13 000 N·m，最大总力矩为19 700 N·m。投影面积为0.9 m2的Weis-Fogh机构平均总力矩为9 876.8 N·m［15］。相比于翅片形减摇鳍，转子翼的总力矩、平均力矩更小，这也决定转子翼功耗相对较低。

4 转子翼伺服系统驱动功率

目前应用于减摇鳍液压系统的驱动功率计算主要采用定常的水动力［14］。本文采用动态水动力力矩代替定常水动力矩，一是转子翼上的水动力特性目前还未形成一个可靠的参考；二是采用动态水动力矩可以确定鳍上所受到的力矩变化，不会使所选的驱动功率过小而使转子翼失控，过大导致高功耗。常规减摇鳍的伺服系统主要采用液压驱动，而转子翼大多采用电动伺服系统。本节利用3.4 节的数据和方法来计算驱动功率。

描述电机的转轴的做功为：

式中用转矩（N·m）和转速（r/min）描述功率。则本例最大驱动功率为：

理论上额定功率为：

通过式（10）计算得出Nmax=11.39 kW，从图7可以看出，最大总力矩出现在转子翼启动和制动阶段，并不和最大角速度同时出现，因此按照式（10）计算的功率比较保守。通过式（11）计算得出额定功率NP=3.38 kW，若做功效率η=0.45（电力驱动一般取（0.4～0.5），则额定功率约为7.6 kW。对比98 m 船只的NACA0015 型减摇鳍，最大功率为24.931 kW，额定功率为8.68 kW［14］。本例中转子翼（适用船长80～100 m）驱动功率更低。

5 结论

1）在本文的研究条件下，转子翼平均升阻比达4，该值低于NACA00-15（δ=10°）减摇鳍，转子翼的航行阻力大，应寻求更好的减阻措施。

2）转子翼的惯性力矩在总力矩中占主导，摩擦力矩和粘滞阻力矩较小，寻找轻质高强度驱动轴材料是减小功耗的有效途径。

3）相比翅片形减摇鳍，转子翼的驱动功率更低，但航行阻力较大，总的能耗在高航速时较大，目前来看是一款低航速减摇设备。