“双减”背景下基于学科大概念提升课堂教学质量

赵让成

摘要：依托学科大概念优化小学数学课堂，能够达到高效节时的目的，为“双减”政策的落地助力。一是基于学科大概念进行教材梳理，为教学资源的优质筛选奠定基础。二是通过学情诊断，为提升课堂教学质量提供精准依据。三是基于学科大概念优化教学路径、方法，运用转化思想，提升课堂效益，提升学生的学习力与迁移力。本文以人教版小学数学五年级上册“小数除法”为例进行探析。

关键词：小数除法；学科大概念；梳理教材；诊断学情；创新教法

“双减”不是“减去”学生应有的学习负担，而是杜绝费时低效，倡导高效节时。基于学科大概念提升课堂教学质量，正是落实上述“拒绝”与“倡导”的措施之一。所谓“学科大概念”，是指能够将学科的关键内容及关键思想进行有机融合，建构成具有较强系统性学科框架的重要概念。这是上位的、核心的、具有统摄与整合意义的概念。基于学科大概念盘活教学资源、优化课堂教学，能够帮助学生“探究知识本质、建构知识关联、感悟思想方法”[1]。就小学数学教学而言，基于学科大概念统摄教学，能够避免碎片化学习，是对数学知识的整体把握与结构性合拢，是指向数学思想与方法的过程。就小数除法的教學而言，不能单一地从小数这一个知识点出发，而应把整数、小数、分数统摄在一起进行理解与设计。比如，“商不变的性质”适合于任何数（而不仅仅是小数），整数除法与小数除法的算理具有“一致性”等等，数的细分适用于多种运算，完全可以“用一根线串起珠子”。从这样的大概念出发，学生正视运算一致性，容易运用转化思想，做到前后勾连，整体理解，达到提质增效的学习目的。

一、梳理教材寻找支点

细心观察部分数学课堂，可以发现教师碎片化解读教材、单线条推进教学进程的现象仍然存在。表面看，教学环节够齐全；深处分析，没有紧扣学科上位概念，知识点之间缺乏有效关联与整体衔接，以致于前后出现“断层”现象。“双减”背景下，这种“零散割裂”的教学应该予以摒弃，基于学科大概念而梳理教材寻找支点成为必然。所谓“支点”，就是勾连知识点的核心概念，就是结构化指向———就小数除法的教学而言，能够贯通“整数、小数、分数”三大块，做到真正意义上的举一反三。

人教版小学五年级上册“小数除法”单元教材安排了五个例题，看似比较分散，类型较多，但从学科大概念出发，则不难发现其中的“联系点与一致性”。通过重新梳理，基于学科大概念，我们把五个例题整合为两个序列：“除数是整数的小数除法”和“除数是小数的小数除法”。

这样的梳理与整合并非随意而为，而是关联性的结构重建，而且做到了由此及彼，螺旋上升———前者为后者奠定基础，后者通过变换形式印证前者，正所谓：“厘清小数除法的算理，是贯通整数除法和小数除法的支点”[2]。这样的盘活，就“双减”而言，有利于学生学习负担的减轻；从知识内在的机理而言，有利于知识树的形成，有利于实现运算的一致性，达到事半功倍的效果。

二、分析学情找准切入点

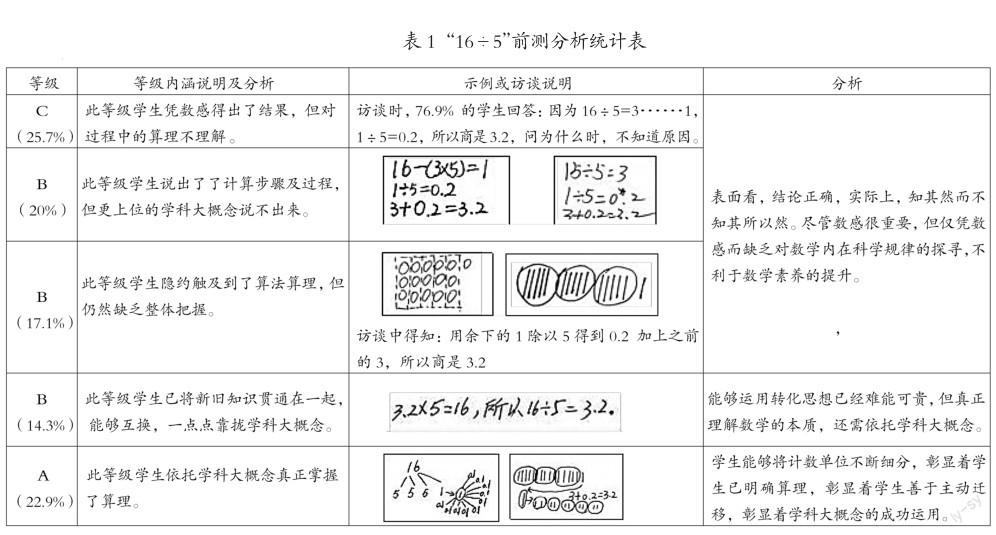
基于学科大概念开发课堂优质资源必须基于学生的真实学情，教师必须了解学生的学习起点与前知识结构，如此才能为精准教学与减负课堂的打造奠定基础。我们用算式“16÷5”为例进行前测（见表1）。

从表1中可以看出，课堂的费时低效源于碎片化学习———未能在前后知识的联结处进行有效关联，未能以上位或核心概念去整合算理，未能从迁移的角度去内化知识与方法。鉴于此，教师应基于学科大概念，重构教学框架，倡导整体教育观，通过转化思想优化教学过程，实现真正意义上的减负增效。

三、教学实践过程

（一）注重迁移，感受认知冲突

“16÷5”的结果不是整数，肯定有余数。如何表示这个带有余数的结果？我们引领学生从口答的整数除法入手，为小数除法算理的引出与总结做铺垫，进行知识脉络的续接，为基于学科大概念的课堂教学奠定基础。

组织学生口算16÷5与9÷4，其结论为“3……1”与“2……1”。教师追问：答案中的“1”如何理解？能否继续细分？“1”前面的长串省略号能否有更好的表达方式？个别学生的答案中有小数，带有省略号的表示形式是否可以用小数表示？

仅仅是一个口算环节，却将整数除法与小数除法联结到一起。可见，教师要有强烈的资源整合意识，要善于将新旧知识整合，善于引领学生通过溯源性思考，运用“连线串珠”的方法，明晰新旧知识的联系点与迁移点，实现学习效益的最大化。

（二）多元表征，体会算理本质

余数中的“1”与“0”始终是小数除法中的关键因子———相当一部分学生不知道小数点后面究竟是包括“0”在内的几位数。悉心分析，原来是学生的算理不清，缺乏整体把握与结构性理解。因此，我们组织学生通过学科大概念的理解，认真观察竖式特征，进行多元表征，从中体会算理本质。

大屏幕呈现用竖式计算的商的过程，学生观察之后，教师设问：余数由“1”变为了“10”，其意义是什么？商为“2”，意义又是什么呢？请看以下思考过程（如图1）：

这样的表征实际上是不断细分的过程，是把1看成了10个0.1的细分过程。以此类推，10个0.1除以5的结果是2个0.1。明白了这一点，哪里点上小数点以及把“2”写在哪里，答案呼之欲出。

（三）迁移推理，感受运算本质

小数除法意味着计数单位更小。教师的责任就在于引领学生在不断细分的过程中迁移推理，左右贯通，发现运算本质，发现知识之间的“起承转合”，达到“一通百通”的目的。而这，正是成功把握学科大概念之后学习的理想境界。

针对9÷4的竖式出现的“10”与“20”，必要的迁移推理不可或缺：如果0.1不够分，可以继续细分，只需要在小数点后面添加“0”即可，0.01，0.001……这与整除除法的规律是一致的。

可见，“数的意义”与“数的运算”之间有关联，数的表示与运算方法有关联，整数除法与小数除法在算理上有关联……教师的责任就在于引领学生自己发现这样的关联，自己学会迁移推理，自己依托学科大概念成功解决问题。

（四）对比梳理，凸显算理一致

在不断的迁移推理中，学生不难发现：“被除数和除数同时除以相同的数（0除外）后商不变”，这个性质是可以通用到所有数的运算中。说做就做，相当一部分学生在重温转化思想之后，勇敢地进行新旧知识的算理贯通。以下是两次对比梳理。

1.第一次对比。教师分小组让学生计算并观察3.2÷0.5和32÷5的商，总结两者之间的共性，发現依托学科大概念进行计算的意义。

2.第二次对比。利用展板在大屏幕上展示学生完成的几组算式（包括错题），组织学生观察、讨论后进行汇报，发现运算规律，总结经验教训（如图2）。

这样的对比梳理是有意义的：由9÷0.4到90÷4，学生由此及彼，通过熟稔运用转化思想，变孤立为融通，形成上挂下联的局面。这种局面让学生学得轻松而高效，达到了减负增效的目的。

基于学科大概念，在变中找不变，在整体勾连中“多走了几个来回”，“促使学生形成科学严谨的思维习惯，培养推理意识。”[3]这种“习惯与意识”能够让学生受用终生，能够为“双减”政策在小学数学学习中的有效落地提供持久的动能。数学教师应该基于学科大概念进行系统化建构，为减负增效提供支撑。

参考文献：

[1] 王玉彬，姚颖.探索运算本质构建运算联系[J].小学数学教育，2022（5）.

[2] 侯燕妍.以理驱法，体会运算一致性[J].教学月刊小学版（数学），2023（1-2）.

[3] 冯玉新.注重“一致”整体施教贯通“理法”促进学习[J].福建教育，2023（1）.

课题项目：甘肃省教育科学“十四五”规划2023年度重点课题“‘双减背景下依托‘学科大概念开发课堂教学优质资源及应用研究”（GS[2023]GHBZ133）

编辑/赵卓然