改进的区间值对偶犹豫模糊集距离测度及其应用

袁伟斌, 王惠文

(云南师范大学 数学学院, 云南 昆明 650500)

0 引言

由于人们主观偏好日益复杂和模糊,模糊性已成为决策过程的一部分,因而模糊决策理论已发展成一个研究热点.1965年Zadeh[1]首次引入模糊集的概念,不同拓展形式的模糊集应运而生.1986年Atanassov[2]加入了非隶属度,定义了直觉模糊集;2010年Torra[3]引入了犹豫模糊集的概念,它允许隶属度有多个值,更能反映出决策者的犹豫态度.2012年Zhu等[4]提出了对偶犹豫模糊集理论,增加了非隶属度,以及允许都可以有多个可能值.2014年Farhadinia[5]提出了区间值对偶犹豫模糊集的概念,它其中的隶属度与非隶属度都是以区间形式出现,更具一般性.

在实际决策问题中,距离测度是一重要指标,从而应用广泛.例如聚类分析[6]、图像处理[7]、投资选择[8-9]、医学诊断[10]、模式识别[11]、分配问题[12]等.Wang等[13]研究了对偶犹豫模糊集的距离测度及相似测度;王金英等[14]、李丽颖等[15]提出了区间值对偶犹豫标准海明距离公式,但这些距离测度都需要主观填充数据,可能会导致信息失真的情况.因此,本文提出了区间值对偶犹豫模糊距离测度的公理化定义,并给出基于区间对偶犹豫度、隶属度与非隶属度完全偏差的距离公式.最后通过一个多属性决策实例说明其合理性.

1 预备知识

定义1[14]设X为一固定集合.称

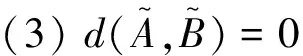
基于上述距离的定义,文献[14]提出区间值对偶犹豫标准Hamming距离.

(1)

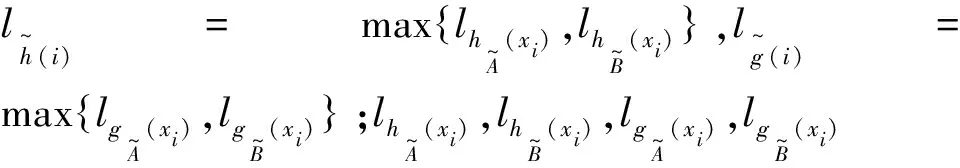
从公式(1)可知,计算时需要人为填充元素,从而使得两个集合元素个数相同.填充原则有乐观原则,悲观原则等,但这样的做法没有保证数据的真实性,可能会导致信息失真,因此有必要重新考虑区间值对偶犹豫模糊集的距离测度.

2 改进的区间值对偶犹豫模糊集距离测度

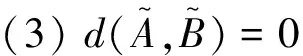
中的元素个数.

定义5设

的区间对偶犹豫度定义为:

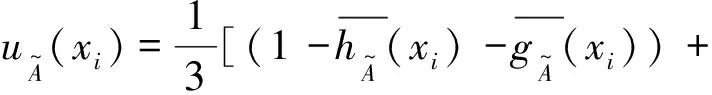
其中

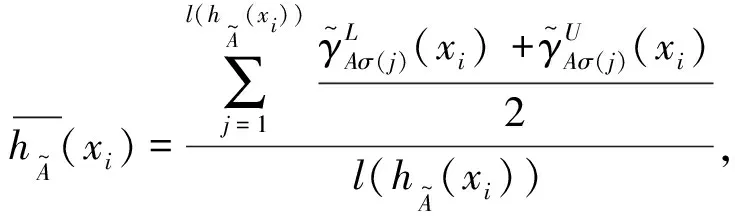
其中λ∈[1,+∞).

结合上述三个偏差距离,给出改进的区间值对偶犹豫模糊集距离测度如下.

(2)

其中参数ρ,θ,ξ∈[0,1],ρ+θ+ξ=1.

由于不同属性之间也有一定差异,因此有必要将不同属性的权重考虑在距离测度中.

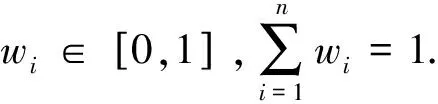
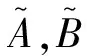
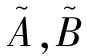
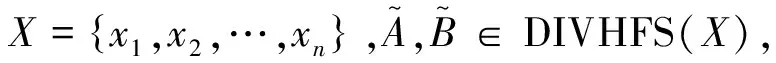
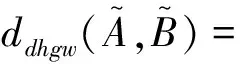
(3)

其中参数ρ,θ,ξ∈[0,1],ρ+θ+ξ=1.

引理1(Minkowski不等式)任给(a1,a2,…,an),(b1,b2,…,bn)∈Rn,λ≈1,则有:

证明设

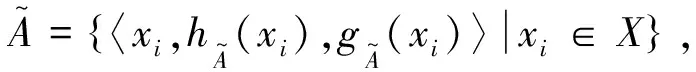
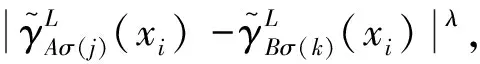
故有

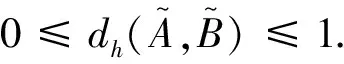
可得

同理可得

从而有

必要性:反之显然成立.故性质(3)满足.

4)结合引理1,可知:

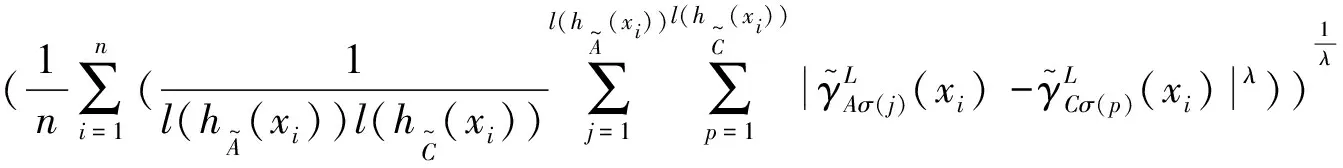
于是可得

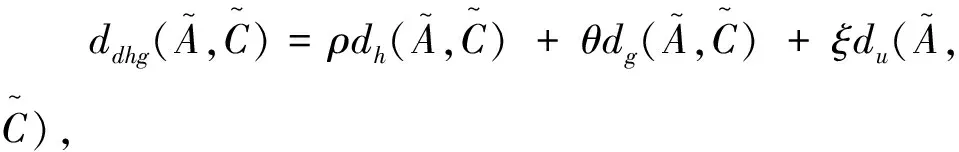
因此性质(4)满足.

3 数值算例

考虑文献[14]中的例子,设有5个投资方案Ai(i=1,2,3,4,5),每个方案有4个评价属性Cj(j=1,2,3,4),属性的权重为w=(0.2,0.35,0.3,0.15),专家给出的评价矩阵如表1所示.

表1 区间值对偶犹豫模糊评价值

假设理想方案为A*=({[1.0,1.0]},{[0.0,0.0]}),下面按照上文给出的改进的区间值对偶犹豫广义加权距离公式,计算出每个备选方案与理想方案之间的距离,距离测度值越小,则方案越优.

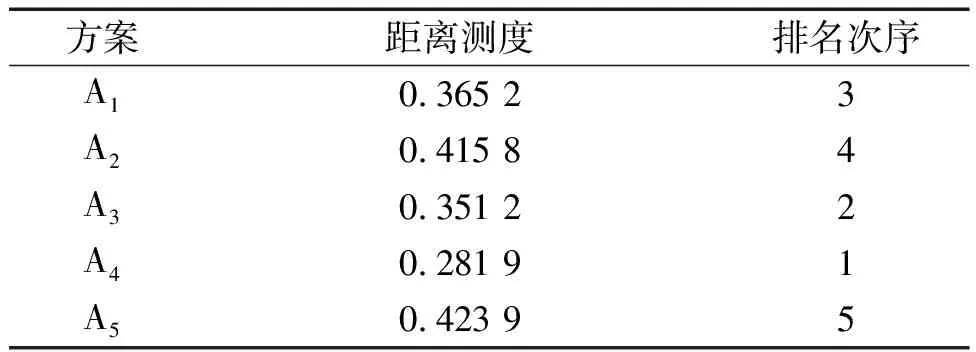
表2 等权重下的距离测度值及排名结果

由表2可知,方案排序为A4>A3>A1>A2>A5,最优方案为A4,这与文献[14]中的排序A4>A1>A3>A2>A5略有差异,由于使用的距离测度公式不同,从而导致最终的方案排名结果也不同,但最优方案都是A4,从而也说明改进的距离测度的合理性.

改进的距离公式中参数ρ,θ,ξ分别表示决策者对隶属度信息,非隶属度信息,犹豫度信息的偏好程度.表3通过对ρ,θ,ξ的不同取值,来体现决策者的不同偏好态度.

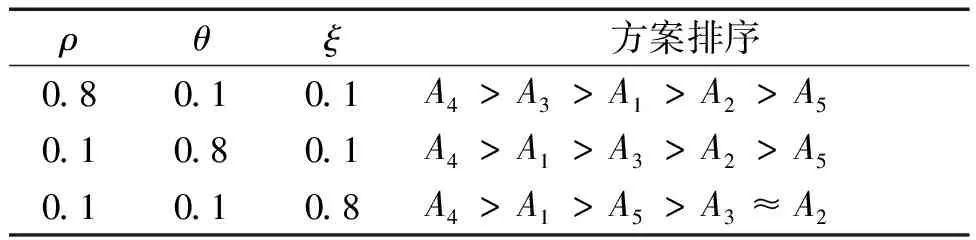
表3 不同偏好下的方案排序结果

从上表可知,当决策者对不同信息的偏好程度不同时,方案排序也会随之变化,但最佳方案始终未变.因此,改进的距离公式可以根据决策者的不同偏好程度,选择不同的偏好参数值,从而提供了更多的选择.

4 小结

本文提出了区间值对偶犹豫模糊集距离测度的公理化定义,给出了改进的距离公式,并给予了证明.改进的距离公式加入了偏好参数,能体现出不同决策者的偏好态度.最后结合一个实际的模糊多属性决策案例, 通过结果比较,偏好参数分析,说明了改进的距离测度的有效及合理性.接下来可以在此基础上做其他深入的研究,例如利用改进的距离测度进行聚类分析,构造区间值直觉对偶犹豫模糊集的相似性测度等.