一类带有疫苗接种传染病模型的全局稳定性和分岔分析

杨洛驿, 刘玲伶

(西南石油大学 理学院, 四川 成都 610500)

0 引言

Covid-19是一种新型冠状病毒感染,在病毒大流行期间,各国都采取了一些系列的有效措施来切断其传播,如戴口罩、病毒传播链溯源、修建方舱医院等外部管控措施,但从长远来看最有效的应该是人类自身免疫系统去战胜病毒,其中通过疫苗接种能够使人群对病毒产生免疫力和抵抗力,减少感染率和死亡率,起到间接保护效果,从而降低疫情防控造成的经济资源成本.疫苗接种不仅可以保护接种者自身,还可以减少传染源和传播途径,同时当社会中的大部分人群在接种有效的疫苗后,基本可以实现疫情的清零,因此疫苗接种为疫情防控提供更加全面的保障[1].许多学者希望通过数学建模来探讨生物模型的动态发展[2-3],研究病毒传播模式可以模拟当前流行病的发展,并为制定疫情管理措施提供指导[4].目前科学界对其流行病学、特征、临床表现等方面有了更深入的研究,由于新型冠状病毒感染的潜伏期不同,早期使用感染-再感染(SIR)模型及其扩展的研究可能不准确,而暴露-感染-再覆盖(SEIR)模型及其延伸更为合适[5].

SEIR模型是一种广泛应用于现代流行病学的数学模型,该模型将人群分为四个相互转化的种群:易感者、暴露者、感染者和康复者,通过对人群状态的转化进行建模分析此类模型,可以有效预测疾病在人群中的发展趋势[6].由于疫苗接种对于传染性疾病具有重要意义,针对之前的SEIR模型没有考虑疫苗接种对于病毒传播的影响,2020年Nazarimehr等[7]提出了一类带有疫苗接种的新型冠状病毒感染SEIR模型,改进模型如下:

(1)

其中μ是各类人群的死亡率,β是病毒从易感人群转换到暴露人群的速率,v是疫苗接种的恢复率,σ是由暴露人群转移到感染人群的速率,γ从感染人群转移到恢复人群的速率.这一类模型可以用来分析新型冠状病毒感染在人群中的传播和疫苗接种对疫情的影响,通过这个模型可以知道一部分易感人群可以直接通过疫苗接种转化成为康复者,以此缩小疫情的进一步发展[8].此类模型除了可以用作新型冠状病毒感染的研究外,还可以应用于其他疾病的控制和管理,如流感、麻疹、水痘等,这些疾病也是全球公共卫生的重要问题,疫苗接种是控制和预防这些疾病的重要手段,因此,带有疫苗接种的SEIR模型具有广泛的应用前景和实际意义.

本文讨论了此类带有疫苗接种的新型冠状病毒感染SEIR模型,首先给出了系统平衡点存在的参数条件,通过计算基本再生数给出了边界平衡点和内部平衡点的局部稳定性,并进一步构造Lyapunov函数和变分矩阵的方法给出了系统的全局稳定性.当基本再生数跨过1时,讨论了系统边界平衡点附近将发生跨临界分岔的情形,最后结合数值模拟展示系统稳定性的情况,从生物学上给出模型动力学行为的分析.

1 平衡点存在性和局部稳定性分析

下面讨论系统(3)平衡点的存在性和稳定性.

考虑生物意义可知各参数均大于0,其中系统(1)人数N(t)=S(t)+E(t)+I(t)+R(t),且dN/dt≡0,可知总人数为定值,可将系统(1)进行简化:令变换

X=S/N,Y=E/N,Z=I/N,H=R/N,

则将系统(1)转化为:

(2)

由系统(1)的人群关系可得

X(t)+Y(t)+Z(t)+H(t)=1,

H(t)=1-X(t)-Y(t)-Z(t).

利用人口总数是常数的假设,则可将上述系统(2)转化为如下三维系统:

(3)

该模型的可行域为:

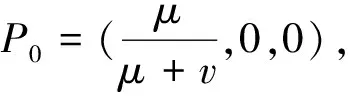
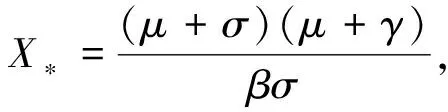
证系统平衡点满足如下条件:

(4)

通过求解上述方程可得:

其中

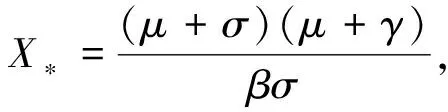
下面计算系统(3)的基本再生数.

在边界平衡点P0处,Fi(x),Vi(x)的雅可比矩阵为:

通过计算再生矩阵R0=ρ(FV-1),得到基本再生数:

(5)

下面对系统(3)进行平衡点稳定性分析.

定理1当R0<1时,边界平衡点P0是渐近稳定的,当R0>1时,边界平衡点P0是不稳定的,内部平衡点P*是渐近稳定的.

证边界平衡点P0的雅可比矩阵如下:

系统(3)在边界平衡点P0处的特征多项式为(λ+μ+v)(λ2+aλ+b),此时存在一个特征根为λ1=-μ-v,分析后面关于λ的一元二次方程,化简可得:

通过对应系数相等可得:

a=(2μ+γ+σ),

(1-R0)(μ+σ)(μ+γ).

由一元二次方程的韦达定理可知,λ2λ3=b,λ2+λ3=-a,特征多项式的两个特征根λ2,λ3的具体情况如下:(1)当R0<1时,特征根λ2<0,λ3<0,边界平衡点P0是渐近稳定的;(2)当R0=1时,特征根λ2=0,λ3<0,边界平衡点P0是非双曲平衡点;(3)当R0>1时,特征根λ2>0,λ3<0,边界平衡点P0是不稳定的,定理证毕.

下面证明内部平衡点P*的稳定性.

系统(3)在内部平衡点P*处的雅可比矩阵为:

对应的特征多项式:F(λ)=a0λ3+a1λ2+a2λ+a3,对应系数如下:

a0=1,a1=γ+3μ+σ+v+(μ+v)(R0-1),a2=(μ+v)(γ+2μ+σ)R0,a3=(μ+v)(μ+γ)(μ+σ)(R0-1).

当R0>1时,满足ai>0,计算可得a1a2-a3>0.因此当R0>1时,有主子式

Δ3:=a3·Δ2>0,

根据Routh-Hurwitz定理可得,内部平衡点P*是渐近稳定的,因此定理1得证.

2 全局稳定性

下面进行系统(3)的全局渐近稳定性分析.

定理2当R0<1时,边界平衡点P0是全局渐近稳定的;当R0>1时,内部平衡点P*是全局渐近稳定的.

证在可行域T内,构造Lyapunov函数

V=σ·Y+(μ+σ)·Z≥0,

当R0<1时,

dV/dt=σ·(βXZ-(μ+σ)Y)+(μ+σ)·

(σY-(μ+γ)Z)=

Z·(μ+σ)(μ+v)(R0-1)<0,

其中,当Z=0时,dV/dt=0,由Lasalle不变集原理可得,边界平衡点P0是全局渐近稳定的.

下面证明内部平衡点P*的全局稳定性.

利用文献[10]中变分矩阵的方法证明内部平衡点P*全局渐近稳定性,系统(3)内部平衡点P*处的雅可比矩阵如下:

则对应的第二变分矩阵如下:

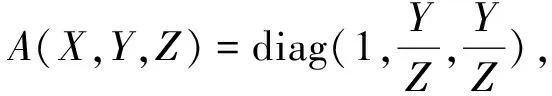
其中

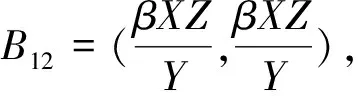
R3上的范数

|(μ,v,w)|=max{|μ|,|v|+|w|},

其中

η(B)≤max{g1,g2},

g1=η1(B11)+|B12|,g2=η1(B22)+|B21|,

η1是相对于L1矩阵范数的测度,而|B12|,|B21|是L1的矩阵范式.通过计算可得:

因此

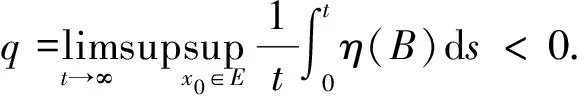
3 跨临界分岔

下面将对系统(3)在R0=1处的分岔情况进行分析.

定理3在R0=1处,系统(3)在边界平衡点P0附近将会发生跨临界分岔.

证将平衡点在P0处移到原点,进行坐标平移,令

系统(3)转化为如下等价系统:

(6)

令分岔参数ξ=βμσ-(σ+μ)(γ+μ)(v+μ),可得

当R0=1时,ξ=0,雅可比矩阵如下:

特征多项式有特征根

λ1=-μ-v,λ2=0,λ3=-2μ-γ-σ.

对于特征根λ2=0,有对应特征向量

上述雅可比矩阵的转置如下:

对于上述转置后矩阵有特征根λ=0,对应的特征向量φ=(φ1,φ2,φ3)T=(0,σ,μ+σ)T.

令f=(f1,f2,f3),则原方程可得:

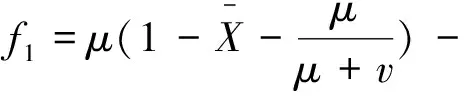
通过计算得到:

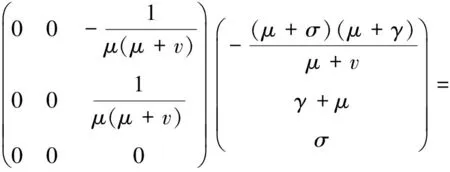
因此

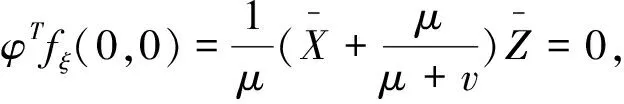
所以由Sotomayor定理[12]知,在ξ=0(R0=1)处,系统(3)将在P0附近发生跨临界分岔,定理3得证.

定理(5)分析的分岔现象表明,平衡点的稳定性随着参数取值的变化而发生突变,从而导致病毒传播速度不断增加,需要采取有效措施来控制疫情的蔓延,如限制人口流动、加强卫生防护、推广有效疫苗接种等.同时应密切关注病毒传播的发展趋势,阻止或延缓分岔现象的出现,避免造成更大的经济与人力资源损失.

4 数值模拟和生物意义

本节利用Matlab软件中“ode45”对系统(3)进行数值模拟.

选取参数μ=0.012,β=0.090,v=0.100,σ=0.038,γ=0.090,由基本再生数(5)计算可得R0<1,由引理1可得系统(3)此时仅存在一个边界平衡点,且由定理2知边界平衡点是全局渐近稳定的.图1(d)显示,随着时间变化,轨线最终趋于边界平衡点.分析各类人群可得,易感人群(S)随着时间先下降并趋于稳定(见图1(a));由图1(b)、(c)可知暴露人群(E)和感染人群(I)随时间不断降低,疫情得到了有效控制.但需要注意的是,即使感染人群已经降低至零,仍然存在一部分易感人群,因此需要加强疫情监测和防控工作,及时发布疫情信息,提高公众疫情防控意识,及时采取必要的隔离和治疗措施,同时应加强社会宣传和防疫教育,提高公众对病毒传播途径、防护措施等方面的了解,注意个人防护和纠正不良卫生习惯,增强身体免疫力,更好地保护自己和他人.

选取参数μ=0.012,β=0.560,v=0.010,σ=0.050,γ=0.003,由基本再生数(5)可得R0>1,由引理1可知此时存在一个内部平衡点.且由定理2可知内部平衡点是全局渐近稳定的.图2(d)可以看出,随时间变化,轨线趋于内部平衡点;观察各类人群,由图2(a)可知,易感人群(S)随时间不断减少并逐步增加至定值;图2(b)显示,暴露人群(E)随时间先增加再减少至定值;图2(c)可知感染人群(I)随时间迅速增长并缓慢减少到达饱和状态.通过分析可知,在疫情传播初期病毒的传播速度非常迅速,容易导致疫情快速扩大.因此,需要尽快采取措施切断病毒的传播途径,比如加强个人防护、避免密闭空间的聚集、加强社交距离的管理等措施.此外,针对感染者和密切接触者,应及时进行隔离和检测管理措施,同时可以看到随着时间的推移,感染者数量逐渐达到一个饱和峰值,这个阶段应当积极协调资源,做好感染后的治疗措施,加强完善医疗卫生系统的建设,避免造成二次感染.

(a)易感人群

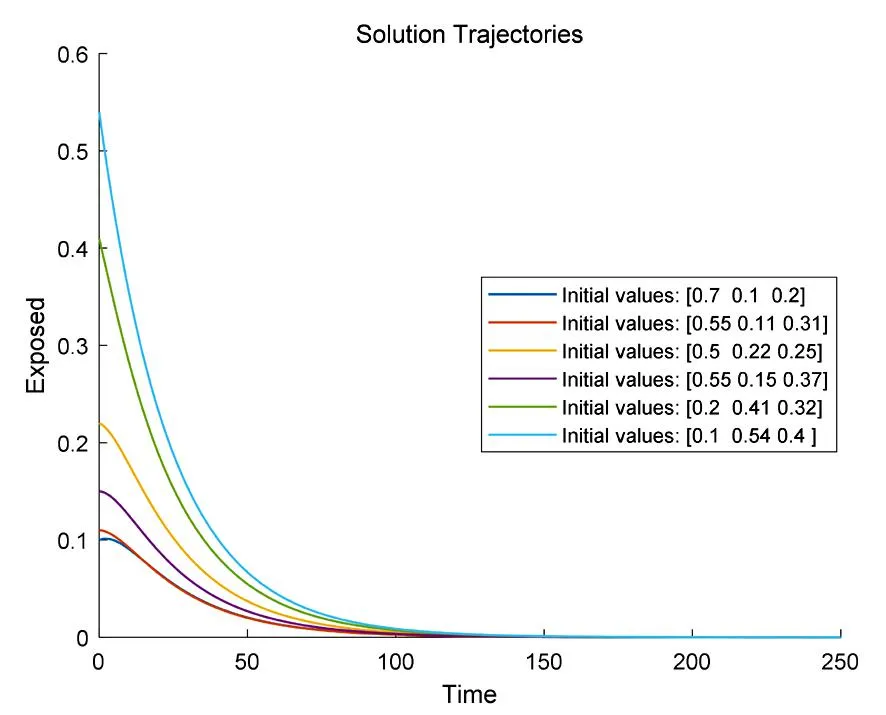
(b)暴露人群

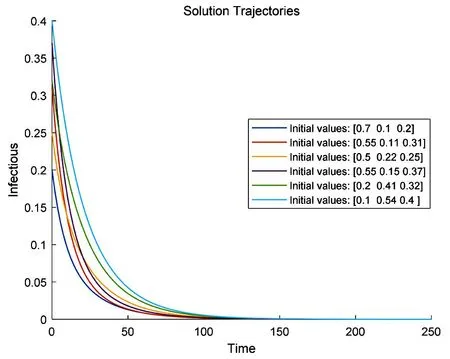
(c)感染人群

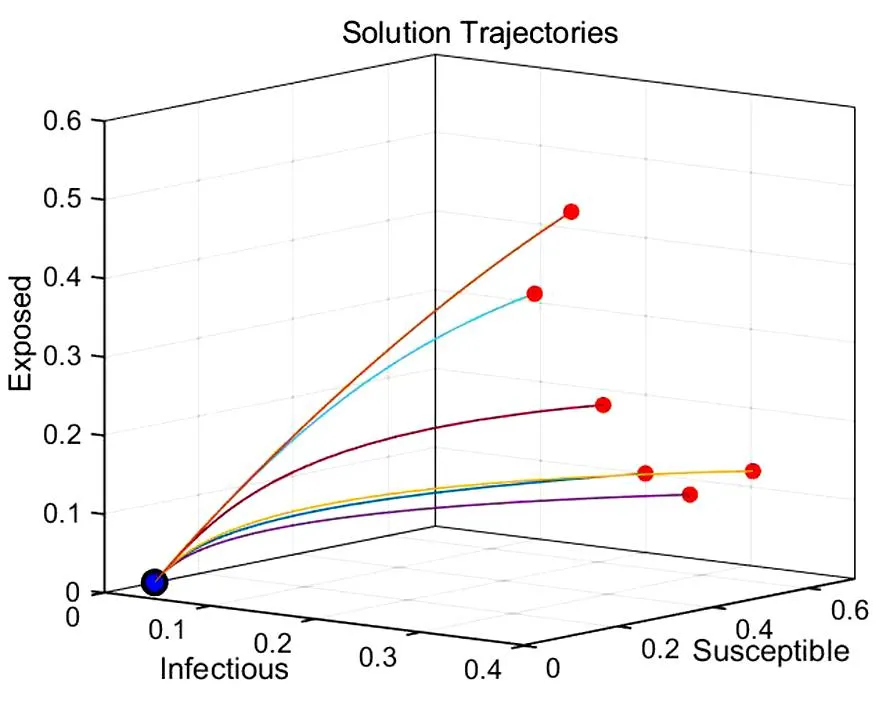
(d)解

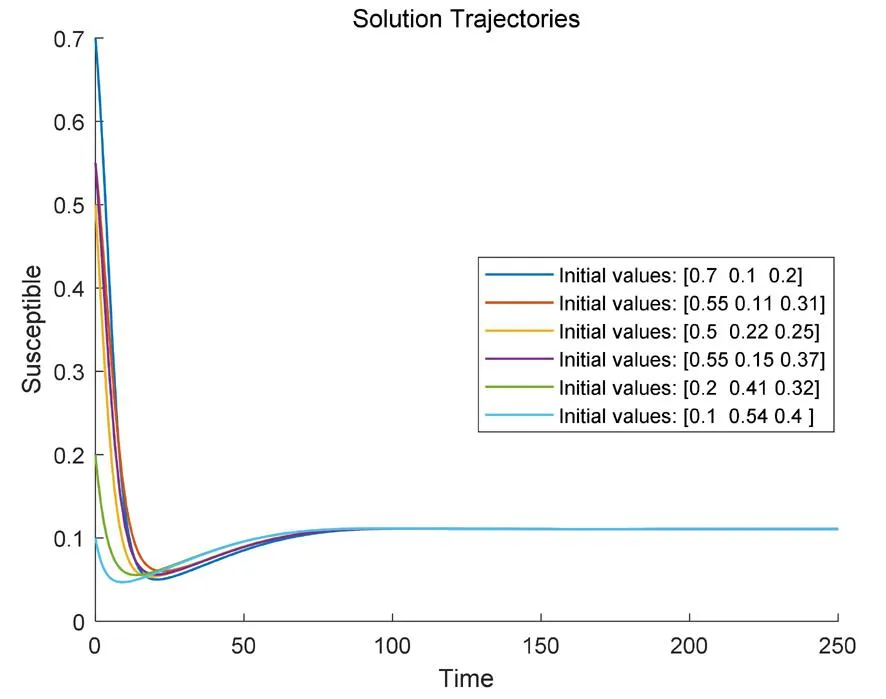
(a)易感人群的轨迹图

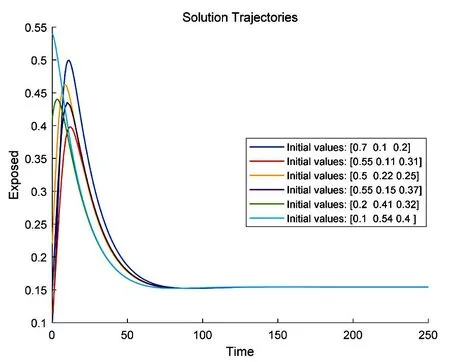
(b)暴露人群

(c)感染人群

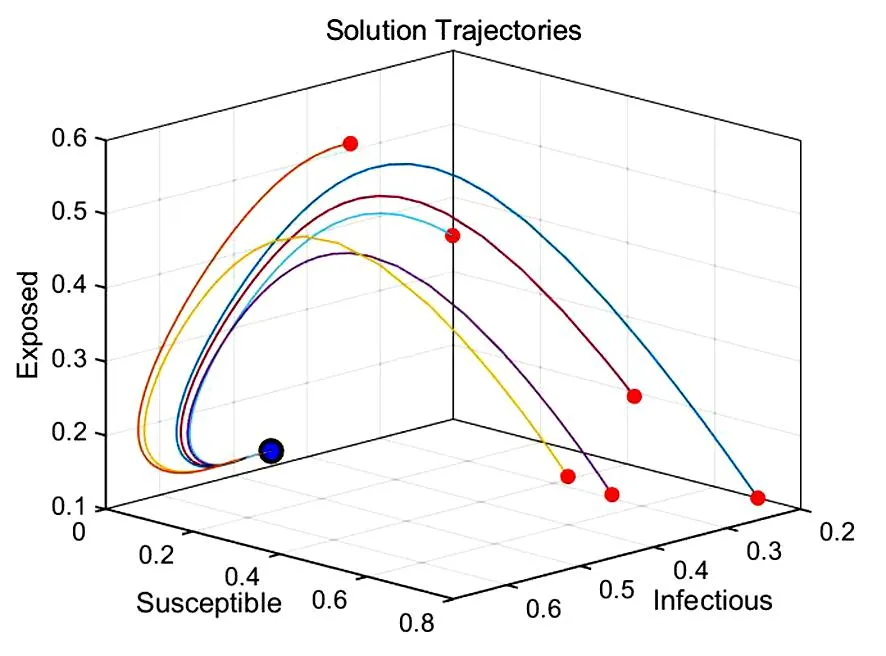
(d)解