三参数burr分布的几何结构

罗 洁, 万文龙, 许 皓

(西华师范大学 数学与信息学院, 四川 南充 637009)

0 引言

Amari[1]提出的信息几何从现代微分几何的角度研究统计流形.近年来,由于概率论、信息论和统计学中的一些非常重要的结构可以使用微分几何来处理,因此它在许多相关的学习领域中得到了广泛的研究和应用.与此同时Amari[2]还提出了离散概率分布统计模型的不同几何方法,这极大地促进了信息几何的发展.根据信息几何的理论,研究者们建立了不同的统计流形[3-8],研究了其相关的几何性质,像Beta流形的α-几何结构[3],常φ-曲率Sasaki统计流形[4]等统计流形.另外,信息几何还讨论了统计流形的性质[9-11],它对神经网络、信号处理、机器学习等不同领域有着极为重要的作用.

Burr分布[12-13]是Burr XII型分布,是Burr系统中十二种连续分布之一,它在保险精算学[14]、环境科学[15]以及社会经济学[16]等领域都有广泛的应用.例如,在空中交流时,机头时距[17]的变化符合三参数burr分布特征.Shao[18]研究了三参数Burr分布的分布函数的渐近性质,随着参数趋于边界,分布趋于非退化的极限形式.许多学者对毛刺分布有着浓厚的兴趣,并对其进行了相应的研究.

本文的内容组织如下:第1节给出了后面章节中使用的关于信息几何的数学背景的许多关键结果,第2节介绍了三参数burr分布流形的几何结构,第3节给出了三参数burr分布流形的两个子流形及其相关几何结构,第4节为总结展望部分.

1 统计流形

定义1统计流形[1]假设M={p(x)=p(x;θ)|θ=(θ1,θ2,…,θn)}是一个由n维参数向量θ=(θ1,θ2,…,θn)参数化的正则统计模型,其中p(x)是概率密度函数.这样,我们将概率密度函数族的集合M称为n维统计流形.

定义2子流形[1]设M和N是两个光滑流形,若有光滑映射φ:M→N,使得

(1)φ是单一的;

(2)在任意一点p∈M,且映射φ都是非退化的;

则称(φ,M) 是N的一个光滑子流形,或称嵌入子流形.

定义3Fisher信息矩阵[2]在信息几何中,黎曼度量由Fisher信息矩阵表示.对于密度函数p(x),Fisher信息矩的分量可定义为

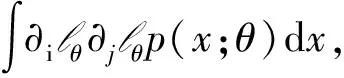
(1)

其中,lθ=l(x;θ)=lnp(x;θ)为对数似然函数,以及∂i=∂/∂θi,然后,称M={p(x;θ)}是n维统计流形,g=[gij]是M的Fisher信息矩阵,[gij]=[(gij)-1]是[gij]的逆矩阵.

定义4克里斯托符号[10]统计流形M的克里斯托符号的定义为

(2)

其中[gij]=[(gij)-1]是[gij]的逆矩阵.

定义5α-联络[11]在n维统计流形M中,[gij]是Fisher信息矩阵,统计流形M上的α-联络系数为

(3)

其中三阶张量为

Tijk=Eθ[∂il(x;θ)∂jl(x;θ)∂kl(x;θ)].

定义6黎曼曲率[11]统计流形M的黎曼曲率张量定义为

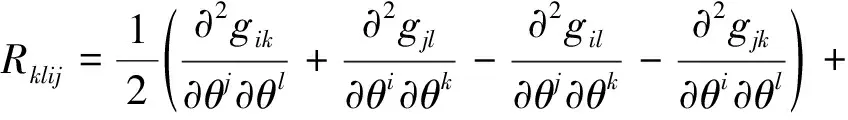
(4)

2 三参数burr分布流形的几何结构

三参数burr分布的概率密度函数为

其中,θ=(α,τ,λ),α>0是形状参数,λ>0是尺度参数,以及τ>0.根据统计流形定义三参数burr分布流形,即

定理1具有自然坐标系θ=(α,τ,λ)的三参数burr分布流形的Fisher信息矩阵为

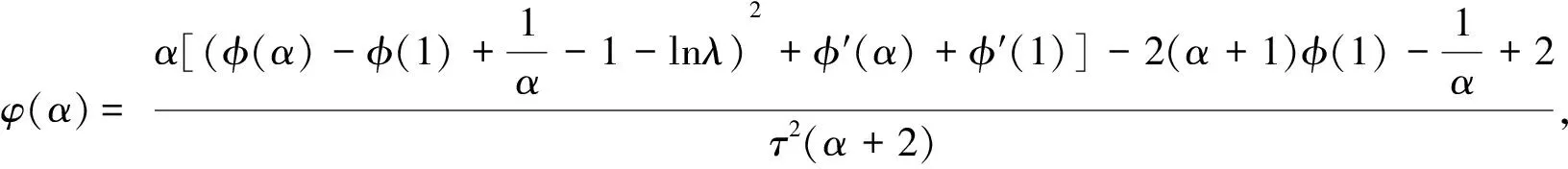
证明由(1)可知,三参数burr分布函数的对数似然函数为

l(x;θ)=lnp(x;θ)=ln(α)+ln(τ)-ln(λ)+

对对数似然函数进行一阶求导,得

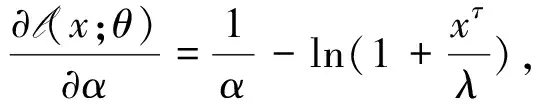
再求对数似然函数的二阶偏导数,得

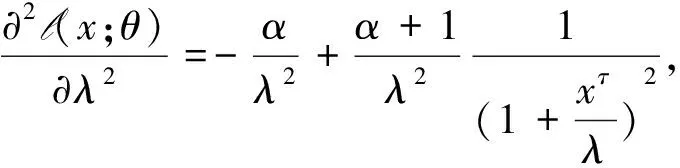
根据二阶偏导数求Fisher信息矩阵分量

定理2三参数burr分布流形的信息矩阵[gij]的逆矩阵[gij]分量分别为

其中,

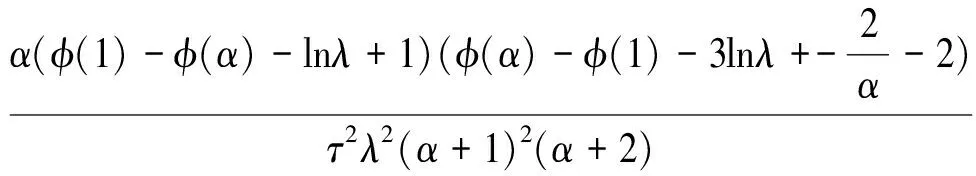
定理3根据公式(3)可得三参数burr分布的α-联络系数分别为

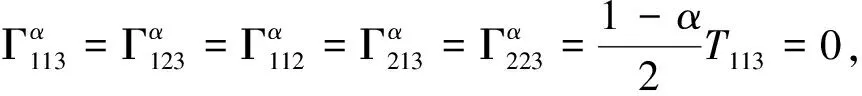
定理4根据公式(3)可以得到三参数burr分布流形的黎曼曲率

3 三参数burr分布的子流形

3.1 两参数burr分布流形的几何结构

当λ=1时,我们得到两参数burr分布函数,它的概率密度函数为

其中α>0,τ>0.从而根据前面统计流形的定义,可得两参数burr分布流形为

定理5两参数burr分布流形的Fisher信息矩阵为

其对应的行列式为

证明两参数burr分布函数的对数似然函数为

l(x;θ)=lnp1(x;θ)=

lnα+lnτ+(τ-1)lnx-(α+1)ln(1+xτ),

对对数似然函数求导,得

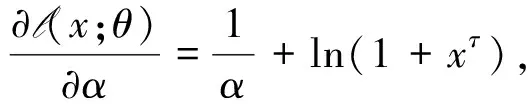
然后,计算Fisher信息矩阵的分量分别为

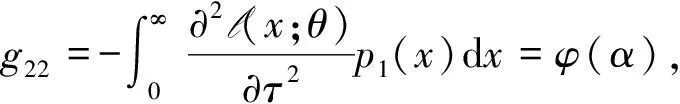
由此,可以计算两参数burr分布的Fisher信息矩阵的行列式值为

定理6两参数burr分布流形中,Fisher信息矩阵[gij]所对应的逆矩阵[gij]的分量分别为

定理7根据公式(2),可以计算出两参数burr分布流形的克里斯托符号分别为

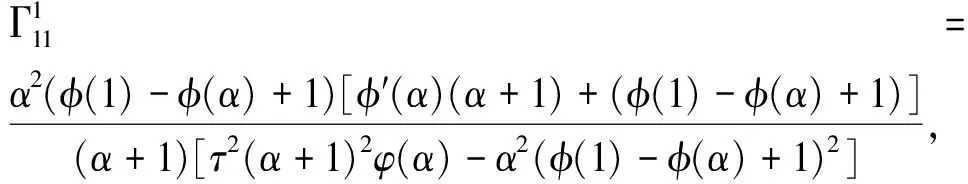
定理8根据公式(3),两参数burr分布流形的α-联络分别为

3.2 Pareto分布流形的几何结构

当τ=1时,得到Pareto分布的密度函数为

p2(x;θ)=αλα(λ+x)-(α+1).

由此定义Pareto分布流形

M2={p2(x;θ)|p2(x;θ)=αλα(λ+x)-(α+1)},

其中α>0,λ>0.

定理9Pareto分布流形的Fisher的信息矩阵为

证明Pareto分布的对数似然函数为

l(x;θ)=lnp2(x;θ)=lnα+αlnλ-(α+1)ln(x+λ).

对对数似然函数进行求导可得

从而,计算Fisher信息矩阵分量如下

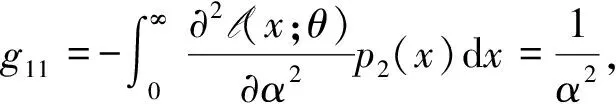
由此可计算出Pareto分布的信息矩阵对应的行列式为

它的行列式值图像如图1所示,随着α和λ的增大,行列式值断崖式下降,整个图像呈现瀑布型.

图1 Pareto分布流形的行列式值图像

定理10Pareto分布流形的信息矩阵[gij]所对应的逆矩阵[gij]分量分别为

g11=α2(α+1)2,g12=λα(α+1)(α+2),

定理11根据公式(2),可以计算出Pareto分布流形的克里斯托符号为

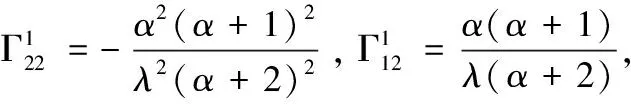
定理12通过公式(3),可以计算Pareto分布流形的α-联络分别为

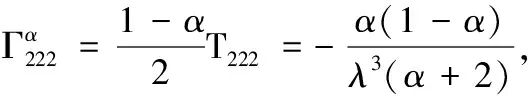
定理13根据公式(4),Pareto分布流形的黎曼曲率为

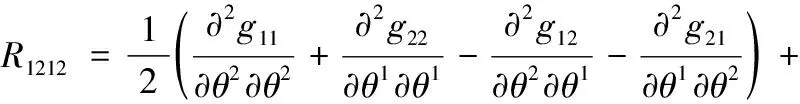
Pareto分布流形的黎曼曲率图像如图2所示,随着α和λ的增大,黎曼曲率值不断下降,不断接近于零.

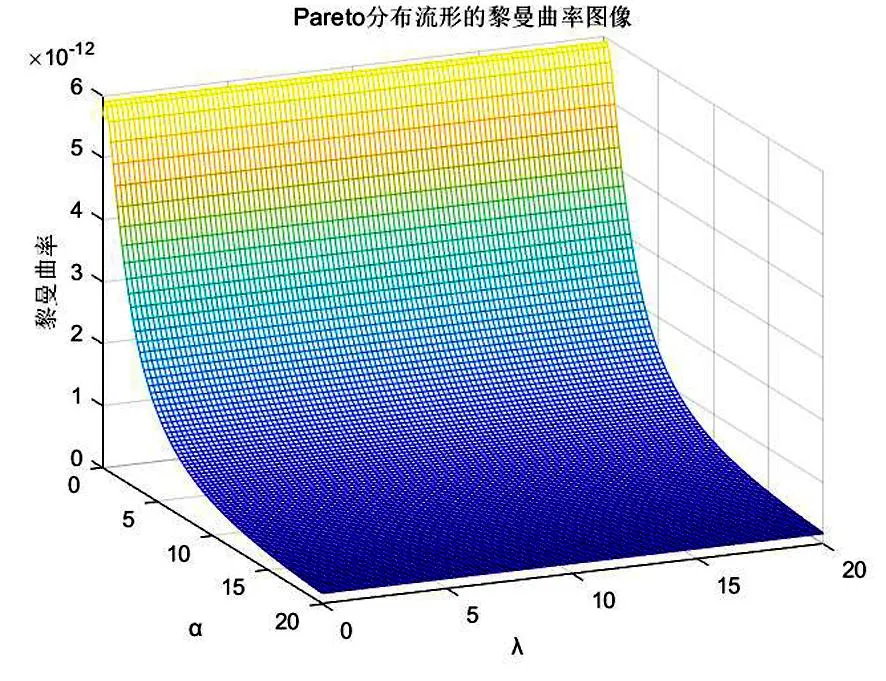
图2 Pareto分布流形的黎曼曲率图像

4 总结

本文通过信息几何的理论建立了三参数burr分布流形及其子流形,根据计算得到了三参数burr分布流形及其子流形的几何结构,其中主要计算了其Fisher信息矩阵及其逆矩阵、行列式值、α-联络系数以及黎曼曲率等几何量.这对于三参数burr分布的几何结构会有更加深刻的理解,在后续的保险精算、概率研究、公路与水力运输等领域也有广泛的应用.另外,在解决更加复杂的问题时,或许从信息几何的角度来看,三参数burr分布的几何结构有更大的研究价值,如何将这些结果运用到与三参数burr分布相关的实际问题中,并且得到有效的解决方法是未来将要进行的研究.