稳态性能下T型槽柱面气膜密封结构参数非线性回归分析*
熊忠汾 刘美红 韦邱发 李 鑫
(昆明理工大学机电工程学院 云南昆明 650504)
气膜密封技术能够利用气体介质的动压效应,在密封界面间形成微米级的气膜,从而使得密封界面保持非接触的密封方式。气膜密封能够在降低泄漏量的同时,减少动、浮环密封界面磨损,提高密封系统在高速透平机械中的可靠性与长周期寿命,因而在高速流体机械中,气膜密封是一种非常有效的密封方式,并成为密封研究中的热点[1-3]。
在气膜密封中,端面密封技术被研究人员广泛研究并得以应用。但在航空发动机转子系统中,由于工作环境影响而产生的位移形变以及转子存在着较大的径向跳动[4],使得端面密封技术受到限制。而柱面气膜密封由于具有较大的柔性,能够适应转子的径向位移[5-7],成为一种重要的密封形式。T型槽柱面气膜密封因其结构特性,能够适应转子双向旋转,并且有着优异的密封性能,成为研究人员的重点研究对象之一。
胡文绩、李涛子等[8-9]使用Fluent进行仿真试验,研究了T型槽干气密封的稳态性能,同时也验证了使用数值模拟方法的可行性。王衍等人[10]针对改良T型槽槽型结构参数,使用数值模拟的方法研究了开启力的变化规律。彭旭东、苏泽辉等[11-13]在不同工况条件下分析了T型槽稳态性能的变化情况,发现槽长坝长比等结构参数对气膜刚度和泄漏率有着较大的影响。然而,目前关于各因素对T型槽稳态性能影响程度的分析判断的文献还很少见。因此,本文作者研究了结构参数的变化及其关联特征对T型槽柱面气膜密封稳态性能的影响,比较了各结构参数的影响程度,为实际工程应用提供参考。
1 数值计算模型
1.1 T型槽柱面气膜密封系统工作参数
表1给出了密封气膜系统完整的结构参数。根据表1给出的结构参数,使用Creo三维辅助设计软件完成对柱面气膜密封系统的建模。T型槽柱面气膜密封结构简图如图1(a)所示,图1(b)示出了单个槽型的平面几何尺寸。其中l为气膜轴向长度,w1和wq分别是T型槽窄槽宽度和宽槽宽度,wr为非槽区平台宽度,βr和βg分别是宽槽长度和窄槽长度。
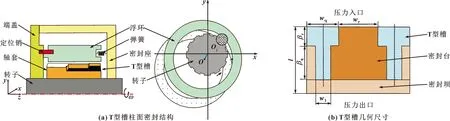
图1 T型槽柱面密封结构及几何尺寸
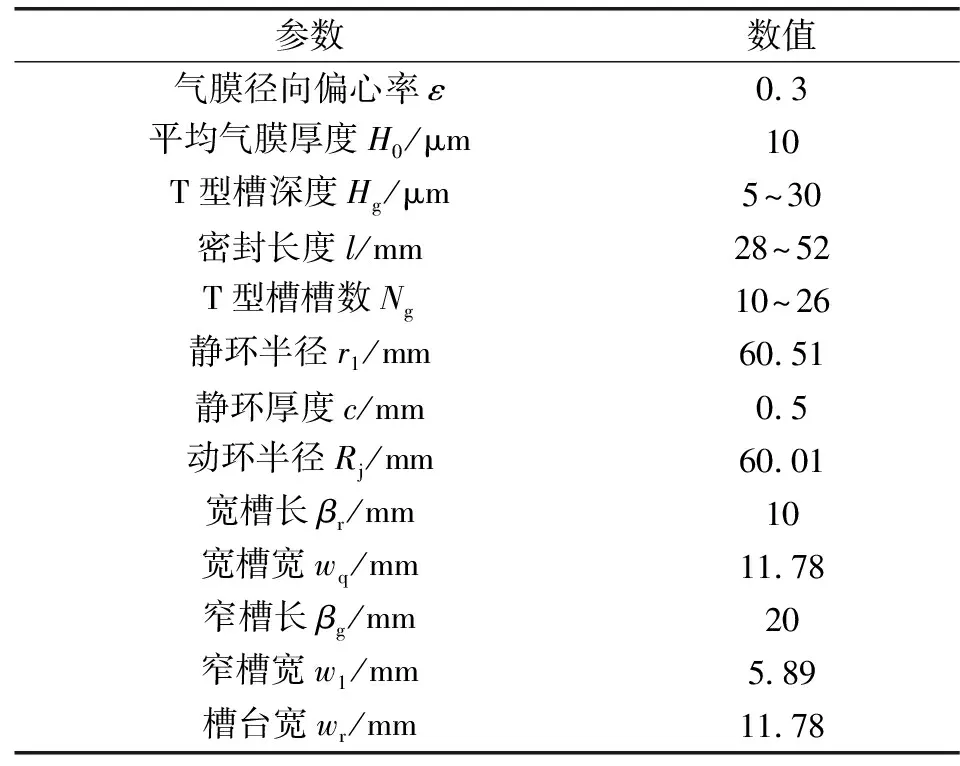
表1 T型槽柱面气膜密封系统结构参数
1.2 材料属性
参考文献[14]的研究成果,选择密封环的材料和对应属性如表2所示。

表2 动静环材料属性
进行数值模拟求解时设置密封流体为空气,其密度为1.29 kg/m3,动力黏度为1.48×10-5Pa·s。
1.3 网格划分
由于气膜厚度是微米级,文中利用有限元前处理软件ANSA强大的网格划分功能,在径向方向上将气膜共分成6层,并生成六面体结构性网格,随后进行网格独立性检验。为提升计算效率,确定网格数量为126万个结构性体网格。图2所示分别为网格整体和气膜厚度分层放大图。
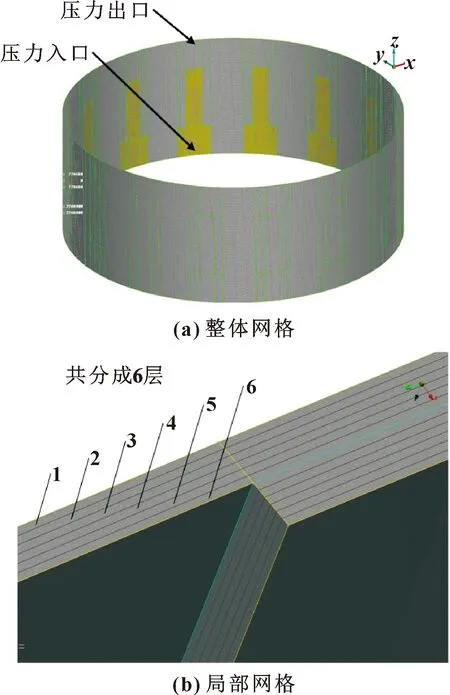
图2 气膜网格划分示意
1.4 边界条件设置
如图2(a)所示,文中选择T型槽宽槽处为压力入口,气膜坝区径向截面设置为压力出口,并设定出口压力为一个标准大气压,进出口压力差大小为0.1 MPa;无槽浮环设置为无滑移速度边界,有槽动环设置为旋转动态壁面,其转速大小为43.5 m/s。
1.5 流体运动状态判定
计算模拟引入如下假设:
(1)不考虑系统内流体的体积力和惯性力的作用。
(2)假定密封系统内与壁面接触的流体能保持壁面相同的速度,即不存在相对滑移速度。
(3)柱面气膜密封系统内气体介质符合牛顿黏性定律。
(4)不考虑动浮环所产生的微小形变。
密封系统内轴向方向流体的流动方式为Poiseuille流,周向方向的流体为Couette剪切流,其雷诺数的计算方法分别如公式(1)、(2)所示。
Poiseuille流动的雷诺数:
(1)
Couette剪切流动雷诺数:
(2)
式中:ρ为工作流体密度;h为特征尺寸,文中选择其为气膜膜厚;μ为流体动力黏度;vc和vz分别为周向和轴向速度。
其中轴向速度大小的计算公式使用王学良等[15]推导出的公式(3)。
(3)
由于实际工作中密封内流体在转速和压力的共同影响下,流体流动方式较为复杂,为判断流体流动方式,使用BRUNETIRE等[16]提出的判断方法:
(4)
当流动因子a>1时,则认为系统内流体流动状态为紊流;当α<0.562 5时,则认为系统内流体流动状态为层流。
使用前文所给出的相关参数,计算得到文中Rep和Rec分别为4.05和31.3。根据式(4)计算得α=0.020 07<0.562 5,因此文中流体运动状态为层流。
2 气膜流场数值分析与讨论
2.1 稳态性能计算方法
(1)平均气膜厚度
H0=(hmax+hmin)/2
(5)
式中:hmax指气膜厚度最大处的值;hmin指气膜厚度最小处的值。
(2)泄漏率
(6)
式中:Q代表泄漏率;Rj表示动环半径;p指气膜工作压力;θ是最大膜厚处的角向坐标。
(3)浮升力
(7)
式中:Ft为气膜周向切线方向分力;Fr为浮环径向分力;Fg为浮升力合力。
(4)气膜刚度
(8)
式中:F表示浮升力。
2.2 计算模型验证
为验证所建立的数值计算模型的准确性,在与文献[17]相同的参数设置下,研究气膜密封系统泄漏率随转速改变的情况,并与文献结果进行了对比,如图3所示。可以看出,文中模型的计算结果与文献得到的泄漏率变化情况一致,并且符合程度较高,验证了文中模型的正确性。
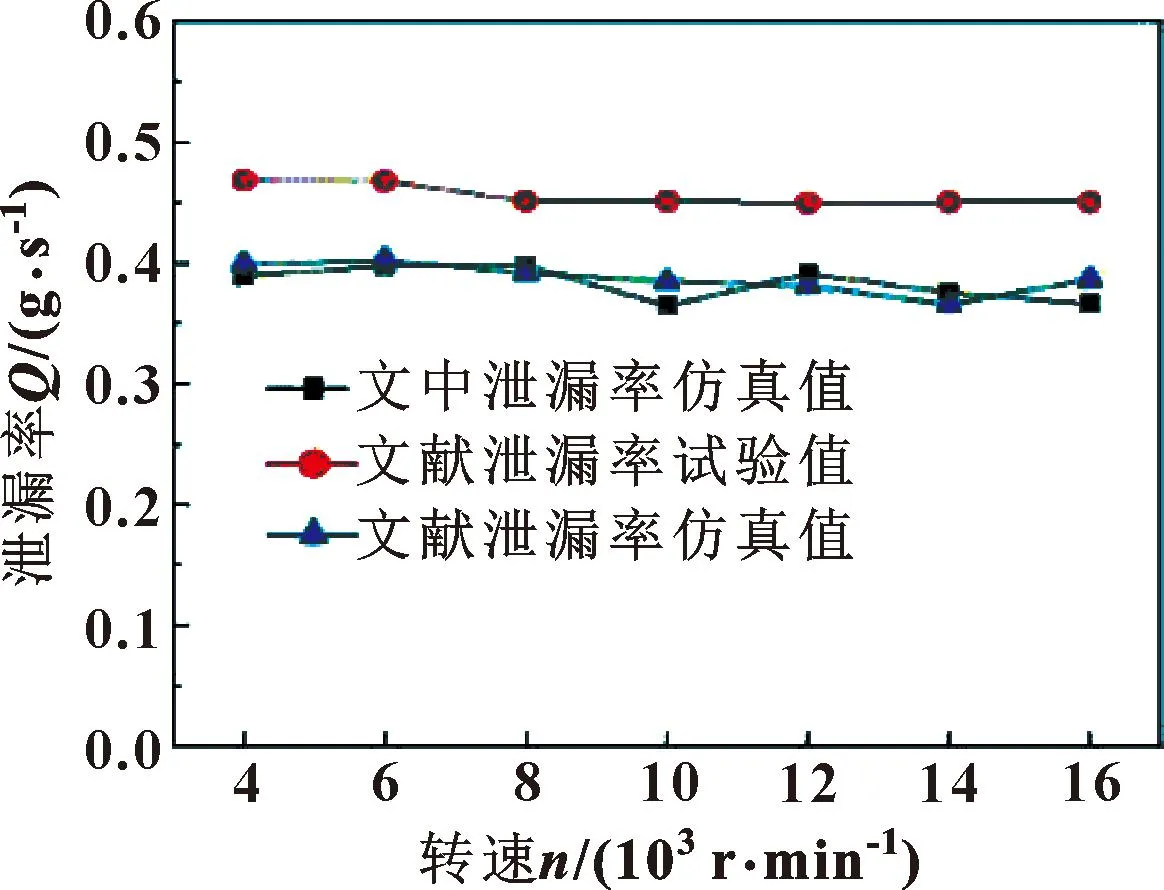
图3 不同转速下泄漏率比较
2.3 结构参数对泄漏率的影响
图4所示是转速8 000 r/min下,分别改变密封长度、T型槽槽数和槽深等结构参数,系统泄漏率的变化情况。可知,随着3种结构参数的增大,系统泄漏率整体变化并不明显。从图4(a)可看出,增大密封长度系统泄漏率呈现逐渐降低的趋势,但下降梯度非常缓慢,密封长度从28 mm到52 mm增大24 mm,而泄漏率下降值仅为7.5 mg/s。泄漏率下降是由于密封长度的增加会使得通道内流体行程增加,从而损失更多的能量。但相较于流体本身具有的动能,通道增长损失的能量很少,因此泄漏率下降的趋势并不明显。从图4(b)、(c)可知,增大T型槽槽数和槽深,系统泄漏率呈现上升趋势。在图4(b)中,T型槽槽数由10个增加至26个,泄漏率增加6 mg/s;在图4(c)中槽深度从5 μm到30 μm增大6倍,而泄漏率增加值为8 mg/s。这是由于柱面密封主泄漏存在于T型槽和浮环之间的区域,增加槽数和槽深会使得通道面积和数量增大,泄漏率随之提升。
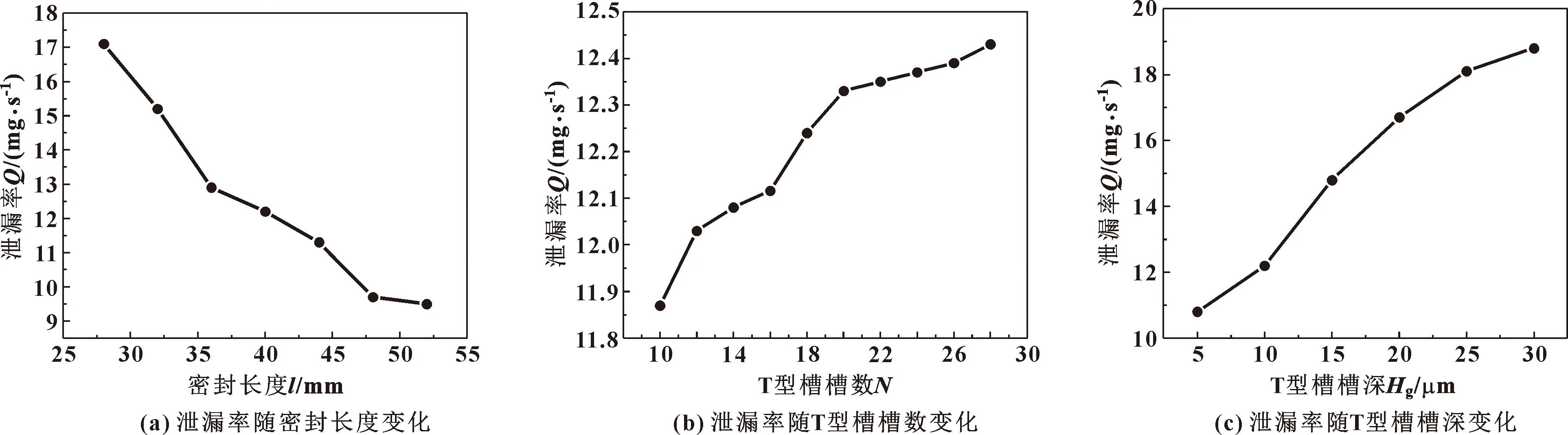
图4 结构参数对系统泄漏率的影响
2.4 结构参数对浮升力的影响
图5所示是转速8 000 r/min下,分别改变密封长度、T型槽槽数和槽深等结构参数,系统浮升力的变化情况。从图5(a)可以看出,系统浮升力大小随密封长度变化明显,密封长度从28 mm到52 mm增大24 mm,浮升力增加值为1 450 N,这是由于增加密封长度会增大通道面积,使得流体动压效应加强,从而导致浮升力上升。从图5(b)可知,随着T型槽槽数的增大浮升力逐渐上升,但趋势缓慢,T型槽槽数从10到26增加16个,系统浮升力增加值为13 N,说明T型槽槽数对系统浮升力的影响并不显著。这是因为T型槽槽数增加会使通道流体内压力加强,浮升力随之增大,但压力的增加较少,因此浮升力增大数值也不明显。从图5(c)可知,T型槽槽深从5 μm到30 μm增大6倍,系统浮升力增加值为290 N,可见槽深对系统浮升力有较大影响。这是因为T型槽槽深的增加会使得通道内流体动力润滑效应加强,使得槽型流体泵送能力加强,压力增大的同时浮升力随之增加。
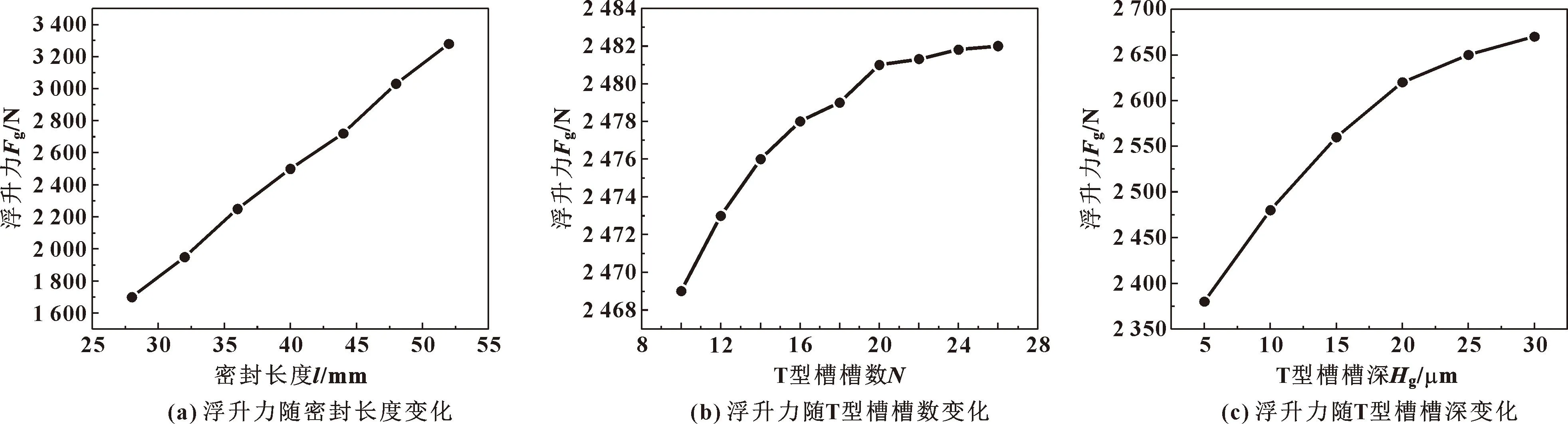
图5 结构参数对浮升力的影响
2.5 结构参数对气膜刚度的影响
图5所示是转速8 000 r/min下,分别改变密封长度、T型槽槽数和T型槽槽深等结构参数,气膜刚度的变化情况。从图6(a)可知,随着密封长度的增加,气膜刚度会随之缓慢增大,这是由于密封长度增加,密封流体动压润滑区域面积增大,气膜刚度得到提升。从图6(b)可知,T型槽数量从10到26增加16个,气膜刚度增大1.7×105N/m,这是由于槽数的增加,气膜动压效应增强使得气膜刚度增大。从图6(c)可以看出,随着T型槽深度的增加气膜刚度呈线性增长,T型槽深度从5 μm到30 μm增大6倍,气膜刚度增值为5.5×105N/m,可见T型槽槽深对气膜刚度有较大的影响。这是因为槽深的增加,槽内存在气体更多,流体动压效应加强,气膜刚度得到加强。
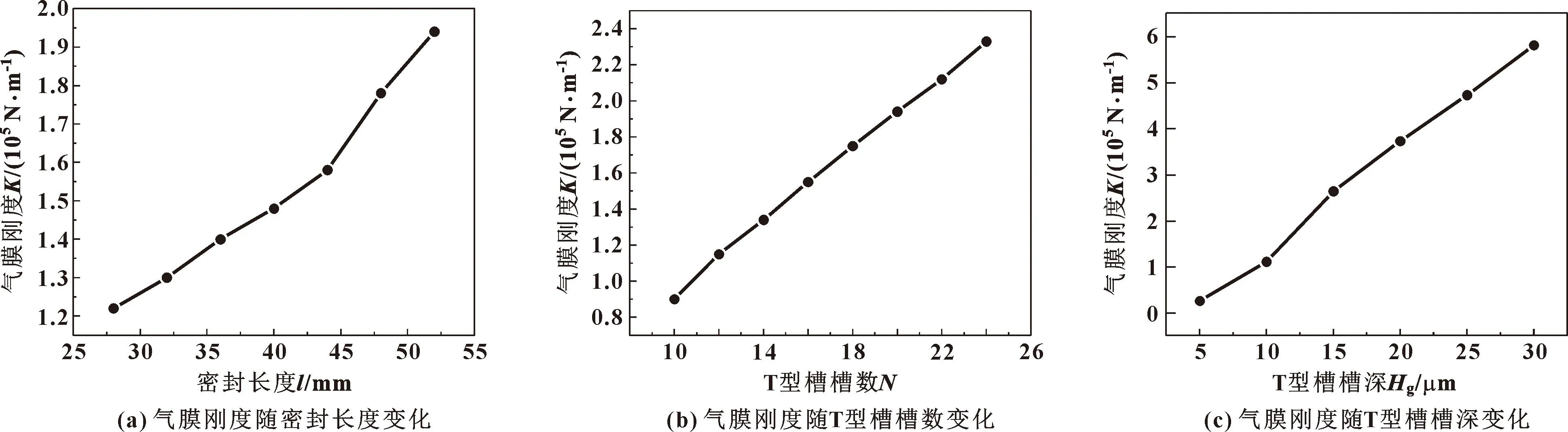
图6 结构参数对气膜刚度的影响
2.6 稳态性能多元非线性回归分析
在定工况下改变单一结构参数,使用多元非线性回归方程拟合结构参数与稳态性能之间的关系能够更直观地实现对稳态性能的预测。
2.6.1 公式拟合
根据数值计算结果,将稳态性能和结构参数表示成公式(9)所示的非线性组合形式:
(9)
式中:x1、x2、x3作为自变量分别代指T型槽槽深、T型槽槽数、密封长度;y为作为因变量的泄漏率、浮升力、气膜刚度;c0~c3为可变常数。
拟合得到的泄漏率与结构参数的函数表达式为
(10)
拟合得到的浮升力与结构参数的函数表达式为
(11)
拟合得到的气膜刚度与结构参数的函数表达式为
(12)
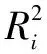
2.6.2 结构参数对密封性能影响程度判断
为得到各结构参数对稳态性能影响程度的主次顺序,采用计算偏回归系数的方法来判断,结构参数所对应的偏回归系数越大表明其影响越大。
偏回归系数Fj计算公式:
(13)
式中:Sj为偏回归平方和;Se为均方差。
(14)
(15)
其中Sa为和方差。将式(14)和(15)代入式(13)中,可得
(16)
其中
(17)
为方便计算对公式(10)左右两边取对数,并令lny1=Y1,lnx1=X1,lnx2=X2,lnx3=X3得到:
Y1=-8.877 5+0.387 61X1+0.040 92X2-
0.931 77X3
(18)
同理对公式(11)、(12)进行计算,得到各影响因素的偏回归系数Fj如表3所示。
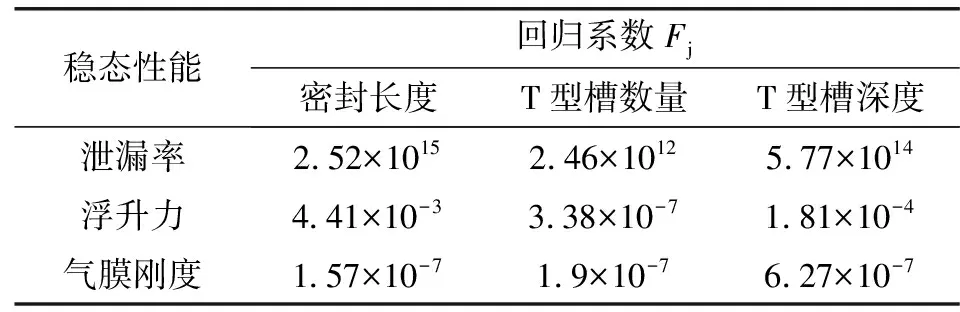
表3 各结构参数的偏回归系数
根据表1可知,密封长度对泄漏率影响最大,其次是T型槽深度,T型槽数量的影响最弱,因此为了降低系统泄漏率应优先考虑降低密封长度;密封长度对浮升力影响最大,其次是T型槽深度,T型槽数量的影响最弱,与前文仿真试验结果一致;T型槽深度对气膜刚度影响最大,其次是T型槽数量,密封长度的影响最弱,与图6所示的变化趋势相符。
3 结论
使用数值模拟的方法,研究了转速为8 000 r/min的工况条件下,结构参数对T型槽柱面气膜密封稳态性能的影响,并使用多元非线性回归分析拟合了稳态性能和结构参数之间的关系,判断出各结构参数对稳态性能影响程度的大小。主要结论如下:
(1)系统泄漏率随着密封长度增加而减小,T型槽数量和槽深的增加会使得泄漏率下降。影响系统泄漏率最大的因素为密封长度,其次是T型槽深度,T型槽数量影响最小。
(2)浮升力随着密封长度、T型槽数量和槽深的增加均呈现逐渐上升的趋势,其中影响最大的是密封长度,其次是T型槽深度,T型槽数量影响最小。
(3)气膜刚度随着密封长度、T型槽数量和槽深的增加均呈现逐渐上升的趋势,其中影响最大的是T型槽深度,其次是T型槽数量,密封长度影响最小。

