人工髋关节织构化表面摩擦学性能研究*

郝佳丽 郑清春 张春秋 张曌雄 付蔚华 胡亚辉

(1.天津市先进机电系统设计与智能控制重点实验室 天津 300384；2.机电工程国家级实验教学示范中心(天津理工大学) 天津 300384；3.天津医科大学总医院普通外科 天津 300052)

人工髋关节置换术是近代逐渐发展起来的一种治疗关节疾病的新技术，能够帮助患者减轻疼痛。但人工髋关节作为一种器官替代物，关节假体与自体之间的摩擦磨损几乎是不可避免的，这也是导致人工关节失效的最重要原因。

近年来，众多的学者致力于研究如何降低人工髋关节摩擦副间的磨损，其中研究的热点是在人工髋关节表面设计一定的微织构来提高关节假体的耐磨性。刘强等人[1]用激光器在铝合金表面加工出具有规则形貌的圆形凹坑，摩擦磨损实验表明，相较于无织构表面，微织构化表面磨损程度减轻。任荣杰和董光能[2]受自然界网络结构启发设计了3种连通的分叉沟槽型织构，即十字形、Y形和T形织构，通过摩擦磨损实验发现织构率在10%～20%的范围内，3种仿生树状网络织构的摩擦因数均低于无织构盘，有利于改善润滑状态。李亚军等[3]用激光加工的方法在45钢表面加工出不同面密度的凹坑织构，在干摩擦和乏油工况下对比了织构化试样与无织构试样的磨损率和摩擦因数，得出织构化提高抗磨性的真正原因在于凹坑的存在而不是摩擦因数减小。WEI等[4]认为微织构润滑模型的凹陷减少了摩擦副的实际接触面积，减小了黏着摩擦，在滑动状态下，凹坑可以较好地收纳磨粒减小磨损，还可以储存润滑液以供二次润滑。

目前的研究已经充分证明微织构的设计可以改善表面摩擦条件，并且织构形状、织构参数以及面积率都会影响摩擦副表面的摩擦润滑[5-8]。为了进一步研究人体在正常行走状态下织构形状对人工髋关节表面摩擦性能的影响，本文作者选择具有良好力学性能的钛合金和耐磨性强的氧化锆陶瓷作为人工髋关节配副假体材料，根据鲨鱼皮特殊的表观结构可以降低与水的摩擦在人工髋关节表面设计了仿生菱形织构，同时设计了圆柱形织构和圆环形织构，通过ANSYS Fluent对摩擦配副之间的流体域进行数值仿真模拟，比较3种微织构的摩擦学性能。

1 织构化表面流体动压模型建立及理论研究

1.1 微织构流域单元几何模型的建立

人工髋关节包含股骨和髋臼两部分，形状类似球形。微织构设计在股骨头表面，人工股骨头的尺寸为几十毫米，而微织构参数设计为微米级，数量级相差较大，因此可以忽略曲率的影响，将人工髋关节简化成准平面摩擦副，如图1所示。将织构化平面摩擦副之间的流体区域定义为微织构流域，取其中一个微织构流域单元进行研究[9]。

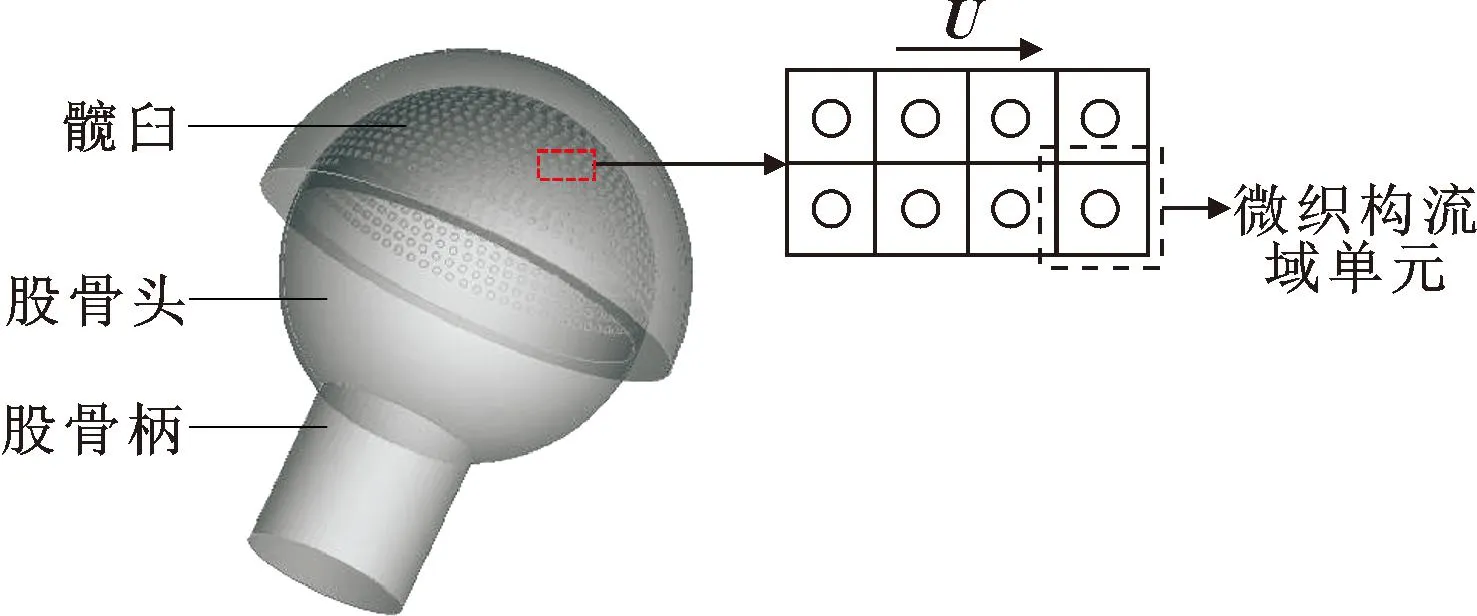
图1 织构化人工髋关节示意

用ANSYS前处理软件DM(DesignModeler)完成微织构流域单元的几何建模，微织构控制单元选用正方形，边长为L；初始油膜厚度为h0；仿生菱形织构边长为a，圆柱形织构半径为r，圆环形织构内半径为r1，外半径为r2；3种织构均为平底凹坑，织构深度为hp。微织构流域单元几何模型以及参数设计如图2所示。

图2 微织构流域单元几何模型示意

定义织构面积率Sp为控制单元内织构的开口面积S与控制单元面积之比，深径比λ为织构深度与织构沿滑动方向长度比值。公式如下：

(1)

(2)

1.2 流体动压润滑理论

1.2.1 雷诺方程的推导

雷诺方程是流体润滑研究的理论基础，在建立动压模型前需要进行以下假设：

(1)不考虑润滑液自身介质的重力影响；

(2)润滑液在摩擦副中的流动为层流，沿着膜厚方向的压力变化忽略不计；

(3)润滑液为不可压缩牛顿流体，沿润滑液流动方向，润滑液的黏度和密度为常数；

(4)润滑液与摩擦副表面之间无相对滑动。

则雷诺方程的一般表达式可以简化成[10]：

(3)

式中：η为润滑液的黏度，Pa·s；U为滑动速度，m/s；p为润滑油膜压力，Pa；h为油膜厚度。

摩擦副之间任意位置润滑液的膜厚h(x，y)为

(4)

式中：h0为初始油膜厚度，μm；hp为微织构深度，μm；Δ为不同形状的微织构凹坑区域。

1.2.2 微织构流体动压润滑机制

微织构在流体润滑下的作用机制如图3(a)所示。流体动压效应产生在微凹坑附近，润滑液流入微凹坑由于摩擦副表面间距变大形成发散楔，在发散区域压力形成了负压；润滑液流出微凹坑，表面间距变小形成收敛楔，在收敛区域压力突然升高形成正压，并且正压最大值高于负压最小值，导致在微凹坑边缘产生了非对称的压力分布，从而产生额外的承载力[11]。图3(b)所示为圆柱形织构在sp=25%、hp=20 μm、U=0.1 m/s情况下的油膜压力分布云图，可以看出仿真结果与理论结果相符合。

图3 微织构表面润滑膜流体动压产生示意

1.2.3 摩擦性能参数计算

在织构控制单元内分别将油膜压力p、表面剪应力τ对控制单元下壁面进行积分，得到油膜沿z轴方向的承载力F以及壁面沿x轴方向摩擦力Ff，之后通过计算得到摩擦性能参数平均承载力Fa和摩擦因数f，公式如下：

(5)

(6)

Fa=F/L2

(7)

f=Ff/Fa

(8)

1.3 仿真模型求解及主要参数设定

采用Fluent Meshing完成模型的边界条件设定，图4所示为圆柱形织构流域单元边界条件的设定。单元的上、下边界均设无滑移壁面边界条件，其中上边界滑动速度为U，方向沿着x轴，下边界为固定壁面；入口、出口边界设为平移周期边界条件；前、后边界设为对称边界条件。网格划分先要生成高质量的面网格，然后再生成体网格。为了确保求解的准确性，在进入Solution模式求解之前要检查网格质量，避免负体积网格生成从而影响后续求解。

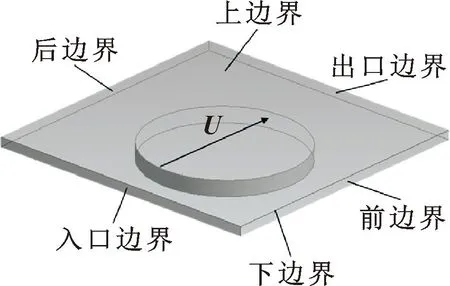
图4 微织构流域单元边界条件设定

文中研究稳态、层流情况下的微织构表面流体动压，润滑液介质选取不可压缩牛顿流体，黏度选取分子结构与人体蛋白类似的牛血清蛋白液黏度，即0.05 Pa·s。流场迭代算法采用SIMPLE压力速度耦合，压力离散选用PRESTO！，为保证求解的精度将残差值绝对标准设为1×10-5。

1.4 仿真结果验证

为验证仿真算法的可靠性，将无织构流域单元的剪应力理论值与仿真值进行比较。无织构壁面剪应力的理论公式[12]如下：

(9)

式中：速度梯度等于速度U与膜厚h0之比。

其中：润滑液的黏度取0.05 Pa·s；织构单元边长L=560.5 μm；初始膜厚h0为6 μm，对比结果如表1所示。

表1 无织构流域单元剪应力理论值与仿真值对比

由表1可知，在不同速度下理论值与仿真值误差小于3%，误差在合理范围之内，说明文中模型采用的仿真计算算法是可靠的，可以进行下一步的研究分析。

2 仿真实验设计

文中控制3种微织构流域单元织构的深径比λ=0.1，单个织构面积S=31 416 μm2，通过改变控制单元边长L达到调节面积率的目的。微织构所占控制单元的面积太小，微织构凹坑润滑液的存储量较小，所占面积太大会产生过小的坑间距使得摩擦副表面粗糙度增加，难以生成连续的润滑油膜，因此选取织构的面积率5%～25%进行研究[13]。滑动速度选取人体正常行走时髋关节与股骨头间的相对运动线速度即0.1～0.4 m/s[14]。其他织构参数与工况参数如表2所示。

表2 不同形状凹坑织构参数与工况参数

3 仿真结果及讨论

3.1 仿生菱形织构摩擦学性能分析

图5所示为不同速度下仿生菱形织构油膜平均承载力Fa与摩擦因数f随面积率的变化曲线。可以看出，随着面积率的增大，摩擦副之间的油膜平均承载力呈上升趋势，摩擦因数呈下降趋势，这与史于涛[15]通过摩擦实验得到的规律是一致的。在面积率为25%时平均承载力达到最大值，摩擦因数达到最小值。这是因为在所设面积率范围内，当织构所占面积增大，织构间的间距会相应地减小，在整个流体润滑过程中，产生了接触面积减少效应；而摩擦副表面的接触状态会影响其摩擦学特性，因此接触面积的减小起到了减小黏着摩擦力的作用，改善了摩擦条件[16]。

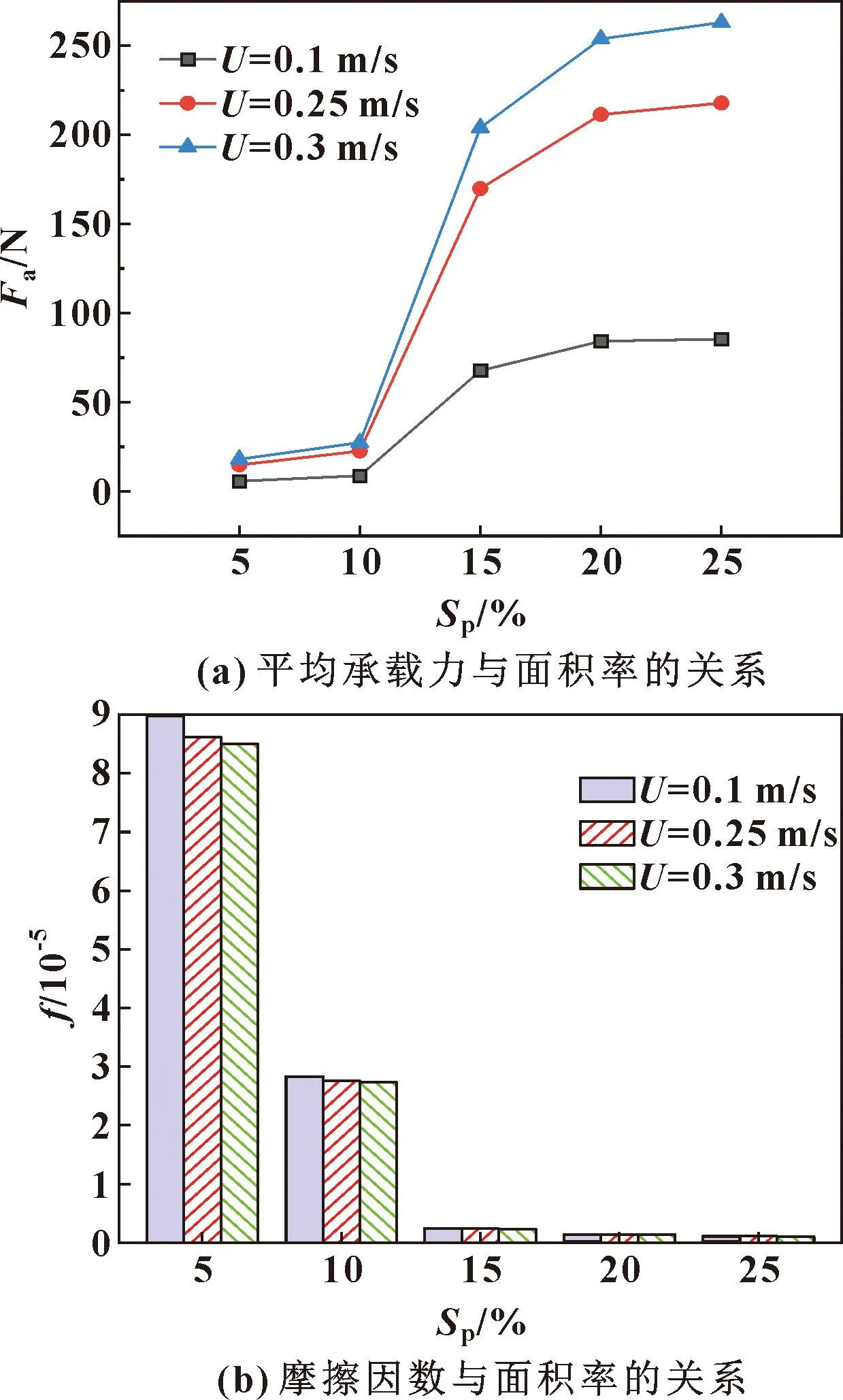
图5 不同速度下仿生菱形织构摩擦学性能

此外，在所设速度范围内，随着滑动速度的提高，平均承载力上升而摩擦因数降低，相同面积率下，滑动速度为0.3 m/s时平均承载力达到最大而摩擦因数达最小。这是因为当上表面滑动速度增加时，润滑液的流动速度也提高，这增大了润滑油膜的惯性力，压力沿x轴方向的正负压同时增大，但正压的增量要大于负压，增加了流体动压力进而提高了表面承载力和润滑膜刚度，实现了减摩作用[17]。

3.2 圆柱形织构摩擦学性能分析

图6所示为不同速度下圆柱形织构平均承载力及摩擦因数随面积率的变化曲线，发现曲线变化趋势与菱形织构相似。当面积率为5%时，油膜平均承载力最低，摩擦因数最大，且随着滑动速度的提高，平均承载力增大而摩擦因数逐渐减小，在U=0.3 m/s时达到最优润滑状态。当面积率Sp≥10%时，在滑动速度U=0.25、0.3 m/s下的摩擦因数基本相等。这是由于滑动速度提高到0.25 m/s时，摩擦副表面进入了完全润滑状态[16]，此时微织构产生的流体动压可以完全承担载荷，当速度继续提高时减摩效果不再提高。

图6 不同速度下圆柱形织构摩擦学性能

3.3 圆环形织构摩擦学性能分析

图7所示为不同速度下圆环形织构平均承载力及摩擦因数随面积率的变化曲线。从图7(a)可以看出，随着面积率从5%增大到25%，油膜平均承载力先下降后上升，在面积率25%达到最大。从图7(b)可以看出，摩擦因数随面积率增大呈下降趋势，在面积率25%时达到最小。对于平均承载力下降时摩擦因数也下降这一问题，杨小洋等[18]认为影响摩擦因素的因素有很多，平均承载力只是其一，面积率的变化会导致其他因素的改变进而影响摩擦因数。至于随着滑动速度的增加摩擦因数不减反增，跟圆环织构的几何特殊性有关，当滑动速度较大时，相比其他2种类型的织构，圆环织构上下摩擦副之间难以建立稳定而连续的润滑油膜，加剧了摩擦磨损，因此，滑动速度为0.25、0.3 m/s时的摩擦因数相比0.1 m/s有所上升，但上升幅度很小。

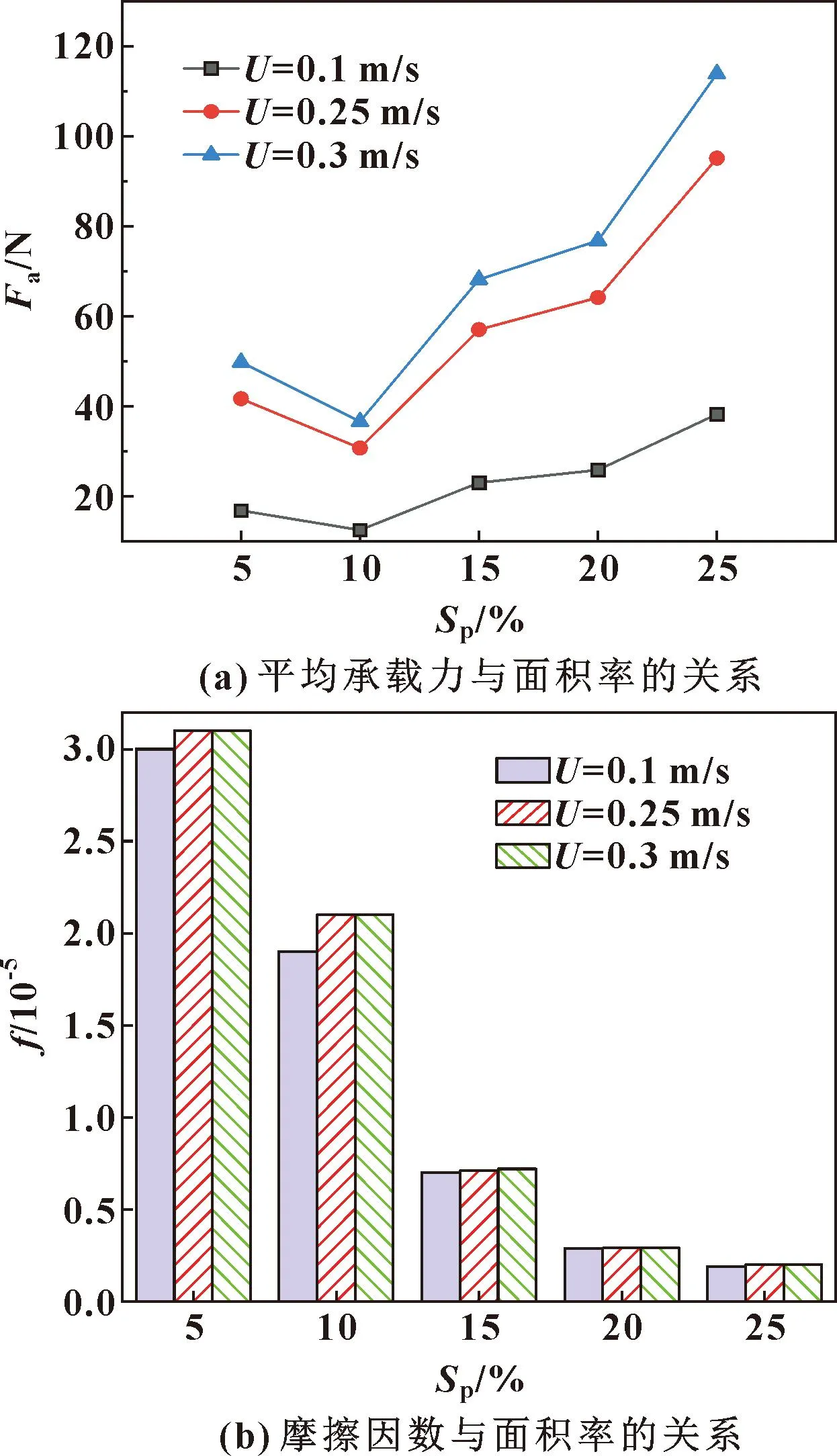
图7 不同速度下圆环形织构摩擦学性能

3.4 3种形状微织构摩擦学性能比较

由前文分析得到，在织构面积、深径比保持一定的情况下，每种微织构都存在摩擦学性能最佳的情况。为了进一步比较3种微织构的摩擦学性能，选择面积率为25%，对3种微织构的平均承载力和摩擦因数进行了对比，如图8所示。

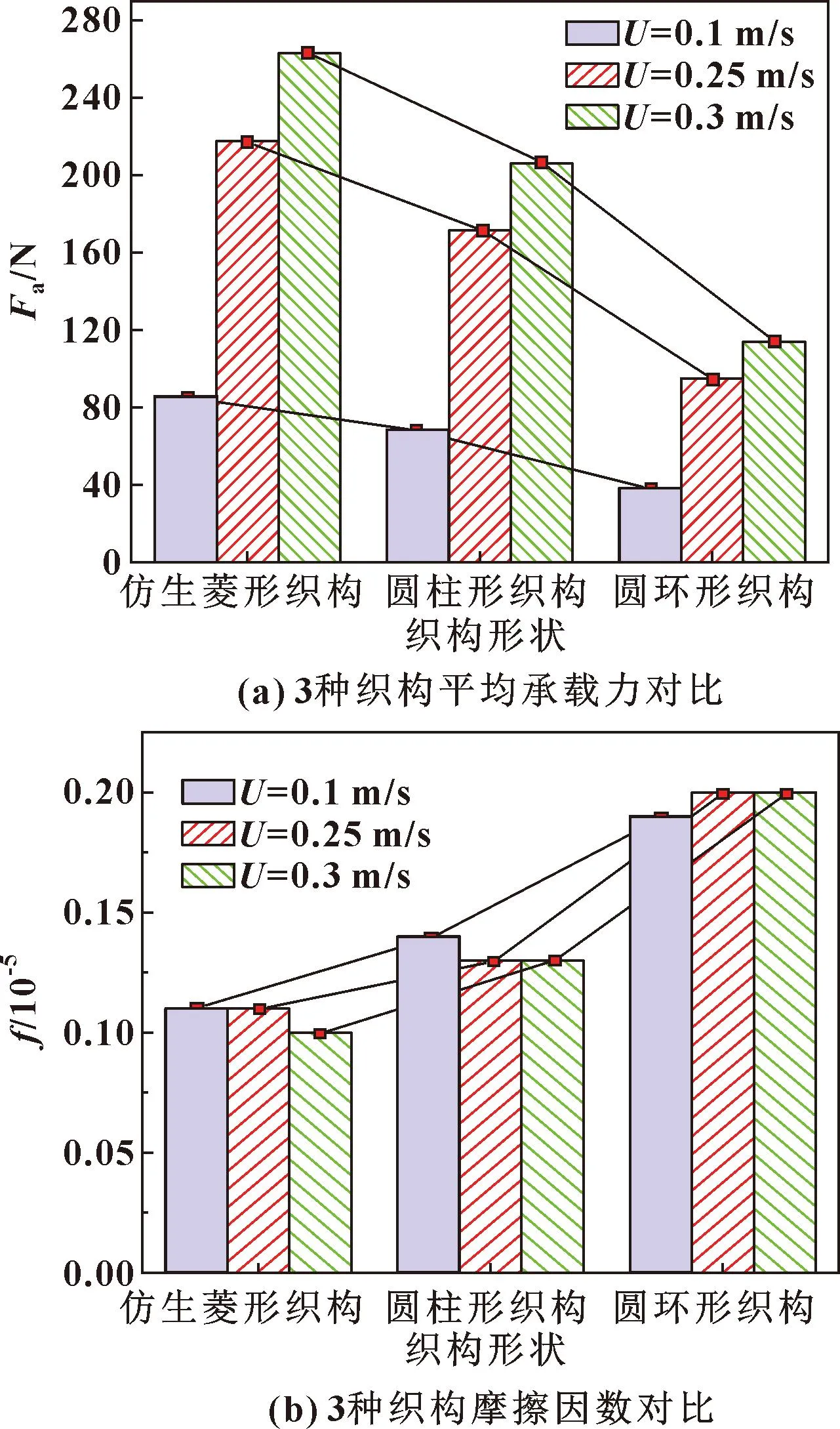
图8 不同速度下3种微织构摩擦学性能比较(Sp=25%)

从图8可以看出，在不同滑动速度下，仿生菱形织构的平均承载力最大，摩擦因数最小，因此仿生菱形织构的摩擦学性能最好[19-20]。由于圆柱形织构深度最深，织构内部的润滑液更容易形成涡流，涡流效应削弱了凹坑的动压承载性能。圆环织构摩擦学性能差是由于当设计单个织构的面积相同时，圆环织构的周长会更长，这将会导致接触应力对微织构边缘造成不利的影响，会破坏润滑油膜的连续性，加剧了摩擦副表面的磨损[21]。

4 结论

在人工髋关节表面设计了仿生菱形织构、圆柱形织构和圆环形织构，在流体动压情况下研究了3种织构对表面摩擦性能的影响，得到以下结论：

(1)在面积率5%～25%内，3种织构的油膜平均承载力随着面积率的增大而上升，摩擦因数随着面积率增大而下降，均在面积率为25%时取得最佳值。

(2)在0.1～0.3 m/s速度范围内，3种织构的油膜平均承载力随着滑动速度的提高而增大，在0.3 m/s时平均承载力达到最大值。而摩擦因数与滑动速度之间的关系随着织构形状不同存在一定差异。

(3)在面积率为25%时，3种织构中仿生菱形织构的摩擦学性能最好，圆环形织构最差，说明织构形状对表面的摩擦性能有一定的影响，因此合理选择织构形状在一定程度上可以提高油膜承载力，降低摩擦因数，从而改善人工髋关节摩擦副之间的摩擦磨损。