表面粗糙峰/谷对大滑滚比线接触热弹流润滑接触的影响*
王新庆 唐洪伟 王 静 杜恒瑞
(1.东华大学机械工程学院 上海 201620;2.青岛理工大学机械与汽车工程学院 山东青岛 266520)
大滑滚比工况(一般滑滚比大于2.0的工况)一般存在于滚珠丝杠[1]和无保持架轴承的相邻滚子或滚针[2]之间,或者平底凸轮-挺杆副[3]的接触中。在这样的接触中,两接触固体的表面速度方向是相反的,形成反向滑动工况。如果2个表面的速度大小相等,方向相反,则滑滚比为无穷;又因为卷吸速度为0,称为零卷吸工况。在该工况下,由于2个表面反向滑动,其剪切发热量大于一个表面滑动一个表面静止的工况。剪切发热造成表面携带出接触区的润滑油的温度高于带入接触区的温度,也就形成了接触区内润滑油的堆积,并形成由“温度-黏度楔”效应控制的接触区内凹陷油膜现象。该理论由英国帝国理工学院的CAMERON教授提出,经杨沛然教授发展和完善[4-5]。杨沛然和常秋英[5]还指出,在钢对钢接触的零卷吸工况下,接触区将形成左右对称的凹陷油膜。
ZHANG等[6-7]发现在大滑滚比工况下当表面速度降低时,由于低速表面携带入接触区的润滑剂流量降低,而剪切热产生的温升也不足以形成大的凹陷油膜,则产生较小的中央凹陷油膜;该凹陷油膜的深度和尺寸均随着表面速度的降低而进一步降低直至消失。唐洪伟等[8]在线接触大滑滚比工况下也发现了该现象。文献[6-8]研究还表明,随着表面速度的降低,油膜凹陷由大变小的过程由非牛顿流体效应控制。
以上研究均假设两表面绝对光滑,但实际接触表面由于加工原因会形成表面波纹度,或表面具有局部凸起或划痕,而表面波纹度、局部凸起或划痕都会对弹流接触区的油膜压力、膜厚和温升造成波动[9-11]。唐洪伟等[12]通过对大滑滚比条件下线接触热弹流润滑问题的数值仿真发现,表面波纹度的弹性变形随着滑滚比的增加而降低,其对压力和温升曲线造成的波动也随着降低。大滑滚比条件下粗糙表面的影响与纯滚动或滚滑工况下的热弹流问题完全不同,但对该类问题的研究并不多见。考虑到接触表面局部凸起或划痕的存在,本文作者假设在一个表面上存在单个粗糙峰或粗糙谷,研究随着滑滚比的增加,单个粗糙峰或粗糙谷对油膜压力、膜厚和温升的影响,研究结果对于揭示滚珠丝杠或无保持架轴承等的润滑油膜形成和失效有重要意义。
1 数学模型
文中研究采用Eyring本构方程[6-7]
(1)
式中:u为润滑油流速;τ为剪应力;τ0为Eyring流体特征剪应力。
Reynolds方程[7,13]为
(2)
式中:p为压力;h为膜厚;ua和ub分别是固体a和固体b的切向速度。
式(2)中的当量可以写为
方程(2)的边界条件为
膜厚方程[11]可写为
(3)
式中:Sa为粗糙度函数,其前面“-”号,代表粗糙峰,“+”号,代表粗糙谷。
假设x0为单个粗糙度的瞬时中心坐标,Aa为粗糙峰高度或粗糙谷深度,La为粗糙峰或粗糙谷宽度,则粗糙度函数Sa定义为
(4)
载荷由压力积分得到,其方程[7]为
(5)
润滑油黏度方程[7]为
(6)
式中:η0为环境黏度;T为温度;T0为环境温度,并且有
润滑油密度方程[7]为
(7)
式中:ρ0为环境密度。
油膜的温度方程[7]为
(8)
式中:c和k分别为润滑油的比热容和热传导系数。
方程(8)的温度边界条件为
式中:T0为环境温度。
对于固体a、b,两固体的速度恒为ua或者ub。两固体的能量方程[7]为
(9)
式中:ca、cb,ρa、ρb和ka、kb分别是固体a、b的比热容、密度和热传导系数;za、zb分别为固体a、b内与z同向的坐标。
方程(9)的温度边界条件[7]为
上面2个边界条件为在运动方向上的,下面2个为za、zb方向上的,式中d为两固体内变温层深度,计算中取3.15b,b为载荷w作用下的赫兹接触半径。
固-液界面热流量连续条件[7]为
(10)
为了便于求解及数值求解的稳定性,需对上述方程进行量纲一化,量纲一化参数定义如下
式中:u0为引入的速度参考量,其值大小对结果无影响。使用h作为膜厚方向坐标z的量纲一化参考量有利于对温度场的求解,在后面的结果分析中为了便于比较使用另一种量纲一膜厚H,其定义为H=(h/R)×105。
压力的计算采用多重网格法[14],弹性变形计算采用多重网格积分法[14],温度场的求解采用逐列扫描技术[15]。
2 结果及分析
计算中设置了4种滑滚比,分别为3.33、6、14和∞,各自对应着|ub|=ua/4,ua/2,3ua/4和ua。滑滚比越小,即2个表面的速度绝对值差别越大。当滑滚比为∞时,2个表面速度大小相等,方向相反,卷吸速度为0。
2.1 光滑表面弹流润滑分析
图1给出的是光滑表面弹流润滑分析的结果。图1(a)中的压力分布曲线表明,随着滑滚比逐渐增大,可以看到第二压力峰逐渐并入主峰,并使其明显增高;当滑滚比为无穷时第二压力峰完全消失。与压力曲线的变化相对应,图1(b)中膜厚分布曲线的表面凹陷也随着滑滚比的增加而逐渐加深,并且逐渐向接触中心处移动,最终在滑滚比为无穷时演化为左右对称的凹陷形状,油膜厚度增加。图1(c)所示是油膜中最大温升所在油层的温升曲线。由于压力功在温度升高中的重要作用,温升曲线和油膜压力曲线在形状上非常接近。上述油膜变化规律可以用“温度-黏度楔”机制[4-5]来解释:在两表面反向运动时,在接触区域左侧,表面a尚未进入接触区所以是冷的,其携带进入接触区的润滑剂黏度高,速度梯度小;表面b刚离开接触区所以是热的,其携带进入接触区的润滑剂黏度低,速度梯度大,从而有进入接触区的润滑剂数量多于离开接触区润滑剂数量的倾向。
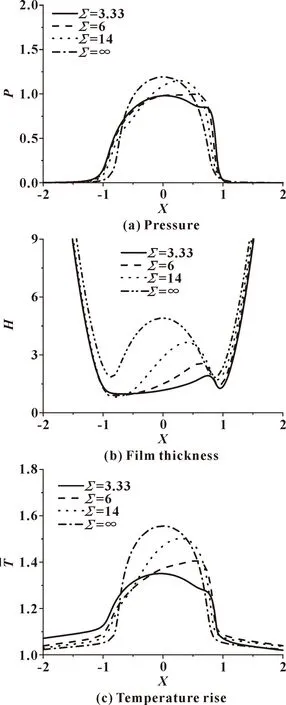
图1 滑滚比对光滑表面压力、膜厚和温升分布的影响
2.2 表面带单粗糙峰的弹流润滑分析
图2给出了不同滑滚比下表面a上带单个粗糙峰时的油膜压力、膜厚和温升分布,粗糙峰位于接触区入口部分,其中心坐标X0=-0.55,La=60 μm,Aa=0.2 μm。当滑滚比为3.33时,粗糙峰所在位置压力和温升曲线均有一个局部凸起,而膜厚有局部下降。随着滑滚比的增加,该粗糙峰对压力和温升曲线造成的凸峰高度逐渐下降,在滑滚比为无穷,也就是卷吸速度为0时,几乎看不出对压力和温升的扰动,对膜厚的扰动体现在膜厚仍有局部的下降。
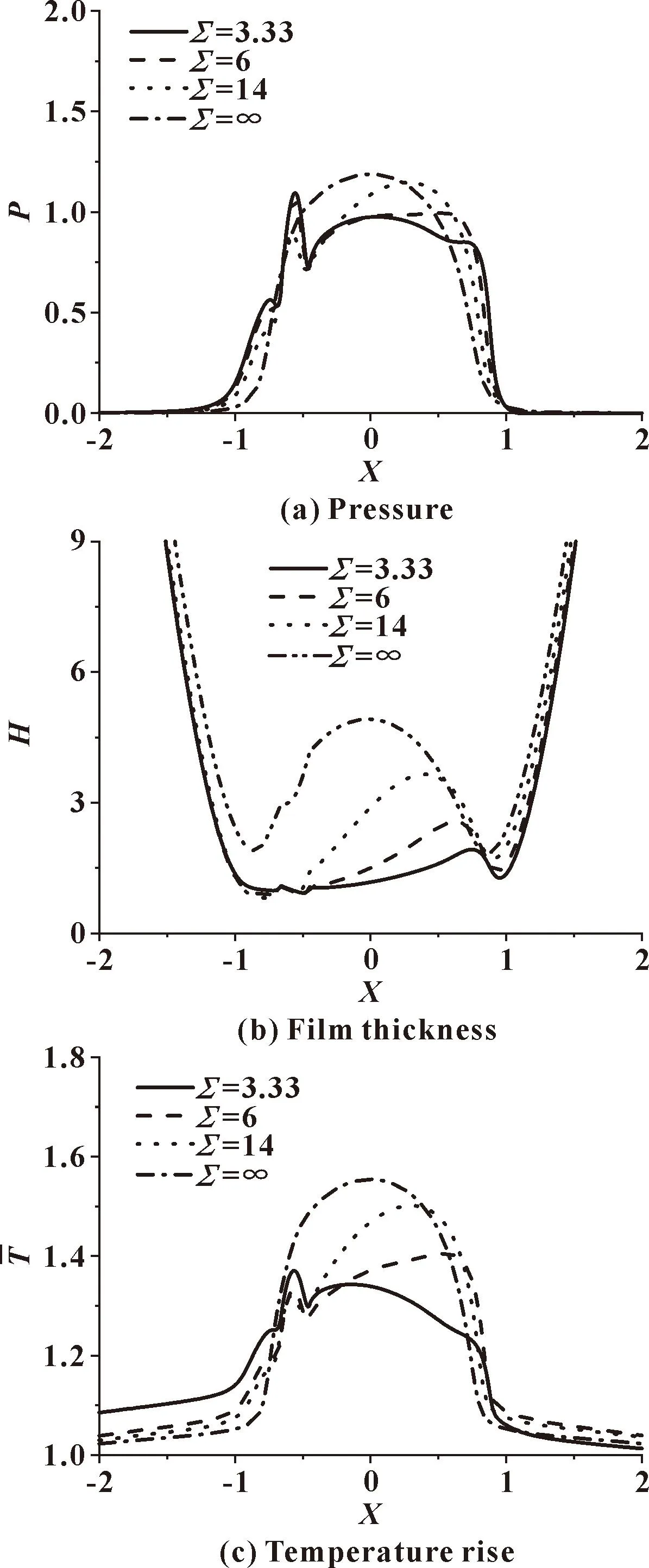
图2 入口位置粗糙峰对压力、膜厚和温升分布的影响(X0=-0.55,Aa=0.2 μm)
图3给出了当图2中的单个粗糙峰随表面运动到接触区出口位置X0=0.67时的结果,La=60 μm,Aa=0.2 μm。与图2类似,当滑滚比为3.33时,粗糙峰所在位置压力和温升曲线均有一个局部凸起,而膜厚有局部下降。随着滑滚比的增加,该粗糙峰对压力和温升曲线造成的凸峰高度逐渐下降。在两接触表面速度大小相等方向相反时,几乎看不出对压力和温升的扰动,对膜厚的扰动体现在膜厚仍有局部的下降。但与图2不同的是,在滑滚比未到达无穷时,粗糙峰对压力和温升曲线造成的局部波动幅度均小于图2,这是因为X0=0.67位置处的“温度-黏度楔”效应要强于X0=-0.55所在位置处。在两接触表面速度大小相等方向相反时,由于凹陷左右对称,接触区两侧的“温度-黏度楔”效应一致,所以此时2种情况下的压力、膜厚和温升曲线已经一致。
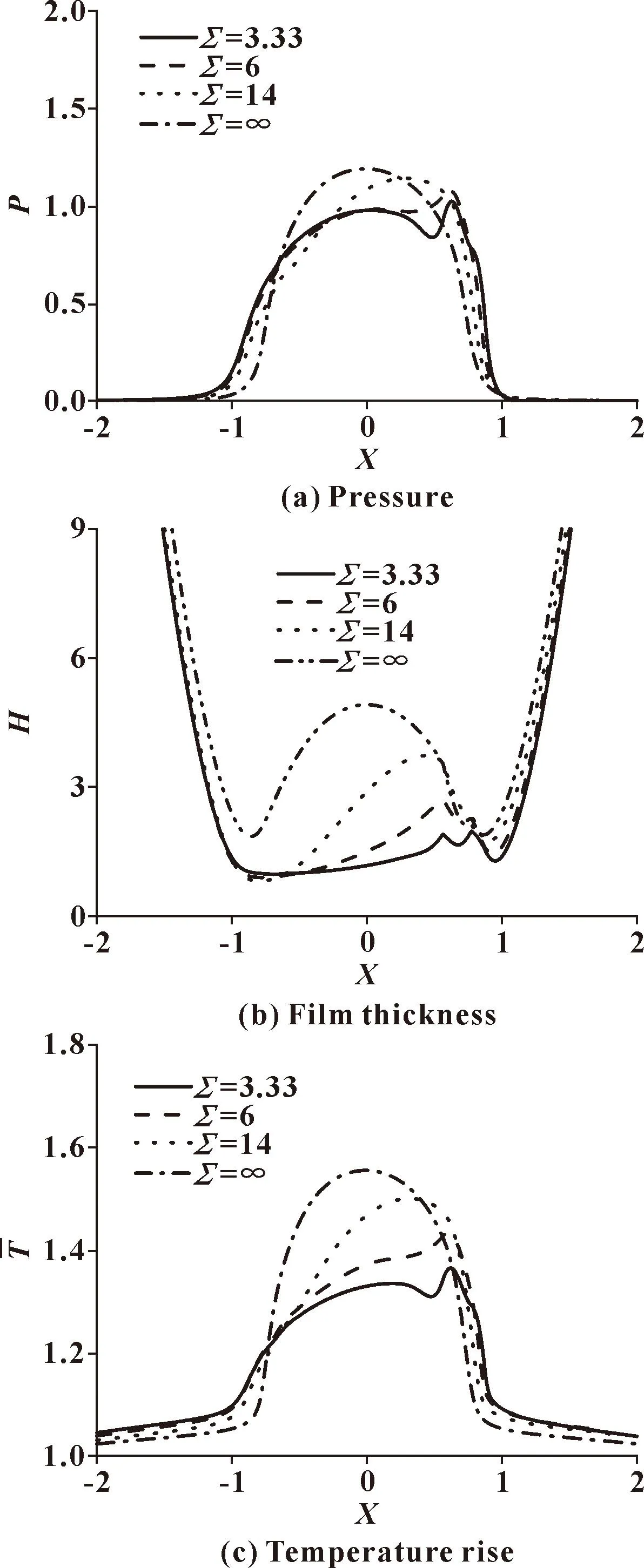
图3 出口位置粗糙峰对压力、膜厚和温升分布的影响(X0=0.67,Aa=0.2 μm)
图4给出了滑滚比3.33和∞条件下,粗糙峰幅值增加到0.5 μm时对油膜压力和膜厚的影响。粗糙峰位于接触区入口,X0=-0.55。由图4(a)可见,对于滑滚比3.33,粗糙峰幅值的增加导致了剧烈的局部压力波动,量纲一最大压力值增加到了1.53,是图2中最大压力的1.5倍。原因是在卷吸速度为0的条件下,“温度-黏度楔”效应形成了一个大的油膜凹陷,在这种条件下,表面粗糙峰对润滑油的流动形成的阻碍比较小。因此润滑油的流动不会在接触区遇到比较强的阻力,也就不会有显著的温升。由图4(b)可见,当滑滚比只有3.33时,接触区左侧粗糙峰所在处“温度-黏度楔”效应是比较弱的,因为油膜厚度比较薄,那么粗糙峰的存在对润滑油的流动就形成了强烈的阻力,造成压力的急剧升高。而当滑滚比为∞时,两表面反向滑动造成了强烈的温升,“温度-黏度楔”效应最强,接触区中形成了左右对称的油膜凹陷。所以粗糙峰所在位置的油膜本身是比较厚的。图4(c)给出了油膜中最大温升所在油层的温度曲线图。对于滑滚比3.33,油膜温升曲线在粗糙峰存在的位置也发生了剧烈的变化,而滑滚比为∞时的温升曲线几乎没有变化。对比图2和图4中不同滑滚比下的结果可知,随着滑滚比的增加,粗糙峰幅值增加对压力、膜厚和温升曲线造成的波动也逐渐减弱。
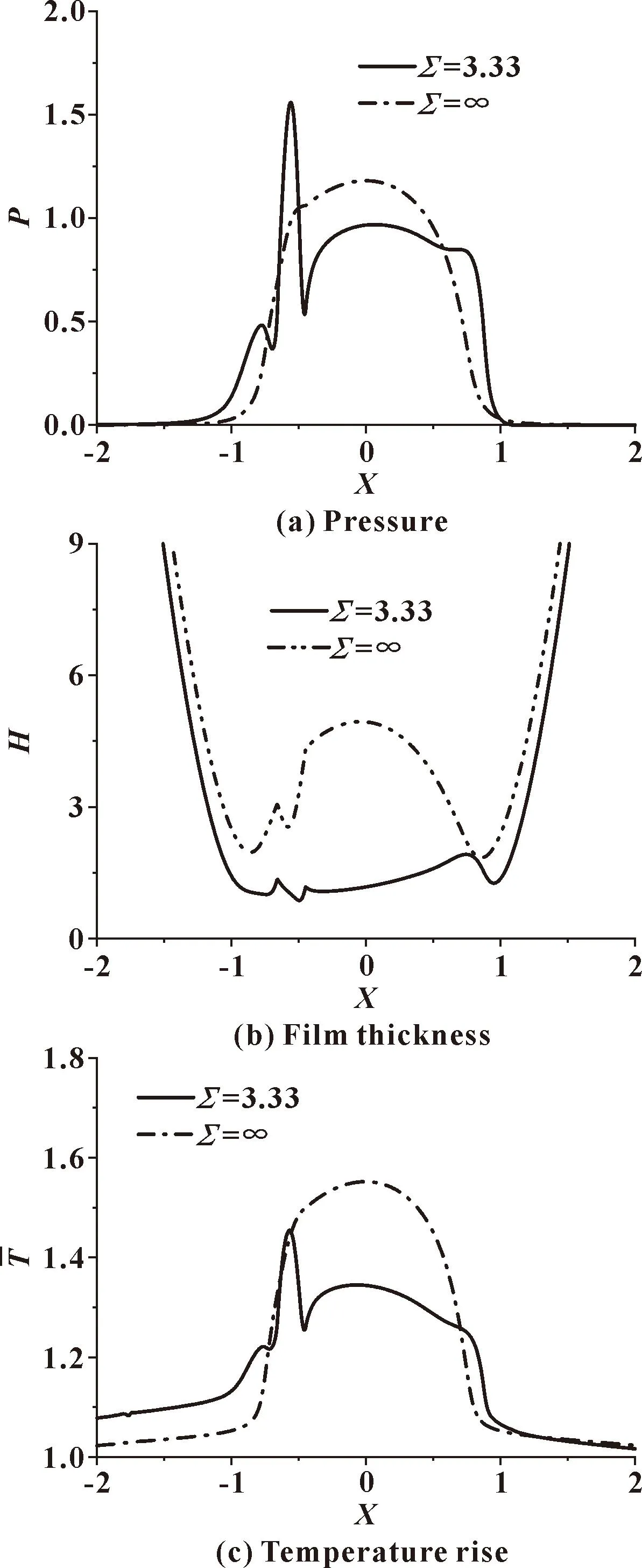
图4 粗糙峰幅值对油膜压力、膜厚和温升分布的影响(X0=-0.55,Aa=0.5 μm)
2.3 表面带单个粗糙谷的弹流润滑分析
图5给出了不同滑滚比下带单个粗糙谷表面的油膜压力、膜厚和温升分布,X0=-0.55,La=60 μm,Aa=0.2 μm。当滑滚比为3.33时,粗糙谷所在位置压力和温升曲线均有一个局部凹陷,而膜厚有局部增加。随着滑滚比的增加,该粗糙谷对压力和温升曲线造成的凹陷深度逐渐下降。在两接触表面速度大小相等方向相反时,也几乎看不出对压力、膜厚和温升的扰动。与图2相比,中心位置相同的粗糙谷对油膜压力、膜厚和温升曲线造成的局部波动幅度均小于相同幅值的粗糙峰,这是因为粗糙谷所在位置油膜是变厚的。
图6给出了不同滑滚比下带单个粗糙谷表面的油膜压力、膜厚和温升分布,X0=0.66,La=60 μm,Aa=0.2 μm。当滑滚比为3.33时,粗糙谷所在位置压力和温升曲线均有一个局部凹陷,而膜厚有局部增加。此位置粗糙谷对油膜的影响既小于图4中X0=-0.55位置的粗糙谷,也小于图3中相同位置粗糙峰的影响。随着滑滚比的增加,该粗糙谷对压力和温升曲线造成的凹陷深度也逐渐下降。在两接触表面速度大小相等方向相反时,也几乎看不出对压力、膜厚和温升的波动。图5和图6的结果说明,与图2和图3类似,随着滑滚比的增加,粗糙谷对压力、膜厚和温升的波动也是逐渐减弱的。类比于图4中的结果可预知,随着滑滚比的增加,粗糙谷深度增加对压力、膜厚和温升曲线造成的波动也将逐渐减弱,文中不再赘述。

图6 出口位置粗糙谷对压力、膜厚和温升分布的影响(X0=0.66,Aa=0.2 μm)
3 结论
(1)在大滑滚比条件下,表面存在单个粗糙峰或粗糙谷造成油膜压力、膜厚和温升曲线的局部波动。在滑滚比较小时,粗糙峰和粗糙谷对油膜压力、膜厚和温升曲线的影响较为明显,其影响随滑滚比增大而逐渐减弱,这是由于“温度-黏度楔”效应随着滑滚比的增加而增强。在大滑滚比条件下,由于凹陷油膜的存在,粗糙峰或粗糙谷都不会对润滑油的流动造成明显影响。
(2)在滑滚比较小的时候,由于接触区右侧的“温度-黏度楔”效应比接触区左侧的强,当粗糙峰或粗糙谷位于接触区左侧时,对油膜压力、膜厚和温升造成的波动较为明显。当粗糙峰或粗糙谷通过接触区,对油膜压力、膜厚和温升造成的影响则逐渐减弱。
(3)随着粗糙峰幅值的增加,在滑滚比较小的条件下,粗糙峰对压力、膜厚和温度曲线造成的波动显著增加。但是在两表面速度大小相等方向相反的工况下,粗糙峰幅值的增加对压力、膜厚以及温升曲线的影响也不再明显。

