素养导向下评价素材选择与教学启示
胡松


摘要:素养导向下的教学评价功能要在发挥数学思维内在力量的前提下,落实立德树人的根本目标.立足“教—学—评”一致性的课程理念,运用系统性思维,分析评价取向,整合教学内容,优化教学环节,“教对数学课”.
关键词:素养导向;评价素材;价值分析;教学启示
中考不仅考查学生基础知识、基本技能和基本方法,而且也常常用压轴题的形式考查学生运用数学思想方法分析问题和解决问题的能力.近几年,南京市中考压轴题有其独创性和前瞻性,笔者以其中部分试题为例,分析素材选取的特点,关注压轴题的所“压”之处,以供一线教师对课程的深度理解和育人方式的变革作参考.
1 素养导向下评价素材的选择
2022年版新课标指出要发挥评价的育人导向,关注学生数学核心素养培育的过程和结果[1].而选择较好的素材尤为关键,这里主要体现在两个方面,一方面可以结合核心素养的水平表现从知识维度来选择素材,一方面也要结合学生学习的过程、熟悉的情景等从问题解决角度来选择素材.
南京市这几年的中考压轴题从学生的学习生活出发,符合学生认知特点,读起来熟悉,上手不畏惧,同时又具有一定的思维深度和区分度,一定程度上对关注素养导向的评价做出了有意义的尝试.
1.1 素材来自课堂延伸处,压在铃声响起时
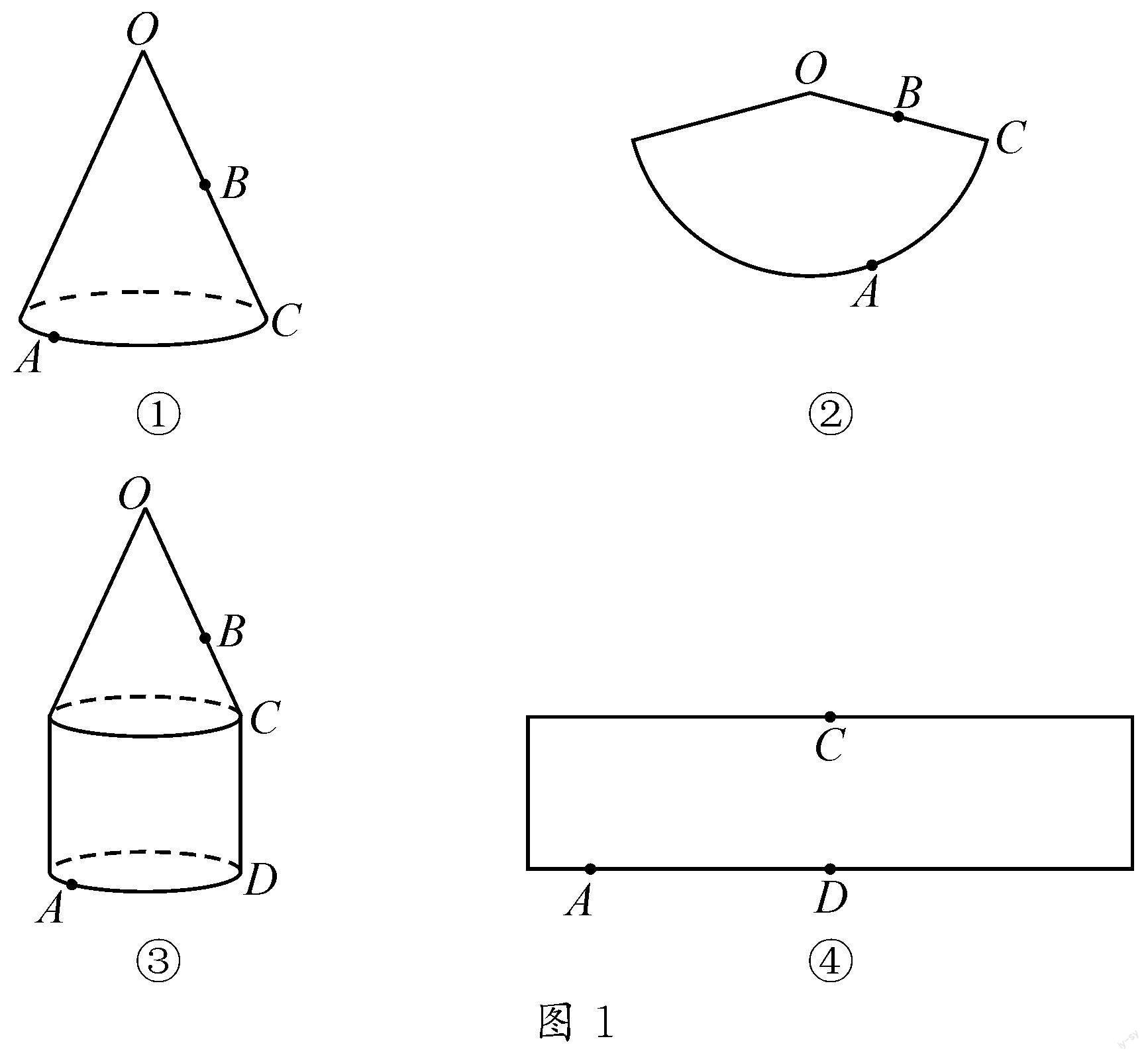
试题重现 (2021年·南京)在几何体表面上,蚂蚁怎样爬行路径最短?
(2)图1③中的几何体由底面半径相同的圆锥和圆柱组成.O是圆锥的顶点,点A在圆柱的底面圆周上.设圆锥的母线长为l,圆柱的高为h.
①蚂蚁从点A爬行到点O的最短路径的长为(用含l,h的代数式表示).
试题分析:我们常常有这样的体会,当铃声响起时,一个问题刚好讲完了,但是不是真的讲完了,学生是不是真的理解了我们想要表达的内容,无论是知识点,还是思想方法,他们能不能运用到其他场景中,会不会对我们所讲的内容进行进一步的思考.这也是铃声响起后,教师希望学生能够继续的内容.
“蚂蚁怎样爬路径最短”问题是个典例,通过展开立体图形的侧面或表面,从而把立体问题转化为平面问题,把折线段或曲线段转化为直线段,最后利用“两点之间线段最短”来解决问题.課堂上讨论的无非是蚂蚁在长方体、圆柱体和圆锥体表面爬行的问题,也可能是在这几个立体图形的相关元素,比如长方体的长宽高、圆柱体的高和底面半径上,进行一些一般性的讨论.当铃声响起时,学生常常终止了对这个问题的思考.而这类问题的解法是否可以运用到新的场景中去,应该是讲解这节课的价值所在.南京市这道压轴题正是延伸了这类问题的内涵,当铃声响起后,学生可以继续往下思考,如果蚂蚁是在一些简单几何体的组合体表面上爬行,这样的问题如何解决呢?题目由易到难地提出了两个问题,其中第(2)个问题的难度就在于是否真正能把“熟悉的解题方法”运用到“新的问题场景”中来,这有效考查了学生对这一模型的理解和应用,具有一定的挑战性.
1.2 素材来自在平时备课时,压在教材留白处
试题重现 (2018年·南京)结果如此巧合!
下面是小颖对一道题目的解答.
题目 如图2,Rt△ABC的内切圆与斜边AB相切于点D,AD=3,BD=4,求△ABC的面积.
解:设△ABC的内切圆分别与AC,BC相切于点E,F,CE的长为x.
根据切线长定理,得AE=AD=3,BF=BD=4,CF=CE=x.
根据勾股定理,得(x+3)2+(x+4)2=(3+4)2.
整理,得x2+7x=12.
小颖发现12恰好就是3×4,即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知△ABC的内切圆与AB相切于点D,AD=m,BD=n.
可以一般化吗?
(1)若∠C=90°,求证:△ABC的面积等于mn.
倒过来思考呢?
(2)若AC·BC=2mn,求证∠C=90°.
改变一下条件……
(3)若∠C=60°,用m,n表示△ABC的面积.
试题分析:很多中考试题,都可以在教材中找到原型.阅读教材,做教材中的习题,本质是为了让学生进行深度思考,培养思维能力和独创精神,在学习数学后能真正“聪明”起来,实现数学教育的“育人功能”.
2018年的这道压轴题的原型就是苏科版教材九年级上册第93页的第16题,教材中题目的条件和小颖解决的问题条件一样,只是求的不是面积而是内切圆半径.我们常遇到的求直角三角形的内切圆半径问题都是“已知两条直角边长,求内切圆半径”,而这个问题条件不一样,那么学生在解决教材这个问题的过程中,是不是可以思考一下,这个图形中还有哪些量是可求的,并将其写在教材的空白处,进而再思考,如果将题目中的长度和三角形的形状一般化,是否还可求解,而这就演变成了此压轴题中的问题.
1.3 素材来自学习过程里,压在典型习题中
试题重现 (2020年·南京)如图3,要在一条笔直的路边l上建一个燃气站,向l同侧的A,B两个城镇分别铺设管道输送燃气.试确定燃气站的位置,使铺设管道的路线最短.
(1)如图4,作出点A关于l的对称点A′,线段A′B与直线l的交点C的位置即为所求,即在点C处建燃气站,所得路线ACB是最短的.
为了证明点C的位置即为所求,不妨在直线l上另外任取一点C′,连接AC′,BC′,证明AC+CB<AC′+C′B.请完成这个证明.
(2)如果在A,B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域.请分别给出下列两种情形的铺设管道的方案(不需说明理由).
①生态保护区是正方形区域,位置如图5所示;
②生态保护区是圆形区域,位置如图6所示.
试题分析:为什么说这道题目压在典型习题中,因为初中三年的数学学习中有很多典型习题是学生一定会碰到的,这些典型的习题还会产生很多变式,从而形成一类典型问题.当问题的背景复杂化以后,学生要能从中抽象出相应的模型或方法,这是真正理解典型习题的关键.通过深挖这些典型习题,可以很好地考查学生对一个典型习题的多种变式及其拓展应用是否看清了知识的本质,是否能够触类旁通,思维的深刻性、广阔性和灵活性是否得到了很好的发挥和展现.
“将军饮马”问题就是初中阶段典型习题之一.在初中几何求最值问题中它通过与一些特殊图形结合,展现出了特殊的魅力.如,与直线、角、三角形、四边形、圆、直角坐标系中抛物线等函数图象的结合,在中考中都很常见.2020年的这道考题首先要求对“将军饮马”问题进行证明,考查学生对该典型习题的理解深度,不仅要知道方法,更要知道道理,体现数学是一门讲道理的学科.第(2)问的挖掘方向是在原来的线段中间加上障碍物,让“两点之间,线段最短”失效,在“经典”问题上开辟新问题,找准“经典”问题生长的源泉和动力,从而把一个比较“难”的问题,转化为比较熟悉的“简单”问题.
2 素养导向下评价素材选择的教学启示
中考试卷中的压轴题,具有一定的选拔功能,其目的就是要区分出学生的数学学习能力.中考试卷的亮点往往也在压轴题,体现对重要数学思想与方法等的考查.压轴题的综合性较强、难度比较大.在教学中,很多教师也认为,压轴题讲多了学生也听不懂,甚至是即使听懂了,稍微一变化还是不会做,因而他们选择放弃讲解压轴题,甚至直接忽略了压轴题.
从以上列举的南京市近几年的中考压轴题可以看出,压轴题并没有想象中那么可怕.首先,压轴题通常来源于课堂、教材、习题等学生熟悉的场景,在熟悉的问题和背景中进行挖掘,考查学生对课堂、教材、习题的理解深度;其次,这些题目来源于但是又高于
研究和討论过的问题,这就要学生养成爱提问题、爱思考的学习习惯.那么,如何提高学生的思维能力、培养爱思考的习惯就成为了教师日常教学中值得思考的课题.要培养学生良好的学习习惯,关键要“教对数学课”[2].
2.1 数学课要体现学科育人的价值
“教对数学课”首先要让数学课体现出学科育人的价值.我们的数学课应当不仅仅是停留在教授教材中的数学知识上,而应该是通过数学课培养和训练学生的多种数学思想,如类比思想、函数思想,以及优良品质,如勇于探索、百折不挠的品格等,体现出数学学科独特的育人价值.比如,在探究三角形全等条件的过程中,引导学生从三角形全等的性质出发,探究判断三角形全等究竟需要几个条件,进而尝试论证或举反例说明,形成几何学习的基本方法.那么,在研究三角形相似的条件时,学生就可根据学习全等的经验进行自主探究.
2.2 数学课要让学生养成主动思考的习惯
“教对数学课”其次要让学生养成主动思考的习惯.数学课的核心就是教学生学会思考,从本质上说就是要教学生学会提出问题,学会抽象概念,学会研究问题的一般方法.要让学生在学习数学的过程中不断地问自己几个问题:提出什么样的问题?问题从哪来?问题提出后如何解决?问题解决后有什么用?还以探索三角形全等的条件为例,在下课铃声响起后,鼓励学生探究四边形全等的条件,并找时间和学生一起讨论.这样的探究,不要认为是耽误时间,这种“慢”其实不是慢,而是为了弄清数学的本质,为了将来的“快”.
2.3 数学课要用好典型问题的模型
“教对数学课”还要用好典型问题的模型.当下,“题海战术”还是被不少教师认为是提高学生数学能力的法宝,即从大容量的题目训练中“悟”出解题的方法,“练”出解题的速度.在解题教学实践中,教师应当充分挖掘典型例题的教学功能,用好例题的典型性进行发散,用好例题的题设进行变式,用好习题的模型进行分解,培养学生分析问题与解决问题的立场、观点、方法.对于一个例题或者一个试题,如何拆解成能启发引导学生思考的一个个问题,是讲好题目的关键.课堂中教师的问题不仅是学习内容的载体,也是驱动数学课堂活动、完善知识结构、形成数学思想方法、获得活动经验的抓手.将典型例题中的图形、模型进行拓展,引发学生进一步思考,让这些思考呈现在教材、练习册的空白处,留给学生的思考空间就可以从课上延伸到课外[3].
压轴题并没有想象中那么高深莫测,在日常教学中,教师可以通过对教学内容的深度挖掘及教学方式的转变,把学习的时间和空间还一点给学生,鼓励学生学会思考,并且逐步养成在数学上敢于实践的勇气,这样会让学生乐于接受挑战,带着问题走进数学课堂,带着问题走出数学课堂,走向更广阔的天地.
参考文献:
[1]中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2011.
[2]余文森.有效备课\5上课\5听课\5评课[M].福州:福建教育出版社,2010.
[3]章建跃.构建逻辑连贯的学习过程使学生学会思考[J].数学通报,2013(6):5-8,66.

