数形结合思想在初中函数解题中的应用
姜静怡

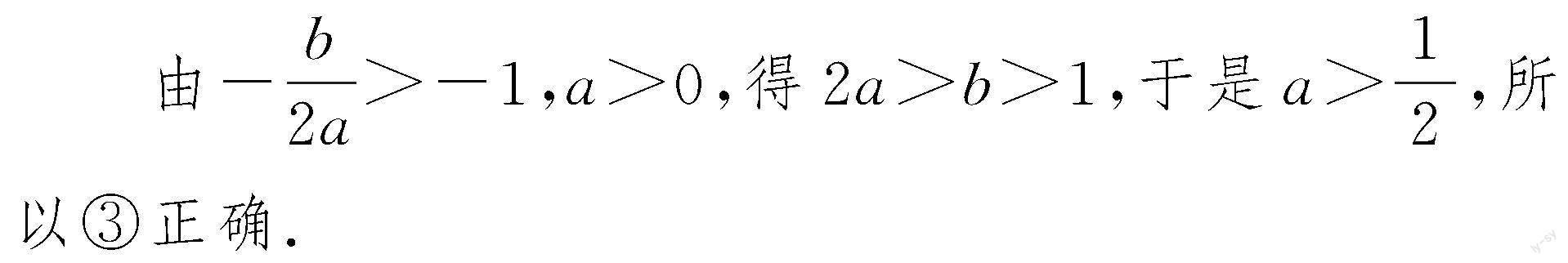

摘要:函数部分是中考考查的热点,也是初中数学教学的重难点.根据《义务教育数学课程标准(2022年版)》,中考关于函数考查的题目比例有所增加,其中应用数形结合思想解决的问题较多,给学生带来了一定的难度.本文中以此作为研究视角,立足初中函数解题教学,科学融入数形结合思想,借助图形的辅助,将抽象思维和形象思维结合起来,最终将复杂的函数问题简单化,帮助学生顺利解决相关函数问题.
关键词:初中数学;函数;数形结合思想
1 利用数形结合思想解决函数概念问题
学习函数,首先要明确函数的概念.这就要求学生能识别简单实际问题中的常量、变量及其意义;能根据函数图象分析出实际问题中变量的信息,发现变量间的变化规律;能结合函数图象分析简单实际问题中的函数关系,进而能初步推测变量的变化趋势.
例1 最近长春市连降雨雪,某水库水位上涨.图1表示某一天的水位变化情况,0时的水位为警戒水位.结合图象判断下列叙[JP]述不正确的是().
A.8时水位最高
B.P点表示12时水位为0.6 m
C.8时到16时水位都在下降
D.这一天水位均高于警戒水位
解析:本题是一道典型的运用數形结合思想解决函数概念的问题.解题时要在具体情景的基础上认真审题,结合题目给出的图象分析得出答案.
对于A选项,通过观察图象可知,在8时图象纵坐标最大为1.0.所以A选项正确.
对于B选项,在图象中可以观察到,P点对应的横坐标为12,纵坐标为0.6.所以B选项正确.
在C选项中,提到了从8时到16时的水位问题.通过观察图象可以发现,从8时到12时水位确实在不断下降,但从12时到16时水位没有发生变化.所以C选项错误.
D选项中提到这一天水位均高于警戒水位,即高于0时水位,观察图象可知D选项正确.
在解决本题时,教师要提醒学生运用数形结合的思想将图象与题干对应的信息联系起来,进而轻松解决问题.
2 利用数形结合思想解决一次函数问题
在学习一次函数的过程中,要十分注意数形结合思想的运用.要会画一次函数的图象,能根据图象和表达式y=kx+b(k≠0)探索并理解k>0和k<0时图象的变化情况,并且能够根据已知条件结合以往学过的知识解决实际问题.
例2 已知正比例函数y=2x的图象上有一点B(m+2,m2-4),且点B在第一象限.
(1)求点B的坐标;
解析:(1)通过数形结合思想,利用待定系数法将点B的坐标代入正比例函数解析式,解方程即可求得m的值.将点B(m+2,m2-4)代入正比例函数解析式y=2x,得到2(m+2)=m2-4,解得m=4或-2.又因为点B在第一象限,所以m=4.故点B的坐标为B(6,12).
(2)算出△OBC的面积为36,结合正比例函数解析式设点P(a,2a),分两种情况讨论.
当点P在线段OB上时,过点P作PD⊥BC于点D,如图2,
则PD=6-a.
当点P在射线BA上时,过点P作PD⊥BC交BC的延长线于点D,如图3,则PD=a-6.
综上,点P的坐标为(3,6)或(9,18).
3 利用数形结合思想解决二次函数问题
在初中函数的学习中,二次函数既是重点也是难点,更是中考的热点.中考对于二次函数考查的难度也在不断增加,在解题中,要不断融入数形结合思想才可以更加顺利地解决相关问题[1].关于二次函数,主要考查其图象问题,包括图象的开口方向、对称轴以及二次函数的最大值和最小值并确定相应的自变量的值,在此基础上还要能够解决简单的实际问题.学生在学习时要更加关注二次函数解析式中各个字母代表的含义.
A.①②
B.②③
C.②④
D.③④
当x=1时,由图象知y=2,代入解析式得a+b+c=2,所以②正确.
当x=-1时,y=a-b+c<0;由(a+b+c)-(a-b+c)>2,得b>1,所以④错误.
综上所述,B选项正确.
4 利用数形结合思想解决反比例函数问题
反比例函数作为初中函数的重要组成部分,主要考查其函数解析式及函数图象的应用,明确当k<0和k>0时反比例函数图象的整体特征,并能基于此解决实际问题.反比例函数知识点经常与一次函数和二次函数相结合,并且解题方法也相对比较特殊.经常借助交点求解三角形的面积.
(1)求k的值及点C的坐标;
(2)在y轴上有一点D(0,5),连接AD,BD,求△ABD的面积.
总而言之,函数是初中数学学习的一个难点,它也是考试的重点.对于学生在解决函数问题的过程中经常出现的一些错误,要给予他们足够的引导和启发,在解答问题的时候,将数形结合思想与问题直观融合起来,利用图形的帮助,将抽象、复杂的函数问题形象地展示出来,以便让学生能够更好地理清解题思路,从而更好地完成问题的解答.与此同时,在数形结合思想的帮助下,学生也实现了对数学知识的内化,推动了数学思维的发展,从而数学综合素质也得到了提高.总之,数形结合思想的合理应用,对于初中数学函数解题具有很大帮助.因此,具体教学中,教师应根据实际情况,引导学生通过合理的数学思维进行解题.这样才可以获得更好的教学效果,促进初中生数学学科的良好学习与发展[2].
参考文献:
[1]杨远鸿.数形结合思想在初中数学解题中的应用——以初中函数问题为例[J].数理天地(初中版),2023(1):52-53.
[2]曹峰.初中数学解题中的函数思想应用策略[J].数理天地(初中版),2023(9):26-27.

