分析错因,纠正错误,寻找方法
赵玉兰


在初中几何教学中,我们经常看到学生有一些似是而非的证法:有的是没有完全理解题意,有的是理由不充分,有的是以偏概全、以局部代替整体,有的是误解或误用了性质、定义、定理、公式,有的是作图误导,还有循环论证、偷换概念、推理步骤不规范等多种错误.教师如果能够弄清学生产生这些错误的原因,及时给予纠正或作为典型例题进行讲解,就能帮助学生在今后的学习中尽量避免或减少这些错误的发生.下面笔者列举了一些证明三角形全等的错例,侧重错因分析与正确证明的比较,供学生学习时借鉴、参考.
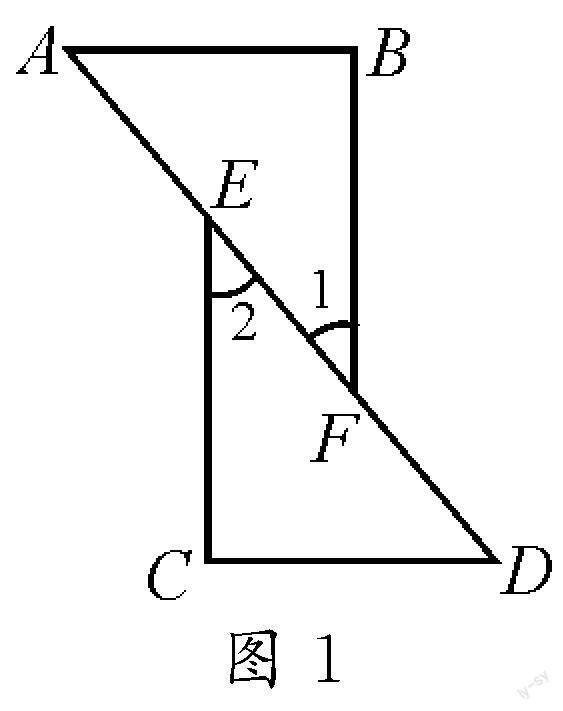
例1 如图1,已知点A,E,F,D在同一直线上,且AE=DF,CE=BF,CE∥BF.求证:AB=CD.
错证:在△ABF和△DCE中,CE=BF,AE=DF.
∵CE∥BF.
∴∠1=∠2.
∴△ABF≌△DCE(SAS).
∴AB=CD.
错因分析:错证犯了“以局部代替整体”的错误.在AE=DF中,AE是AF的局部,DF是DE的局部,绝不能因为AF,DE有公共部分EF,就以局部相等来代替整体相等.
正确证明:∵AE=DF,EF=FE,
∴AE+EF=DF+FE,即AF=DE.
又∵CE∥BF,
∴∠1=∠2.
∴△ABF≌△DCE(SAS).
∴AB=CD.
例2 已知AD和A′D′分别是△ABC和△A′B′C′的中线,AB=A′B′,BC=B′C′,AD=A′D′.
求證:△ABC≌△A′B′C′.
错证:如图2,
∴BD=B′D′.
在△ABD和△A′B′D′中,AB=A′B′,BD=B′D′,AD=A′D′,
∴△ABD≌△A′B′D′(SSS).
同理,△ADC≌△A′D′C′.
∴△ABD+△ADC≌△A′B′D′+△A′D′C′.
即△ABC≌△A′B′C′.
错因分析:错证犯了两个错误.第一是用了不合理的“同理”,△ADC≌△A′D′C′与△ABD≌△A′B′D′的理由不相同,要证△ADC≌△A′D′C′,须证∠ADC=∠A′D′C′,根据“SAS”来证;第二是由两对全等三角形之和推出△ABC≌△A′B′C′的理由不充分,倘若两对三角形不具备对应位置相同的条件则不全等,例如图2(1)与图3中,虽有△ABD≌△A″B″D″,△ADC≌△C″B″D″,但△ABC与△A″B″C″并不全等.
正确证明:
∵AD和A′D′分别是△ABC和△A′B′C′的中线,
∴BD=DC,B′D′=D′C′.
∵BC=B′C′,
∴BD=B′D′.
又∵AB=A′B′,AD=A′D′,
∴△ABD≌△A′B′D′(SSS).
∴∠BAD=∠B′A′D′,
∠B=∠B′.
在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,BC=B′C′,
∴△ABC≌△A′B′C′(SAS).
例3 如图4,AC与BD相交于点E,AD=BC,∠C=∠D.求证:AC=BD.
错证:连接AB.
∵AD=BC,∠C=∠D,AB=AB,
∴△ABD≌△BAC(SSA).
∴AC=BD.
错因分析:错证的原因是应用了“边边角(SSA)”这个假定理.为什么说它是假定理呢?请看图5,将等腰三角形ABC的底边BC延长线上的任一点D和顶点A相连,在△DAB和△DAC中,
满足AB=AC,AD=AD,∠D=∠D,但这两个三角形显然不全等.
正确证明:在△AED和△BEC中,∠AED=∠BEC,∠D=∠C,AD=BC,
∴△AED≌△BEC(AAS).
∴AE=BE,DE=CE.
∴AE+EC=BE+ED,即AC=BD.
例4 有两角和一边分别相等的两个三角形全等吗?若全等,则给出证明;否则,请举出反例.
错证:如图6,在△ABC和△A′B′C′中,根据条件不同可分为两种情况进行证明.
(1)∵∠A=∠A′,∠B=∠B′,BC=B′C′,
∴△ABC≌△A′B′C′(AAS).
(2)∵∠B=∠B′,∠C=∠C′,BC=B′C′,
∴△ABC≌△A′B′C′(ASA).
综上,有两角和一边分别相等的两个三角形全等.
错因分析:本题的证明过程看似无懈可击,而且把两种情况(AAS,ASA)都考虑到了.但仔细分析后发现仍然错误,其原因是把命题中的“分别相等”当成了“对应相等”.实际上,如图7,在△ABC,△A′B′C′,△A″B″C″中,虽然∠A=∠A′=∠A″,∠C=∠C′=∠C″,BC=A′C′=A″B″,但它们却不全等.因此,结论应是不一定全等.
例5 有两边和一条高对应相等的两个三角形全等吗?若全等,则给出证明;否则,请举出反例.
错证:全等.证明如下.
当高是对应相等的两边中一边上的高时,如图8,在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,CD和C′D′分别是边AB和A′B′上的高,且CD=C′D′.
在Rt△ACD和Rt△A′C′D′中,AC=A′C′,CD=C′D′,
∴Rt△ACD≌Rt△A′C′D′.
∴∠A=∠A′.
在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,AC=A′C′,
∴△ABC≌△A′B′C′.
当高是第三边上的高时,如图9,在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,AD和A′D′分别是BC和B′C′边上的高,且AD=A′D′.
在Rt△ACD和Rt△A′C′D′中,AC=A′C′,AD=A′D′,
∴Rt△ACD≌Rt△A′C′D′.
∴∠CAD=∠C′A′D′.
同理可证∠BAD=∠B′A′D′.
∴∠BAC=∠B′A′C′.
又在△ABC和△A′B′C′中,
AB=A′B′,∠BAC=∠B′A′C′,AC=A′C′,
∴△ABC≌△A′B′C′.
错因分析:本题的证明过程看似把两种情况都考虑到了,但忽视了“三角形的高不一定在形内”这种可能性.例如,若两个三角形一个为锐角三角形,另一个为钝角三角形,如图10中的△ABC与△ABC′,虽然AB=AB,AC=AC′,且它们第三边上的高都是AD,但显然这两个三角形并不全等.因此,结论是不一定全等.
综上可知,学生在证明过程中会出现各种各样的错误,这是一种正常现象,是学生思维过程的真实反映.在实际教学中,教师要帮助学生找到错误并分析产生错误的原因,并将学生的这种错误作为一种资源,因势利导,正确、巧妙地加以利用,纠正错误,使学生尽可能地减少错误,最终找到正确的方法,提高学习效率.

