嵌入式共固化阻尼复合材料圆板的振动分析

纪胜飞，梁森，孙兴帅，马国瑞

(青岛理工大学机械与汽车工程学院，山东青岛 266520)

0 前言

近年来，技术变革越来越依赖新材料的发展，作为未来发展方向之一的复合材料也得到了更多的应用和推广。其中，嵌入式共固化阻尼结构作为复合材料的代表，它是由不同性质的材料克服单一材料缺陷、发挥各自材料优势复合而成的一种多相固体，具有阻尼性能优异、抗老化、不脱落、耐疲劳等优点[1-2]，而且圆板结构作为机械工程中最基本的结构单元，被广泛应用于航空航天、船舶工业、仪器仪表等领域，因此对嵌入式共固化阻尼复合材料圆板结构的研究具有广泛的应用前景。

ROSE等[3]提出了一种黏弹性夹层结构模型，用于分析黏弹性层对结构振动性能的影响和动力响应。后来对夹层结构的研究主要集中在有限元与实验研究。DI SCIUVA[4]利用正交各向异性的较厚层合板的非线性运动方程研究了复合材料板的振动；后来，DI SCIUVA[5]运用连续性假设并建立模型来实现有限元方法的发展。ROY、 GANESAN[6]提出了一种约束阻尼层处理的圆板振动和阻尼分析的有限元方法。 FARAG、 PAN[7]利用数值模拟方法研究了各向同性薄板的面内自由振动和模态特性。李烜等人[8]以丁基橡胶为主要原料，利用模压法制得阻尼薄膜试件进行实验探索，结果表明：阻尼层可以有效提高结构的阻尼性能。ESHAGHI等[9]通过实验分析了磁流变液为芯层的环形圆板的动力学性能。

对夹层板的理论探索大多集中在矩形板[10-13]或各向同性材料圆板[14-15]。ZHAI等[16]结合哈密顿原理与纳维解求解了夹层板的动态特性，在验证效率和精度的基础上，得到了多参数对夹层板的影响规律。PILGUN、 AMABILI[17]研究了各向同性材料制成的复杂几何形状浅圆形圆柱板的非线性自由振动和受迫振动特性。WEI、QING[18]应用修正的耦合应力理论(Modified Couple Stress Theory，MCST)分析了圆形板轴对称静力弯曲、弹性屈曲和自由振动特性。JAVANI等[19]利用广义微分求积法对功能梯度圆板的振动问题进行了细致的研究。

综上可知，有关嵌入阻尼各向异性圆板结构的理论探索还处于空白阶段。本文作者在四边固支的边界条件下求解结构的理论模型，利用实验结果和有限元数值模拟结果验证理论模型的正确性；在此基础上进一步探索阻尼层比率、半径大小与阻尼层厚度比以及复合材料层与阻尼层厚度比对结构的影响，数值计算结果可为工程人员设计大刚度、高阻尼的复合材料结构提供一定的参考。

1 ECDCCPS固有频率和损耗因子的推导

嵌入式共固化复合材料阻尼圆板结构(Embedded Co-cured Damping Composite Circular Plates Structure，ECDCCPS)的几何结构如图1所示。为得到振动方程，做如下基本假设：(1)忽略不计ECDCCPS结构在厚度方向的变形；(2)每层界面之间不发生滑移。

1.1 结构的几何方程与本构关系

根据一阶剪切变形理论表述结构的位移场，各层位移函数用式(1)表示：

(1)

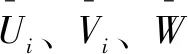
(2)

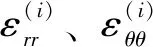
每层的应力-应变关系表示为

(3)

(4)

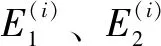
黏弹性层的损耗因子与复合材料层相比较大，因此对黏弹性层的弹性模量和剪切模量用式(5)表示：

(5)

1.2 控制微分方程的推导

由上面应力应变关系式可以得到ECDCCPS的应变能和动能为

(6)

(7)

式中：V表示ECDCCPS的体积；ρi表示第i层板的密度；S表示第i层r-θ方向中性面的面积。

黏弹性层的位移可以用上下面板位移来表示：

(8)

结构在四边固支边界条件为r=0处解有限及r=R处u=0，v=0，w=0，∂w/∂r=0，α=0，β=0。

考虑圆板关于坐标的周向对称性，采用分离变量法，设阵型解为

(9)

其中：ω*表示频率；非负整数m表示相应振型的周向波数，m=0表示轴对称振动。

Ritz法采用容许基函数来描述结构的位移，满足几何边界条件。位移函数用多项式函数乘以边界函数来描述，表示为

(10)

其中：ak、bk、ck、fk、lk为多项式函数的未知系数；k为整数；N表示位移幅度函数多项式的最高次数。

由拉格朗日能量函数得到结构的能量表达式为

Π=U-T

(11)

利用Rayleigh-Ritz法将拉格朗日能量函数相对于任意系数最小化得到阻尼复合材料圆板的自由振动方程为

(12)

将位移表达式代入控制方程并简化为矩阵形式

(K-(ω*)2M){X}=0

(13)

利用编程程序MATLAB计算式(13)的特征值，ECDCCPS结构的振动频率和损耗因子由式(14)计算可得：

(14)

2 算例分析与讨论

为了验证理论模型的有效性，采用模态应变能法计算四边固支边界条件下嵌入阻尼膜复合材料圆板结构的固有频率和损耗因子。其半径R=0.15 m，复合材料层的材料参数见表1，阻尼材料参数见表2。

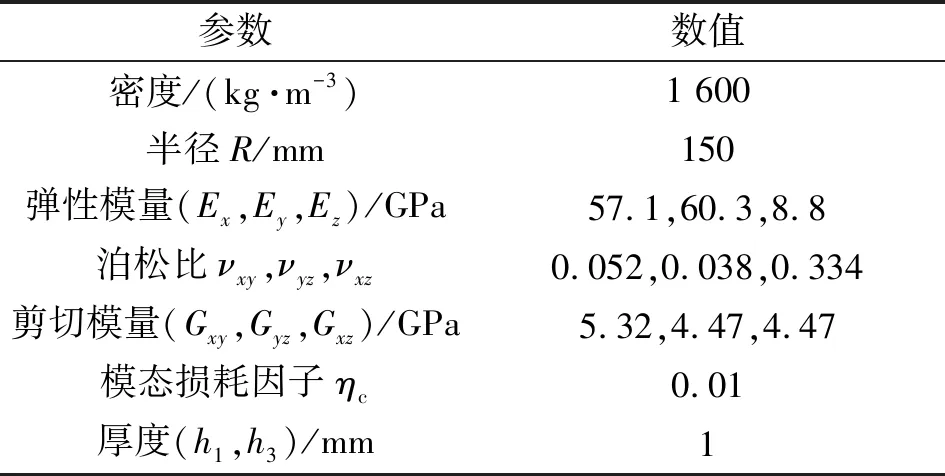
表1 ECDCCPS上下面板材料参数

表2 ECDCCPS阻尼层材料参数

此算例采用ANSYS有限元模拟对理论模型计算结果进行对比验证。板单元采用实体185单元，划分网格单元尺寸为1 mm，上、中、下3层共节点连接。图2所示为圆板划分网格，表3为Ritz法理论计算和有限元数值模拟计算结果对比。

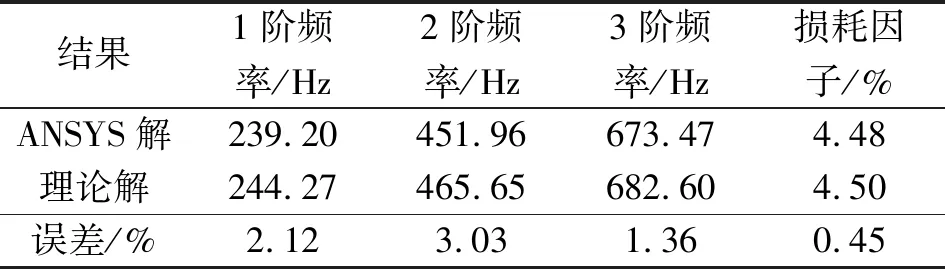
表3 理论与模拟结果对比

图2 圆板划分网格模型

如表3所示，Rayleigh-Ritz法计算的固有频率和损耗因子略微大于数值模拟结果，误差主要来源于理论模型的基本假定以及由于圆板形状的特殊性造成划分网格大小不一等因素，但前3阶固有频率和损耗因子误差均在5%以内，证明了理论模型的有效性。接下来将使用模态实验法对结果的正确性进行佐证。

3 实验平台的搭建与模型验证

3.1 试件的制备

采用碳纤维-环氧树脂预浸料加以双面刷涂工艺制作阻尼层，将复合材料和阻尼层在湿热环境箱中共固化得到ECDCCPS试件。圆板在固支夹具中放置如图3所示，夹持部分长度不计，实际测试半径为150 mm，上下面板总厚度为2.1 mm，阻尼层厚度为0.1 mm。圆板沿半径方向4等分，沿圆周方向18等分，测点共73个。

图3 圆板的固支夹具

3.2 实验测试系统组成及后处理

模态实验采用B &K公司的模态测试设备[8]，包括激励力锤(8206-002)、加速度传感器(4524-B-004)和PULSE (3560B)。具体实验装置如图4所示。

图4 实验设备

边界条件设定为四边固支，激励力锤设置在点38，如图5所示，测试采用单点激励多点响应，3次激励数值取平均，3次实验数据再次取平均，以获得准确的实验结果。具体测试过程如图6所示。

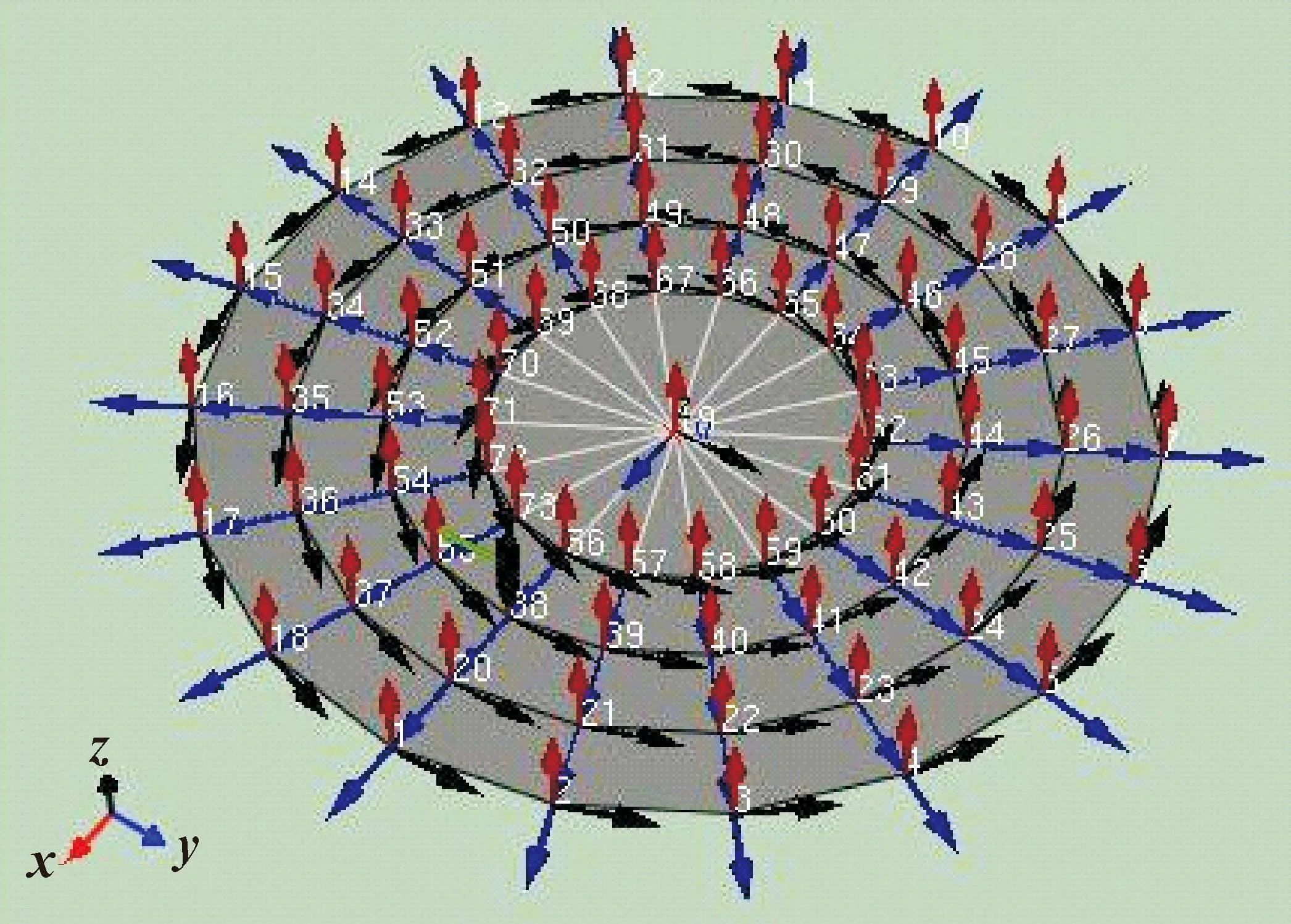
图5 激励力锤设置点

图6 实验测试过程

将实验结果导入后处理软件PULSE Reflex Version中进行参数识别设置，选择恰当的分析频带，模态参数分析方法采用有理多项式Z变换法，进行全局求解，迭代计算结果如图7所示。其中红色菱形表示模态频率、模态阻尼和模态振型都是稳定的，系统自动识别最佳的模态计算结果，表示为黑色圆圈，横坐标数值即表示实验得到的固有频率结果。

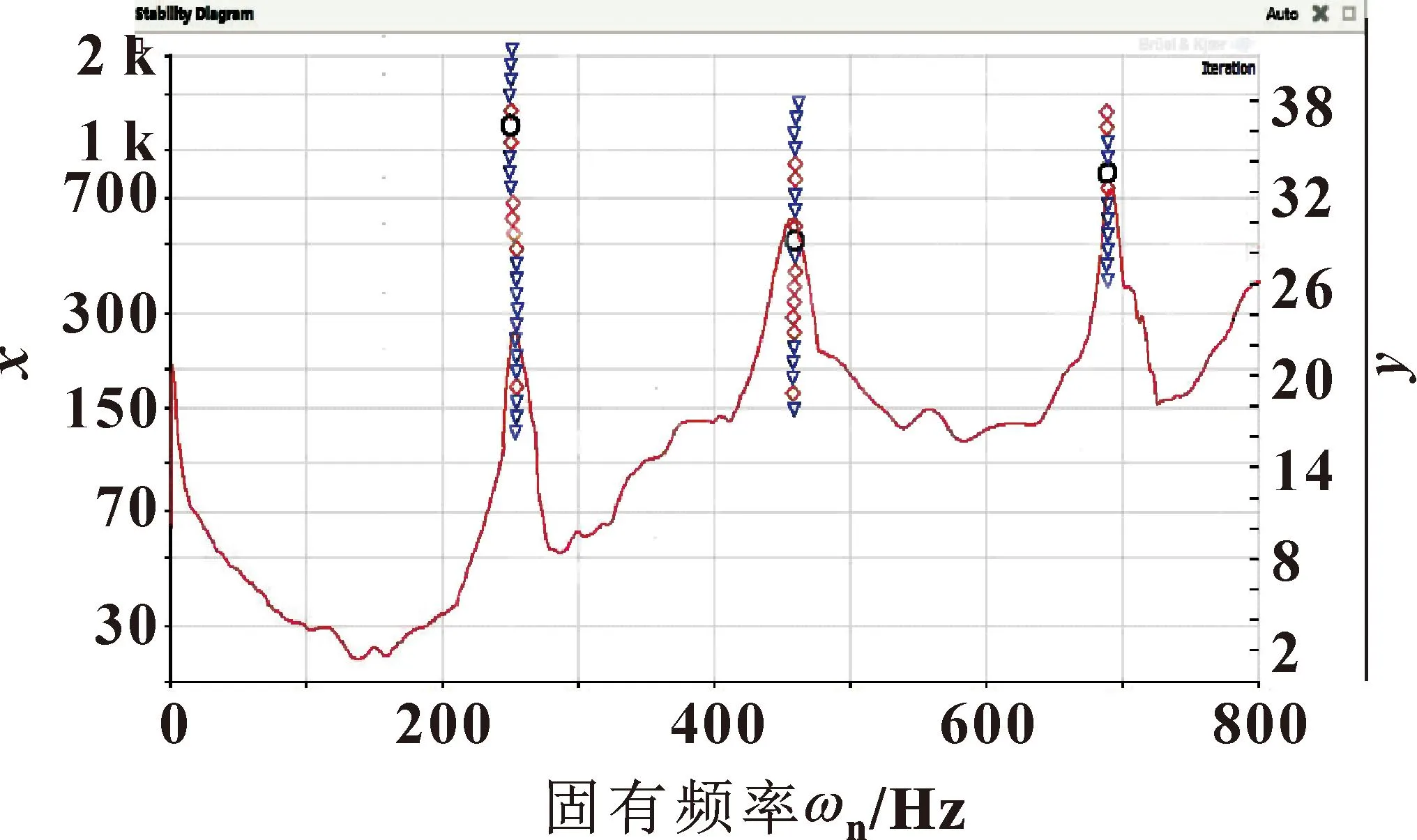
图7 迭代计算结果

3.3 实验结果及分析

表4为PULSE迭代计算得到的试件前3阶模态频率和模态阻尼。其中，误差1表示理论解与ANSYS模拟结果的相对误差，误差2表示实验结果与理论解的相对误差。

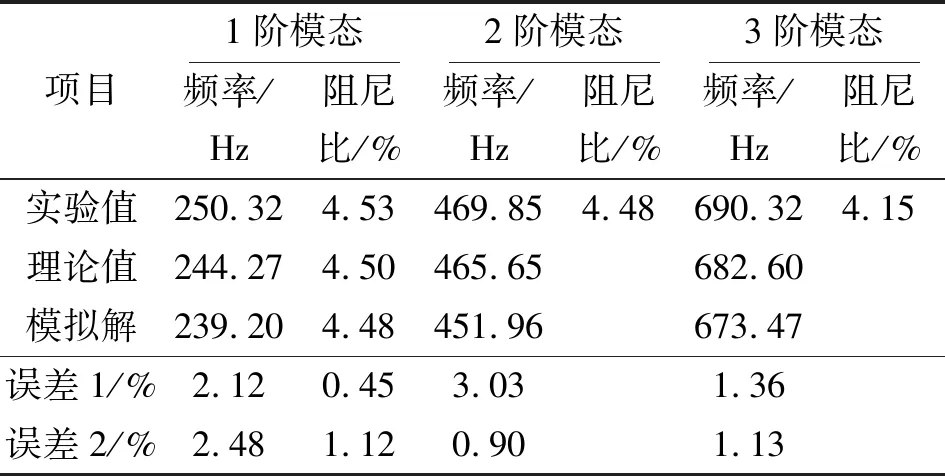
表4 理论、模拟与实验结果对比

由表4知：理论、实验和数值模拟结果误差均在5%以内，满足工程实际应用要求。模态实验进一步验证了理论模型的正确性，为工程实际应用Rayleigh-Ritz法求解ECDCCPS的固有频率和损耗因子提供便利，为固支边界条件下嵌入阻尼膜复合材料圆板结构的设计和优化奠定基础。

4 ECDCCPS的动态特性

在验证理论模型有效的基础上，运用该理论模型，进一步探讨阻尼层比率、半径大小与阻尼层厚度比以及上下面板厚度与阻尼层厚度比对自由振动频率和损耗因子的影响，得到四边固支ECDCCPS振动特性的变化规律。

4.1 阻尼层比率对结构振动特性的影响

将阻尼层比率定义为阻尼层厚度占板总厚度的比值。保持圆板厚度不变，改变阻尼层的厚度，图8所示固有频率和损耗因子随阻尼层比率的变化趋势。

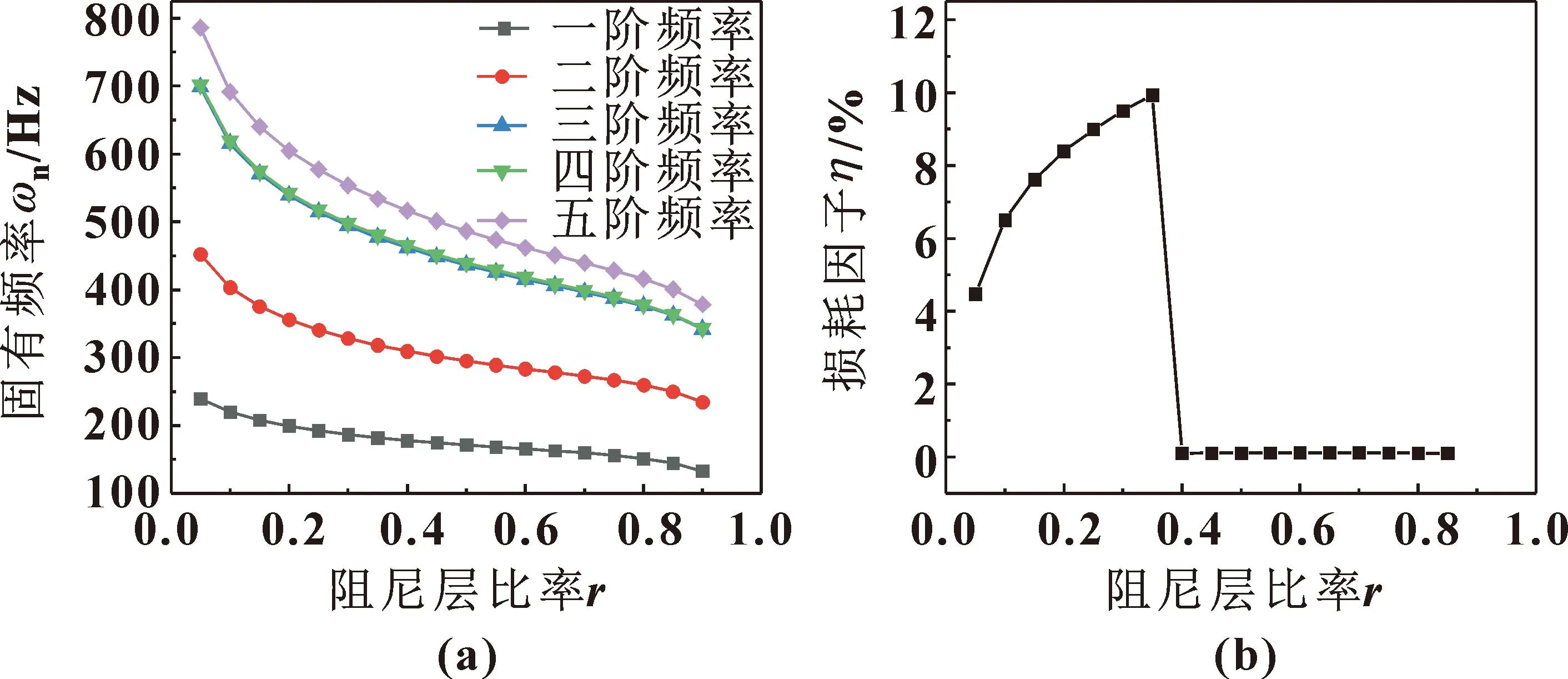
图8 阻尼层比率对ECDCCPS固有频率(a)和损耗因子(b)的影响

由图8可知：当结构的阻尼层比率增大时，结构的固有频率均呈现不断减小的趋势，高阶时表现更为显著；损耗因子则随阻尼层比率的增大先增大到峰值后急剧减小并趋于平缓，这说明存在结构设计的最优值，当阻尼层比率为0.4时，损耗因子达到峰值。这是因为当阻尼层厚度增加时，结构总厚度不变，而上下面板变薄，导致阻尼层的剪切应变不断减小。因此阻尼层越厚阻尼性能不一定越好，较薄的阻尼层更能明显增强结构的阻尼性能。

4.2 半径大小与阻尼层厚度之比对结构振动特性的影响

保持结构半径大小以及上下面板厚度不变，研究半径与阻尼层厚度比对ECDCCPS固有频率和损耗因子的影响。为表述方便，引入变量B，将其定义为半径值与阻尼层厚度之比。图9描述了改变B值时固有频率和损耗因子的变化规律。

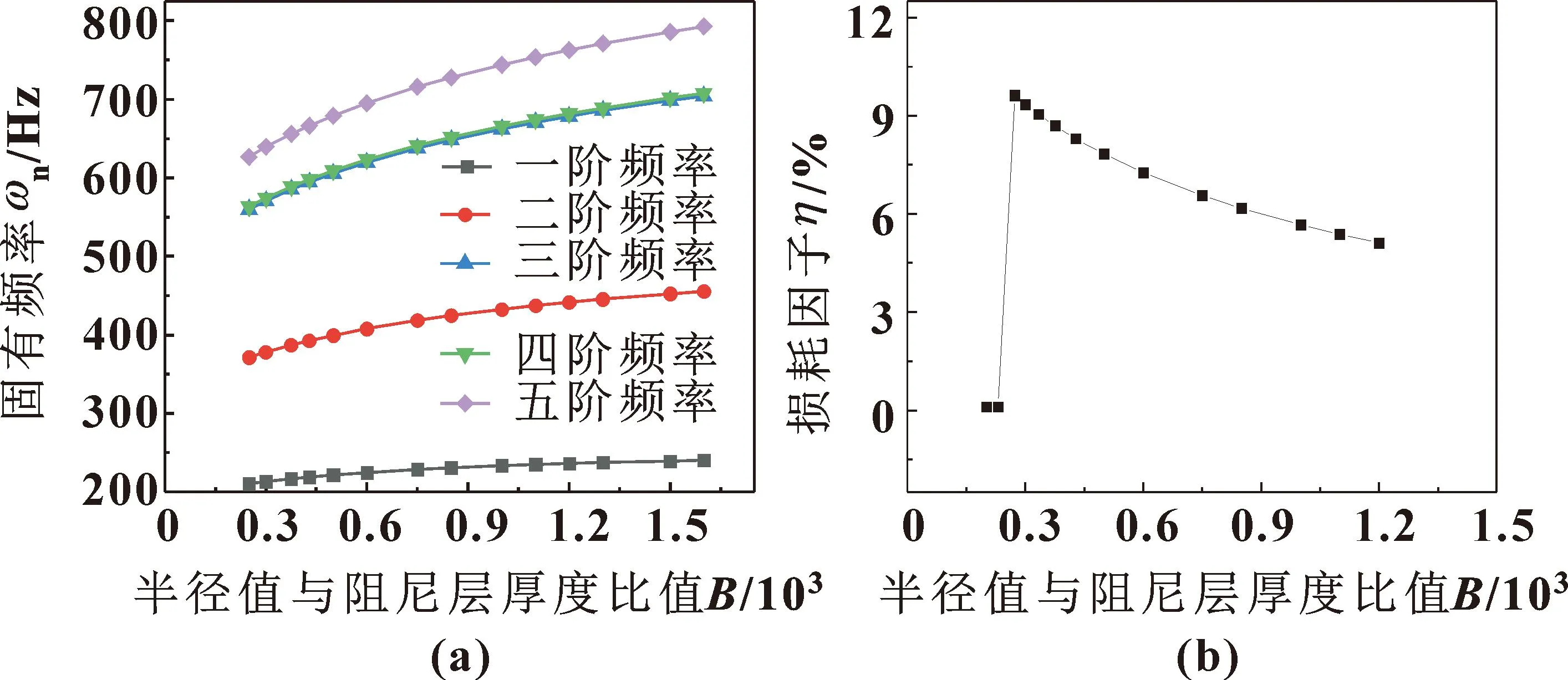
图9 B值对ECDCCPS固有频率(a)和损耗因子 (b)的影响

由图9可知：随着B值的不断增大，一阶固有频率不断增大并趋于平缓，高阶固有频率呈现不断增大的趋势；损耗因子随B值的增大有突变的情况，表现为先急剧增大到极大值后不断减小，说明该处存在结构设计的较优点。当B=273时，损耗因子达到峰值。这是因为此时恰当的阻尼层厚度使其得到了充分的受力变形，使得损耗因子达到最大。因此在半径一定的情况下，取与半径值适当比例的阻尼层厚度可以使结构拥有较大的刚度和较为理想的阻尼性能。

4.3 复合材料层厚度与阻尼层厚度之比对结构振动特性的影响

保持复合材料层厚度不变，改变阻尼层的厚度，定义二者比值为L，研究它对ECDCCPS动态特性的影响。图10描述了L随结构振动频率和损耗因子的变化规律。

图10 L值对ECDCCPS固有频率(a)和损耗因子(b)的影响

如图10所示：结构的固有频率变化趋势基本相同，随着L的增大而增大；损耗因子随L的增加先增大到极大值后不断减小。这说明在复合材料层厚度一定时，适当增加阻尼层厚度可以明显提高结构刚度，因此存在复合材料层与阻尼层厚度的较优比。当L=4时，结构的损耗因子较大，在此比例下的复合材料层和阻尼层使得ECDCCPS既有较强的刚度又有较为理想的阻尼性能，并且当结构的阻尼层厚度大于复合材料板厚度时，结构的刚度和阻尼性能均较差。

5 结论

文中研究了固支边界条件下ECDCCPS的自由振动特性。利用Rayleigh-Ritz法得到ECDCCPS的振动控制方程，求解了结构固有频率和损耗因子计算式；基于数值模拟与模态试验，验证了理论模型的正确性；并运用该理论模型进一步研究阻尼层厚度参数对ECDCCPS的影响规律，主要结论如下：

(1)当阻尼层比率为0.4时，损耗因子存在峰值。因此，较薄的阻尼层更能明显增强结构的阻尼性能；

(2)在半径一定的情况下，取与半径恰当比例的阻尼层厚度可以使结构拥有较大的刚度和较为理想的阻尼性能；

(3)存在复合材料层与阻尼层厚度的较优比，为ECDCCPS设计优化提供参考。