基于GWO-CMFH和改进ResNet轴承故障诊断

欧巧凤，彭泗田，李新民，熊邦书

(1.南昌航空大学图像处理与模式识别省重点实验室，江西南昌 330063；2.中国直升机设计研究所直升机旋翼动力重点实验室，江西景德镇 333001)

0 前言

滚动轴承广泛应用于各种旋转机械设备，是航空发动机等设备的核心组件之一[1]。滚动轴承是有寿件，由于疲劳或质量缺陷等因素产生局部损伤[2]，会使机械设备产生振动异常，甚至导致设备损毁和生产事故[3]。因此，对滚动轴承故障进行监测和诊断具有十分重要的意义。

目前国内外研究中，针对滚动轴承信号故障的诊断方法主要分为传统方法和基于神经网络的方法两大类。传统方法通过提取人工定义的信号特征进行故障分类识别，如2019年，CHEGINI等[4]提出一种基于经验小波变换的振动信号去噪和轴承故障识别方法，该方法分解信号时需要先验知识确定频带宽度；2020年，LI等[5]提出了基于包络峭度峰值自适应搜索变分模态分解模态数的方法，该方法中模态数搜索空间的确定基于现有先验知识；2021年，郑近德等[6]提出自适应自相关谱峭度的方法，以改进的经验小波变换为基础，对原始信号傅里叶谱进行包络与平滑处理后再分割。但在顺序统计滤波处理过程中，其窗口宽度需人工事先设定。 2021年，LI等[7]针对传统结构元素故障特征提取过程中容易出现脉冲信号遗漏的问题，提出了一种新的数学形态学滤波算子，用于获取更多的特征信息。在传统方法中，数学形态学滤波是一种非线性信号处理方法[8]，在机械故障诊断领域得到了广泛应用[9]。但该类方法在参数选择方面仍存在过度依赖专家先验知识的问题[10]。

而基于神经网络的方法不需要人工介入、可自动学习故障特征，已逐渐成为主流的故障诊断方法。如2021年，许子非等[11]提出多尺度卷积神经网络，用于复杂工况下端到端的轴承故障诊断，但该方法平均诊断精度不高；而自HE等[12]首次提出残差结构思想以来，残差网络(Residual Network，ResNet)被应用于解决传统卷积神经网络梯度爆炸和网络退化问题。如2021年，ZHANG等[13]提出一种在噪声标签下基于自适应损失加权元残差网络的方法，但该方法无法主动标记噪声标签；2021年，赵敬娇等[14]提出基于残差连接的一维卷积神经网络模型，对不同残差连接进行分析。但该方法诊断模型各参数的取值会不同程度影响诊断效果，模型鲁棒性欠佳。同时，针对输入特征在不同通道上相关性不同，且在不同空间位置的重要性不同的问题，上述方法都无法对关键故障特征信息进行针对性提取与学习。

据此，本文作者提出基于灰狼算法(Gray Wolf Optimization，GWO)结构元素自适应优化的组合形态高帽变换(Combination Morphological Filter-Hat transform，CMFH)，然后基于混合注意力机制改进的残差网络的轴承故障诊断方法。

1 方法

1.1 CMFH

设f(n)表示一维离散信号，其定义域n∈[0，1，…，N-1]，g(m)表示一维离散结构元素，其定义域m∈[0，1，…，M-1]，且N>M，则f(n)关于g(m)的开闭算子(Filter Opening Closing，FOC)和闭开算子(Filter Closing Opening，FCO)分别定义为

(1)

(2)

式中：。表示开运算；·则表示闭运算。则CMFH定义为

(3)

1.2 CMFH参数的GWO自适应优化

CMFH算子结构元素(Structural Element，SE)的形状和参数直接影响信号冲击特征提取性能[15]。但目前仍没有SE形状和参数的选取标准。考虑到SE越简单，进行形态学运算的时间复杂度越低。因此，文中采用一维直线型作为CMFH算子SE的形状。将SE长度作为优化目标，进行长度自适应最佳筛选。采用包络熵衡量提取信号中的冲击特征能力[16-17]，因此文中采用CMFH变换信号的包络熵作为优化的目标函数。假设给定信号为x(n)，则它的希尔伯特变换结果定义为

(4)

信号x(n)的包络a(n)为

(5)

包络a(n)归一化得到Pn，则EP为信号x(n)的包络熵值：

(6)

文中采用GWO[18]对CMFH结构元素长度值进行优化，自适应优化流程如图1所示。

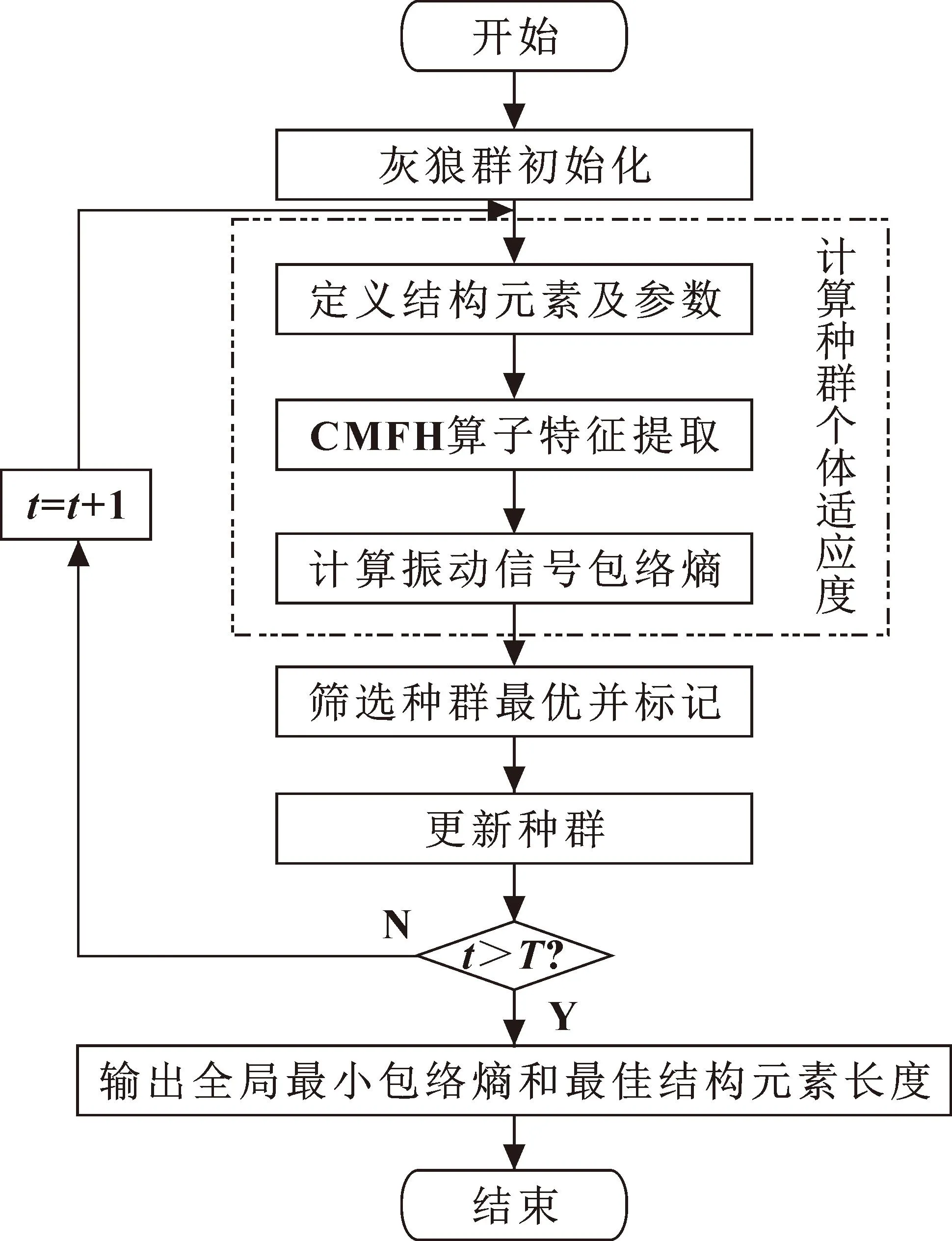
图1 基于GWO的CMFH参数自适应优化流程

步骤1，灰狼群初始化。在保证优化的结构元素长度准确性的前提下，为降低GWO算法的计算时间复杂度，设定迭代初始值t，最大迭代次数T，狼群规模S，待优化参数上边界U及下边界D，并以包络熵为目标函数。

步骤2，计算种群个体适应度。构造初始长度为L0的一维直线型CMFH算子结构元素，将灰狼群的最优位置对应CMFH算子结构元素的长度Li。通过CMFH算子提取轴承故障振动信号中的特征后，得到滤波后的振动信号，计算滤波后振动信号的包络熵值。则灰狼群第i个个体在第t次迭代的适应度为fi(t)。

步骤3，筛选种群最优并标记。选择包络熵值小的3个个体依次标记为α、β、δ，剩下的个体标记为ω。

步骤4，更新种群。根据α、β、δ的位置更新种群个体位置。

步骤5，当迭代次数t大于最大迭代次数T时，则停止更新种群，得到最优CMFH结构元素长度Ln；反之，返回步骤2继续执行循环。

1.3 二维时频图生成

轴承振动信号经GWO-CMFH滤波后，采用连续小波变换将该一维时域信号转换为二维时频图谱。

设一个基本小波为ψ(t)，且其定义域为：ψ(t)∈L2(R)。

(7)

式中：a、b均为常数，且a>0。

由式(7)可知，ψa,b(t)由ψ(t)先平移后伸缩变换得到，即当a、b的值不断变化时，得到函数ψa,b(t)。设x(t)为平方可积信号，且x(t)∈L2(R)，则其连续小波变换定义为

(8)

式中：x(t)为连续小波变换Wx(a，b)关于伸缩因子a和平移因子b的函数。其中，文中设定a为1 024，b为3，并采用cmor3-3小波基。小波变换后得到二维彩色时频图，为了减少后续神经网络的计算量，将时频图转换为灰度图，并采用直方图均衡方法增加其对比度，凸显故障特征。

1.4 基于混合注意力机制改进残差网络模型

文中提出通道域结合空间域的混合注意力机制改进ResNet。通道注意力模块通过分别采用全局最大值池化和全局平均池化学习不同通道间全局特征信息的相关性，最大值池化可提取图像的主要特征，平均池化可很好保留图像的背景信息，针对性地更新不同通道的注意力权重。而空间注意力模块则是通过学习不同空间位置特征信息的差异性，对重要位置特征针对性地加权。结合通道和空间2个维度提取故障特征，加强对关键特征信息的学习，弱化不敏感特征信息的关注度，从而进一步提高精度。设计网络如图2所示，模型参数如表1所示。

表1 混合注意力机制改进的残差网络参数

1.5 网络模型的训练与验证

文中轴承故障识别研究为多分类问题，损失函数采用交叉熵损失，其公式为

(9)

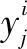
2 实验及结果分析

利用3种不同工况条件下轴承的振动信号数据集进行实验，针对小分类即不同程度的轴承故障进行诊断分析。数据集1为美国凯斯西储大学驱动端轴承SKF6205不同故障程度分类数据集，包括4大类和10小类数据：滚珠故障(刻伤尺寸0.177 8、0.355 6、0.533 4 mm)；内圈故障(刻伤尺寸0.177 8、0.355 6、0.533 4 mm)；外圈六点钟故障(刻伤尺寸0.177 8、0.355 6、0.533 4 mm)；正常。其中轴承采样频率为12 kHz，负载为0，转速为1 797 r/min。该数据集具有高转速的特点。

数据集2为东南大学公开轴承数据集，包括5类数据：滚珠故障、内圈故障、外圈故障、内圈和外圈故障、正常。其中轴承采样频率为2 kHz，负载为0，转速为1 200 r/min。该数据集具有中等转速的特点。

数据集3为作者团队在洛阳LYC轴承有限公司采集的直升机自动倾斜器滚动轴承数据集，包括4大类11小类数据：滚珠故障(刻伤尺寸1.0、1.3、1.5 mm，转速均为219 r/min)；内圈故障(刻伤尺寸1.0 mm、转速219 r/min，刻伤尺寸1.2 mm、转速219 r/min，刻伤尺寸1.2 mm、转速237.9 r/min，刻伤尺寸1.5 mm、转速219 r/min)；外圈故障(刻伤尺寸1.0、1.2、1.5 mm，转速均为219 r/min)；正常(转速均为219 r/min)。其中轴承采样频率为5 kHz，负载为0。该数据集具有低转速的特点。

验证文中方法的计算机硬件配置：Intel(R)Xeon(R)4114处理器、ROG STRIX-GTX1080Ti-显卡、SamsungDDR4-32GB内存、ATA SaDisk SD9TB8W1-2TB。

文中实验验证共分为3部分：数据预处理、模型训练、模型测试。其中，数据预处理包括划分数据集和数据增强2个步骤。首先，将收集到的数据集按照7∶3的比例划分为训练集和测试集；然后，分别将不同故障程度类别数据集经过GWO-CMFH滤波，再经过连续小波变换、直方图均衡化得到数据增强后的时频特征图，并将该时频特征图作为模型的输入用于故障诊断。待训练集训练完毕后，保存模型权重，将测试集送入训练好的模型中进行测试，并得到最后实验结果。详细实验流程如图3所示。

图3 实验流程

如图3所示，文中实验在数据预处理阶段，一维轴承振动信号先经过自适应CMFH形态学滤波运算，抑制背景噪声并增强故障特征；然后经过小波变换转成二维时频特征图，并采用直方图均衡化进行数据增强。在模型训练中，提出基于注意力机制改进的残差网络进行训练；最后，进行模型验证并采用精度和混淆矩阵等作为轴承故障诊断模型的评判指标。

2.1 CMFH最优结构元素长度L自适应确定

根据图1所示流程设定迭代初始值t=1，最大迭代次数T=50，狼群规模s=30，待优化参数上边界U=10，下边界D=1，SE长度迭代初始值L0=10。文中以西储大学12 kHz驱动端内圈0负载、转速为1 797 r/min、0.177 8 mm刻伤故障信号为例，得到包络熵和结构元素随迭代次数变化曲线如图4所示。可知：当迭代至第2次后，包络熵值处于稳定状态，最小值为8.118，且对应最优结构元素长度为3。

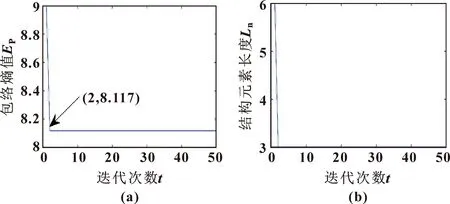
图4 包络熵(a)与结构元素长度(b)随迭代次数的变化曲线

因此取最优长度3为CMFH结构元素长度，并在该内圈故障信号中加入5%高斯白噪声进行滤波实验，结果如图5所示。

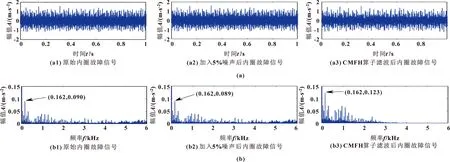
图5 CMFH算子滤波前后时域波形(a)及包络谱(b)

由滚动轴承的结构参数可计算得到该内圈的故障频率为162 Hz。如图5所示，原始信号的包络谱故障频率幅值为0.090 m/s2，经过CMFH算子滤波后内圈信号的包络谱故障频率幅值为0.123 m/s2，高于加5%高斯白噪声的包络谱故障频率幅值0.089 m/s2。可知：基于GWO优化后的CMFH算子对故障信号具有滤除噪声能力，且增强故障冲击特征。

为验证GWO-CMFH自适应最优SE长度对不同强度噪声的抗噪性能，并防止添加噪声过大造成故障特征被淹没的问题，向西储大学内圈0.177 8 mm刻伤故障原始信号中分别添加1%、3%、5%、7%、9%的高斯白噪声，以及不添加高斯白噪声，进行最优SE长度在不同噪声环境下对比实验。实验结果如表2所示，表中包络熵与信噪比均为滤波后信号的参数指标。

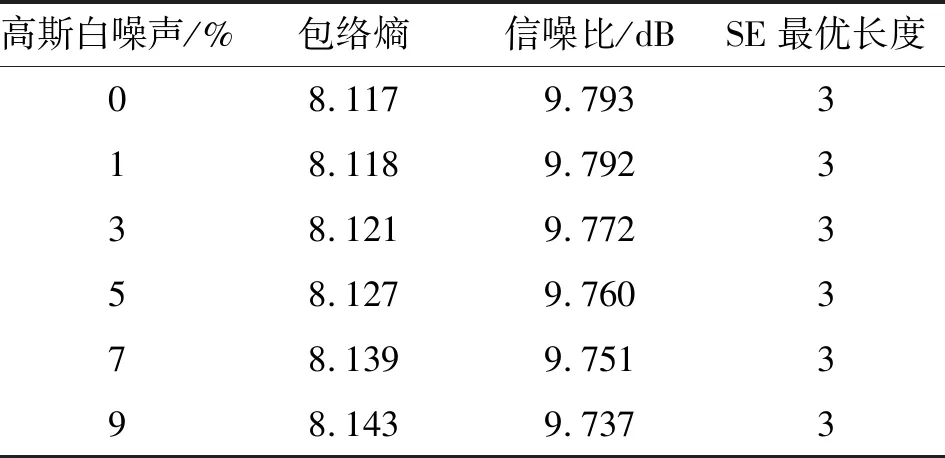
表2 CMFH滤波后的信号指标及SE最优长度

由表2可知：GWO-CMFH算子在不同强度噪声干扰下，其自适应SE最优长度不受影响，具有很好的抗噪能力和鲁棒性。

为了验证自适应SE长度是否最优，自定义SE长度在2～8内以1为间隔，以12 000个信号数据作为计算批次尺寸。多次计算无噪声情况下，不同SE长度CMFH滤波后，西储大学0.177 8 mm刻伤尺寸的3种故障类型信号包络熵，实验结果如表3所示。

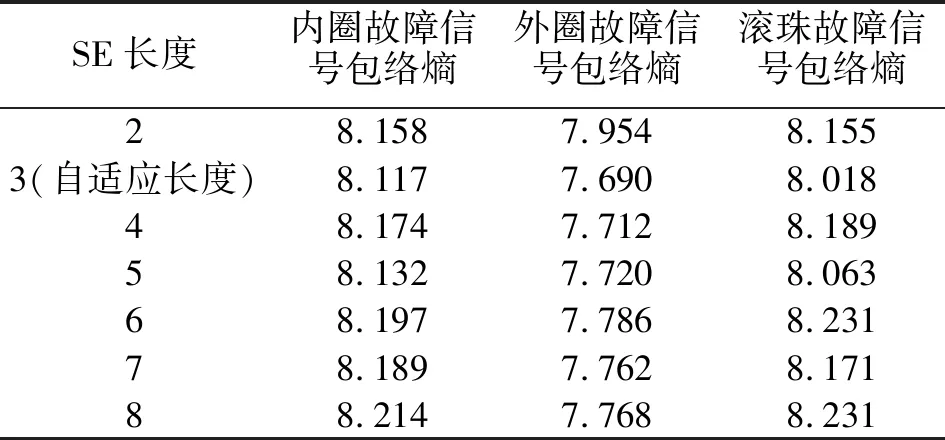
表3 不同SE长度下CMFH滤波后信号的包络熵

由表3可知：西储大学3种故障类型信号中，SE自适应长度下的CMFH算子滤波后信号的包络熵值均为最小即故障特征增强效果最好，且与图4(b)中SE长度优化结果一致。证实SE自适应长度下CMFH算子滤波、凸显故障特征效果最优，且具有很好的稳定性，可进一步提高故障诊断的效率。

针对不同数据集信号，使用GWO算法对CMFH算子最优SE长度自适应选取。3个公开数据集结果最优SE长度如表4所示。

表4 不同数据集最优SE长度

2.2 基于混合注意力机制改进的残差网络故障诊断对比实验

数据集1共生成二维时频图12 100张，数据集2共生成二维时频图8 000张，数据集3共生成二维时频图8 600张。将每个数据集分别按70%、30%的比例划分为训练集、验证集用于模型训练与实验验证。为验证CMFH滤波的有效性，对数据集信号添加高斯白噪声进行对比实验。经多次实验发现：添加噪声过大时，容易造成信号故障特征的泯灭，失去实验的可靠性。故向数据中添加1%的高斯白噪声进行实验验证。对信号不同数据预处理后进行多次对比实验，其中改进残差网络诊断精度结果如表5所示。

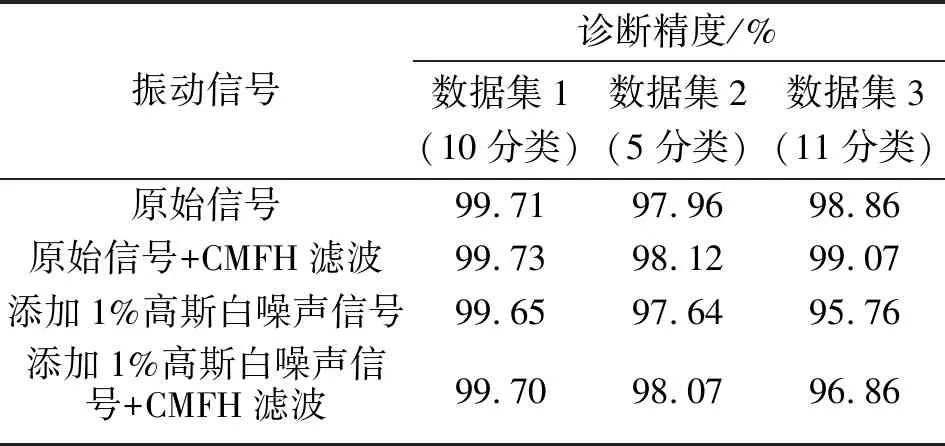
表5 振动信号滤波前后改进ResNet的诊断精度

由表5可知：原始信号在CMFH滤波后的诊断精度均高于滤波前，添加1%的高斯白噪声信号在CMFH滤波后的诊断精度也高于滤波前，证明CMFH滤波有效。

经过多次实验验证，将模型准确率作为评价指标，实验结果如图6所示。数据集1的10分类准确率为99.73%，数据集2的5分类准确率为98.12%，以及数据集3的11分类准确率为99.07%。证明文中方法对不同故障程度条件下滚动轴承故障诊断有效。

为验证文中方法的优越性，与赵敬娇等[14]提出的残差连接和1D-CNN的方法以及余志锋等[19]提出的基于VMD-CWT和改进CNN的方法进行对比实验，结果如表6所示。针对不同程度的小分类轴承故障，基于t-SNE对文中方法、文献[14,19]方法提取的不同故障程度数据集特征进行可视化对比展示，如图7所示。

表6 文中方法与文献[14,19]的故障诊断精度对比

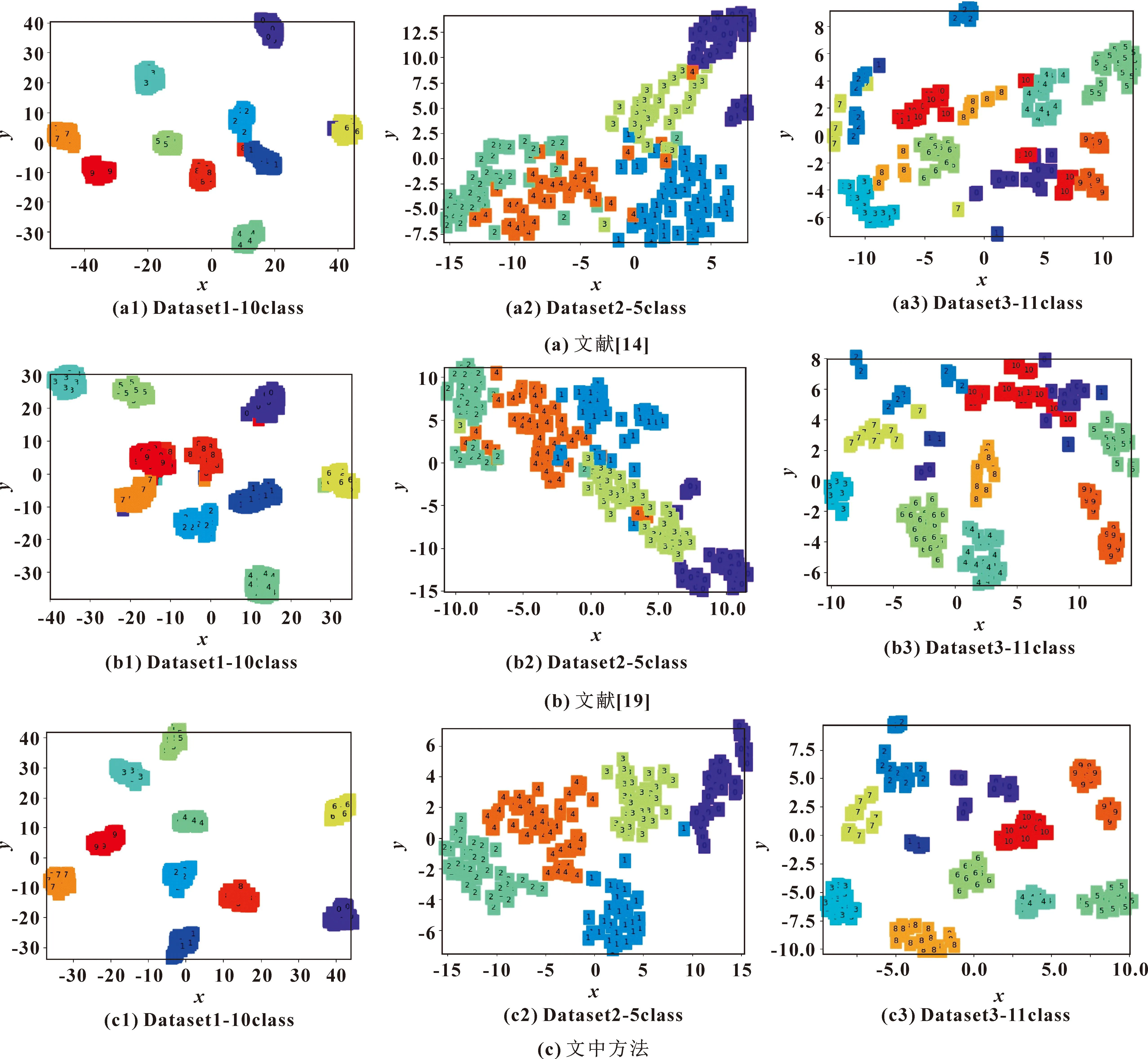
图7 不同故障程度数据集特征可视化对比

由表6可知：文中方法在5种不同故障程度数据集上均高于文献[14]以及文献[19]的识别精度。

从图7中基于t-SNE的特征提取可视化效果对比可知，文中方法在不同工况条件下，对于小分类的不同故障程度轴承数据集提取特征的能力均强于文献[14,19]，可更好地区分开不同程度的小分类故障，从而更有效解决不同小分类故障程度的轴承故障诊断。

3 结论

文中针对不同工况条件下、不同离散程度小分类轴承故障现有诊断方法准确率不高的问题，提出基于GWO-CMFH和改进的ResNet轴承故障诊断方法。首先，GWO算法对CMFH滤波算子SE长度进行自适应最优筛选，基于最优SE长度的CMFH算子对轴承信号进行滤波运算，增强故障特征；然后，基于连续小波变换将滤波后的振动信号转换成时频特征图谱，并进行直方图均衡化增强特征；最后，基于混合注意力机制改进的残差网络对时频特征图谱进行故障诊断。

因此，针对不同故障程度小分类轴承故障诊断精度不高的问题，文中方法实验结果表明：

(1)GWO-CMFH方法有效解决CMFH算子参数依赖专家先验知识选取的问题，可自适应选择最优参数，具有很好的稳定性。自适应CMFH滤波算子在不同强度噪声干扰下具有很好的抗噪性和鲁棒性，可增强不同程度小分类数据故障特征的提取能力。

(2)基于混合注意力机制改进的残差网络，融合了空间注意力机制和通道注意力机制，对通道域和空间域多维度故障特征针对性地提取和训练。在西储大学(10分类)、东南大学(5分类)以及文中(11分类)不同故障程度的小分类数据集上分别得到99.73%、98.12%和99.07%的诊断精度，此模型具有很好的泛化性能。且较文献[14,19]方法的诊断精度明显提高，可提高不同程度轴承故障诊断的精度。

但文中自适应CMFH形态学滤波需通过优化算法实现，效率不高。下一步的重点是研究将CMFH形态学滤波嵌入网络模型，并实现自适应训练优化，提高轴承故障诊断效率。