机械载荷作用下梯度多孔材料圆板非线性力学行为的研究
孙昊栋马连生王娅娟陈思阳
(1.河西学院,张掖 734000;2.兰州理工大学,兰州 730050)
梯度多孔材料因其在厚度方向上孔隙率的变化,致使其材料性能也沿厚度方向连续变化。这种材料性质使得梯度多孔材料结构具有许多优异的力学性能。Magnucka-Blandzi[1]研究了边缘简支的圆形多孔板在径向均布压缩和均布载荷(压力)作用下的力学特性。Jabbari等[2]研究了压电层对板屈曲载荷、压电层-多孔板厚度比以及孔隙率变化的影响,并基于Sanders非线性应变-位移关系,将计算结果与均匀的、非线性、对称分布的圆形板进行了比较。Khorshidvand[4]研究了均匀径向载荷作用下多孔材料圆板的屈曲力学行为,并分析了多孔板厚度比、孔隙率等对结果的影响。Feyzi和Khorshidvand[5]研究了多孔材料性质对多孔圆板过屈曲行为的影响。Mojahedin等[6]基于经典版理论,研究了多孔材料固体圆板的热稳定性和力学稳定性。基于高阶剪切变形板理论,文献[7]研究了多孔材料固体圆板在径向载荷作用下的屈曲问题。孙昊栋[8]研究了梯度多孔材料性质、边界条件以及载荷等因素对结构单元力学性能的影响。
1 基本方程
假设圆柱坐标系(r,φ,z)的原点在圆板的圆心,rφ平面置于圆板未变形时的几何中面,z轴垂直于圆板的几何中面。梯度多孔材料圆板半径为b,厚度为h。圆板承受均布径向载荷p和横向面内载荷q。
设梯度多孔材料的孔隙率沿厚度方向按以下两种模型的方程变化[9]。

根据Zhang和Zhou[10]引入的物理中面概念,梯度多孔材料圆板的物理中面为:

运用能量法推导出梯度多孔材料圆板的控制方程以及边界条件,并退化到经典板理论下的控制方程及边界条件,用打靶法求解无量刚控制方程,得到了径向载荷与面内横向载荷共同作用时圆板非线性力学行为的数值解。
无量纲控制方程及边界条件为:

2 数值结果与分析
图1给出了对称材料模型下圆板在横向载荷与径向载荷共同作用时,中心挠度随横向载荷变化的曲线。图1中实线表示e0=0(各向同性材料)时的弯曲路径,虚线表示e0=0.5时的结果。可以得出,当径向载荷为定值时,圆板中心挠度随横向载荷的增大而增大。孔隙率越大,中心挠度增长越快,与曲线的变化趋势一致。此外,边界条件对结果也有显著影响。
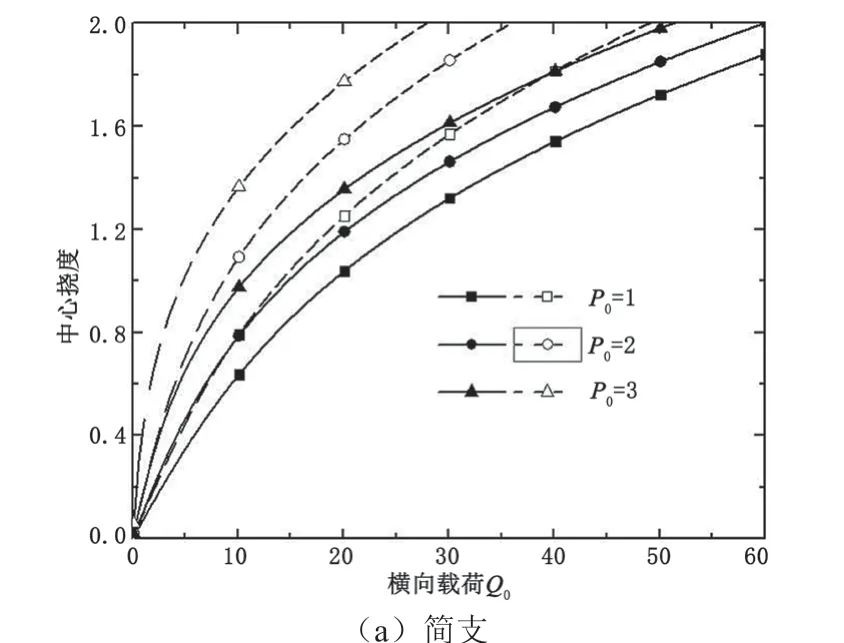
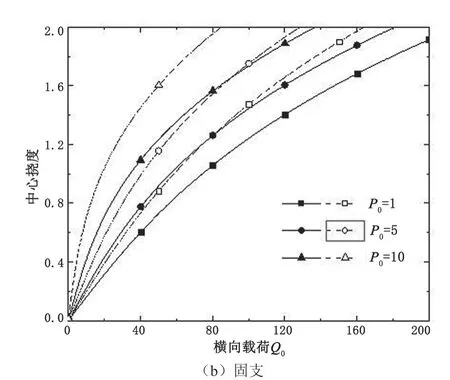
图1 圆板中心挠度随横向载荷的变化曲线(对称材料模型)
图2给出了非对称材料模型下,圆板在横向载荷与径向载荷共同作用时中心挠度随横向载荷变化曲线。可以看出,非对称材料模型下,圆板的稳定性更低。它的变化趋势与对称材料模型下的结果是相同的。
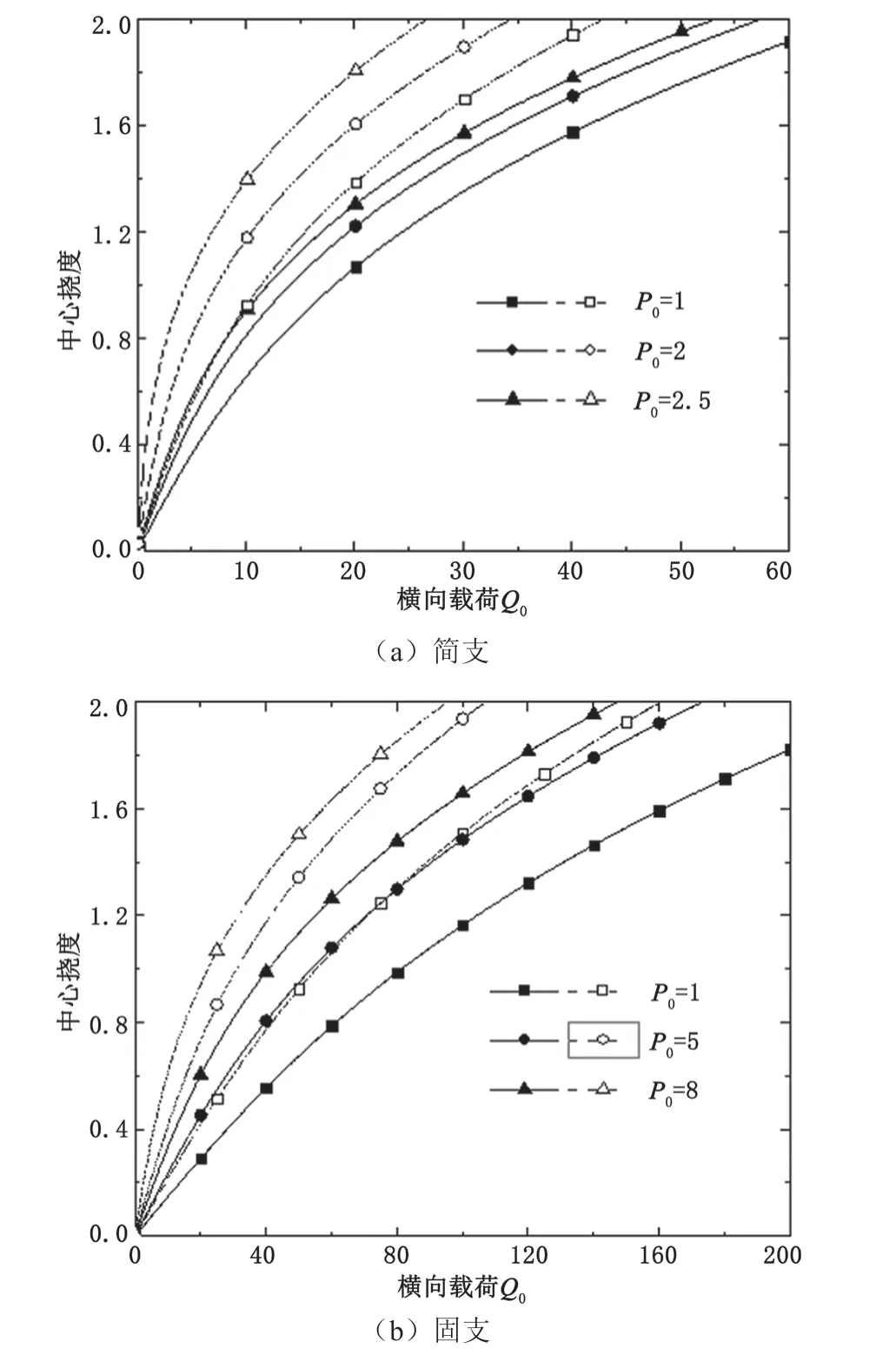
图2 圆板中心挠度随横向载荷的变化曲线(非对称材料模型)
图3给出了对称材料模型下,圆板在横向载荷与径向载荷共同作用时中心挠度随径向载荷变化的曲线。同样的,图3中实线表示e0=0(各向同性材料)时的结果,虚线表示e0=0.5时的结果。从图3可以看出:当横向载荷为零时,圆板发生过屈曲变形;横向载荷不为零时,圆板发生弯曲变形;在径向载荷作用之始,圆板已经发生弯曲变形。
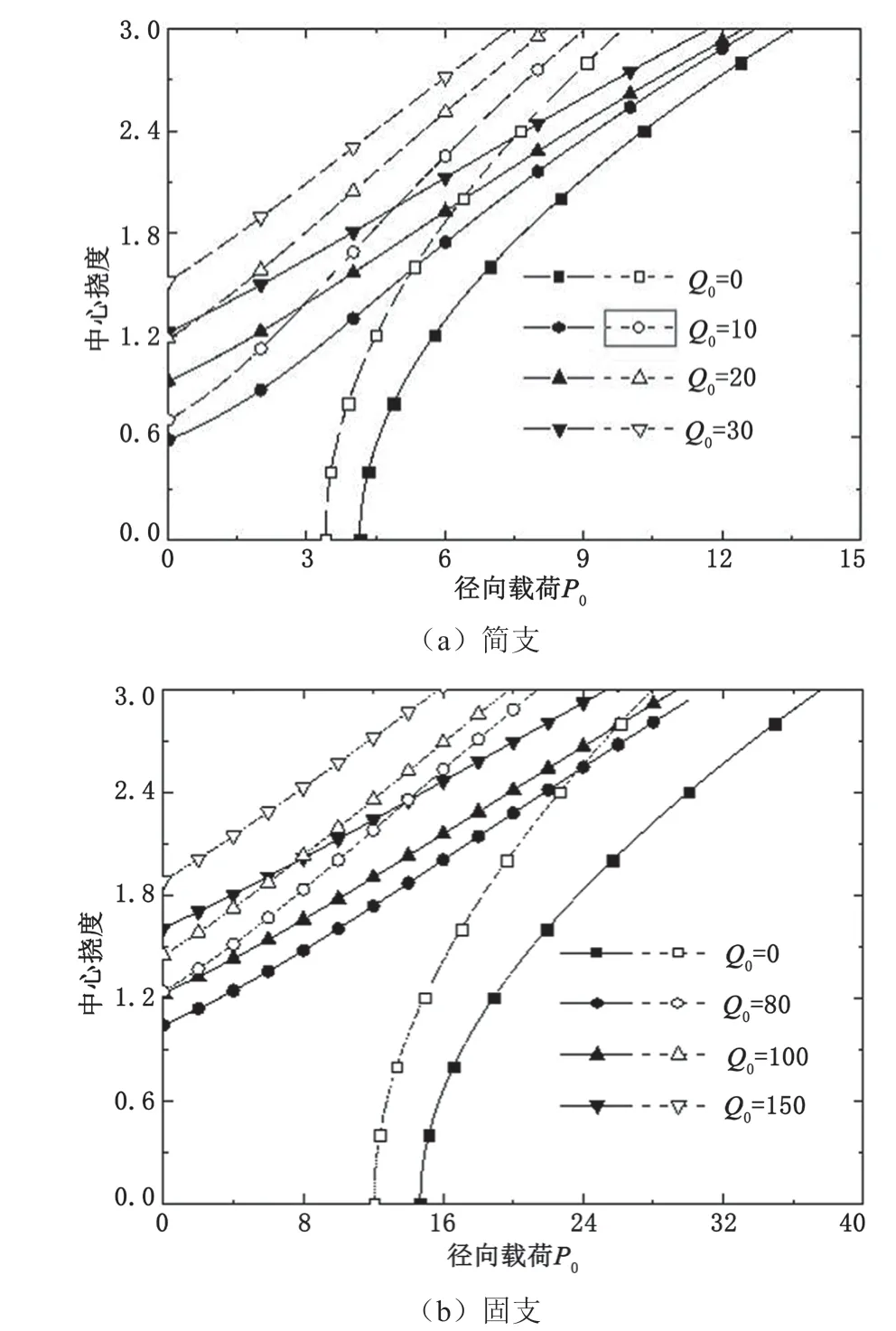
图3 圆板中心挠度随纵向载荷的变化曲线(对称材料模型)
图4给出了非对称材料模型下,梯度多孔材料圆板在横向载荷与径向载荷共同作用时中心挠度随径向载荷变化的曲线。圆板中心挠度的变化趋势与对称材料模型下的结果一致,但是圆板的稳定性相对较低。
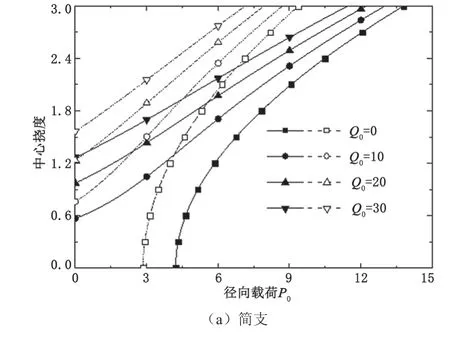
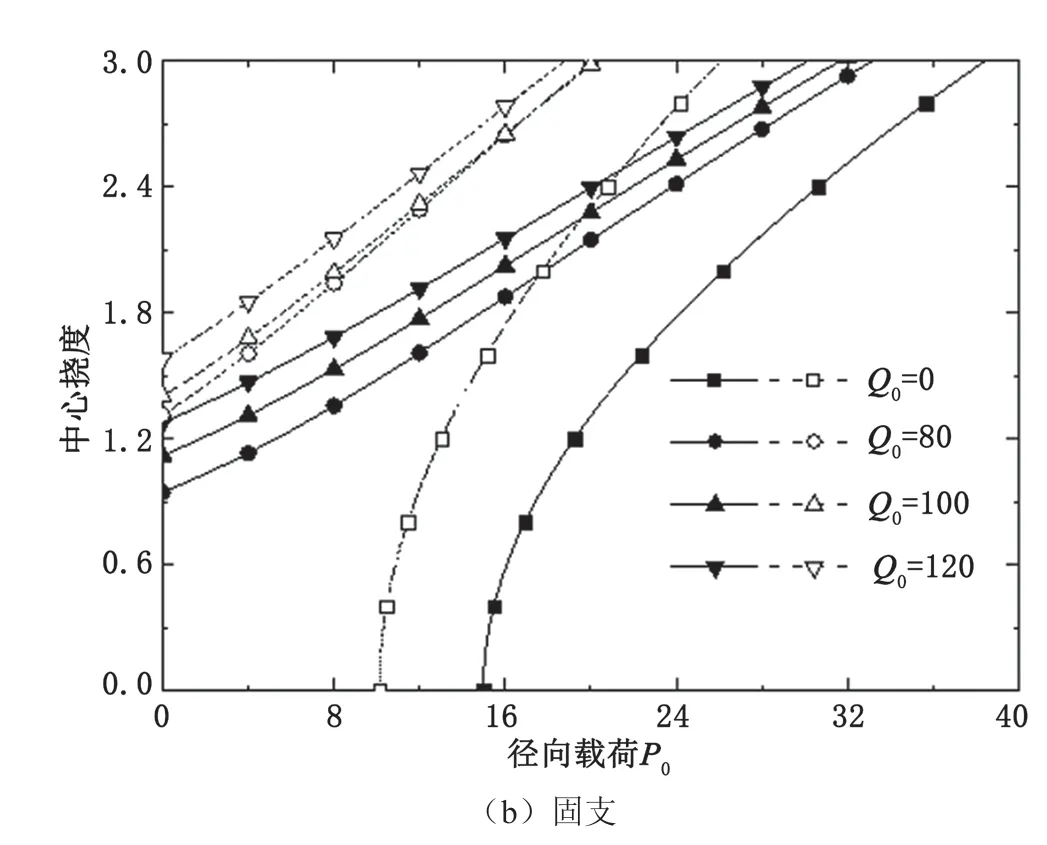
图4 圆板中心挠度随纵向载荷的变化曲线(非对称材料模型)
3 结论
(1)孔隙率对圆板的稳定性有显著影响。当径向载荷为定值时,圆板的中心挠度随着横向载荷的增大而增大。相对于非对称材料模型,对称材料模型下圆板的有效刚度大,稳定性高。
(2)边界条件对圆板的稳定性有重要影响。当横向载荷为零时,圆板发生过屈曲变形;横向载荷不为零时,圆板发生弯曲变形;在径向载荷作用之始,圆板已经发生弯曲变形。

