轴对称变厚度圆板反对称弯曲的传递矩阵法

周欣竹，郑建军，范兴朗，张 炜，叶 浩

(1.浙江工业大学 土木工程学院，浙江 杭州 310023；2.浙江省工程结构与防灾减灾技术研究重点实验室，浙江 杭州 310023)

在土木、水利和机械工程中，各种材料和各种形状的板结构得到广泛的应用[1-4]。变厚度圆板的应用也不罕见，如汽轮机叶盘、板式离合器、往复机械中的活塞和电视塔基础等[5-7]。由于变厚度圆板弯曲方程过于复杂，一般解析解仅限于简单荷载作用下的线性变厚度板[5]。对于复杂荷载作用下的一般变厚度圆板，大多采用数值方法。刘叶丹等[8]提出了变厚度圆板弯曲的初参数法，这种方法对板结构优化设计具有一定的优越性。李欣业等[9]提出了线性变厚度圆板的有限差分法。周欣竹等[10]基于特殊函数理论给出了Winkler地基上环板单元的传递矩阵，并用于一般变厚度环板的静力分析。吴敏达等[11]考虑板的剪切变形，应用摄动法给出了指数变厚度圆板和环板的级数解。近年来，Vivio等[12]获得了一类幂型变厚度圆板弯曲的解析解。这些研究都限于变厚度圆板或环板的轴对称弯曲，而对于反对称弯曲文献中鲜有报道[5-7]。而在实际工程中，如果变厚度圆板垂直置于液体中，液体对圆板的压力可以分解为轴对称荷载和反对称荷载。因此，研究轴对称变厚度圆板的反对称弯曲对于进一步理解板的受力特性具有理论意义，而且对于圆板设计和厚度优化也具有参考价值。

1 基本方程和等厚度圆环板弯曲的解析解

考虑如图1所示的变厚度圆板，周边简支或固支，将圆板划分成N的单元，其中：第1个是圆板单元，其余N-1个是环板单元。圆板承受反对称荷载为

P(r,θ)=p(r)cosθ

(1)

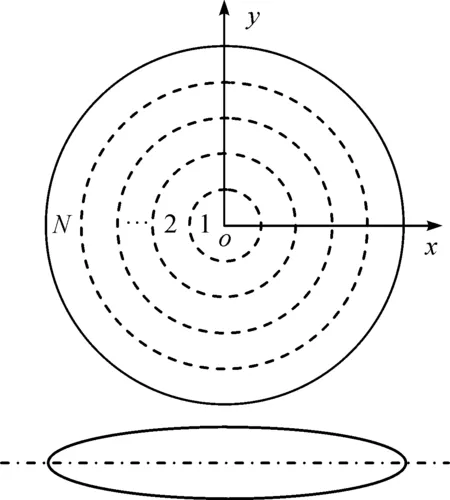
图1 轴对称变厚度圆板及其单元划分

为了分析这些板单元，将它们按等厚度处理，很显然，单元数N越大，这些板单元的组合越接近原来的轴对称变厚度圆板。设第i个板单元的弯曲刚度为Di，所承受的荷载为

Pi(r,θ)=pi(r)cosθ

(2)

根据板壳理论，第i个板单元的挠度Wi(r,θ)满足如下方程：

(3)

根据外荷载的形式，设挠度Wi(r,θ)为

Wi(r,θ)=wi(r)cosθ

(4)

相应的径向转角Φr(r,θ)、径向弯矩Mr(r,θ)和径向剪力Vr(r,θ)分别为

Φir(r,θ)=φir(r)cosθ

(5)

Mir(r,θ)=mir(r)cosθ

(6)

Vir(r,θ)=vir(r)cosθ

(7)

式中：φir(r)，mir(r)，vir(r)分别表示为

(8)

(9)

(10)

式中μ为板材料的泊松比。

将式(4)代入式(3)并消去cosθ有

(11)

式(11)的解由两部分组成：一部分是与式(11)相对应齐次方程的解，另一部分是式(11)的特解。很显然，相应于式(11)的齐次方程解为

(12)

式中：ci(i=1,2,3,4)为待定系数；函数fi(r)(i=1,2,3,4)分别为

(13)

(14)

(15)

(16)

根据常微分方程理论，式(11)的特解可设为

(17)

式中：d1(r)，d2(r)，d3(r)，d4(r)分别为r的函数，满足下列条件：

(18)

(19)

(20)

将式(17)代入式(11)并注意式(18～20)有

(21)

联立求解方程式(18～21)可得

(22)

设第i个环板单元的内半径和外半径分别为ri-1和ri，则d1(r)，d2(r)，d3(r)，d4(r)分别为

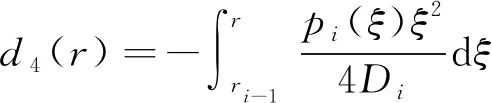
(23)

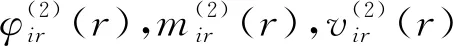
(24)

(25)

(26)

这样，就得到等厚度环板反对称弯曲挠度、径向转角、径向弯矩和径向剪力的解析解。对于等厚度圆板单元，由于板中心的挠度和弯矩有限，只需令c3=c4=0就可以得到挠度、径向转角、径向弯矩和径向剪力。

2 环板单元传递矩阵和变厚度圆板总体传递矩阵

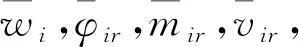
(27)

Ci=[c1,c2,c3,c4,1]T

(28)

对于第i个环板单元，当r=ri-1时，由式(12，14～17，24～26)有

Ai-1Ci=Qi-1

(29)

式中Ai-1为

(30)

求解方程组式(29)可得

(31)

(32)

同样，当r=ri时，由式(12，14～17，24～26)可得

Qi=BiCi

(33)

式中Bi为

(34)

由式(31，33)可得

Qi=TiQi-1

(35)

式中环板单元的传递矩阵Ti为

(36)

对于圆板单元，c3=c4=0。当r=r1时，由式(12，14～17，24～26)可得Q1为

(37)

式中B1为

(38)

根据传递矩阵法原理，对于图1所示的变厚度圆板有

(39)

式中总体传递矩阵T为

(40)

无论是周边简支还是固支，利用两个边界条件求得系数c1和c2，将c1和c2代入式(37)求出Q1，再利用传递关系式(35)求得各节圆上的挠度、径向转角、径向弯矩和径向剪力。

3 数值验证和讨论

考虑一轴对称变厚度圆板，半径为a，弹性模量为E，泊松比μ=0.3，板厚变化方程h(r)=h0[1-r/(2a)]，所承受的荷载P(r,θ)=p0(r/a)cosθ，板周边简支和固支两种情况，挠度W(r,θ)和轴向弯矩Mr(r,θ)分别写成

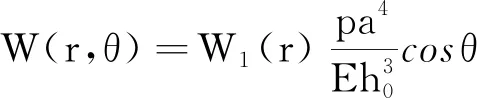
(41)

Mr(r,θ)=M1(r)pa2cosθ

(42)

计算发现：当将圆板划分成100 个等厚度单元时，结果收敛令人满意。令N=100，W1(r)和M1(r)的计算结果如图2～5所示，其中TMM和FEM分别表示传递矩阵法和有限单元法。从图2～5可以看出：传递矩阵法与有限元法吻合良好，对于简支圆板，W1(r)和M1(r)的最大相对误差分别为0.068 5%和0.379%，对于固支圆板，W1(r)和M1(r)的最大相对误差分别为1.09%和0.856%。因此，传递矩阵法的有效性得到数值验证。

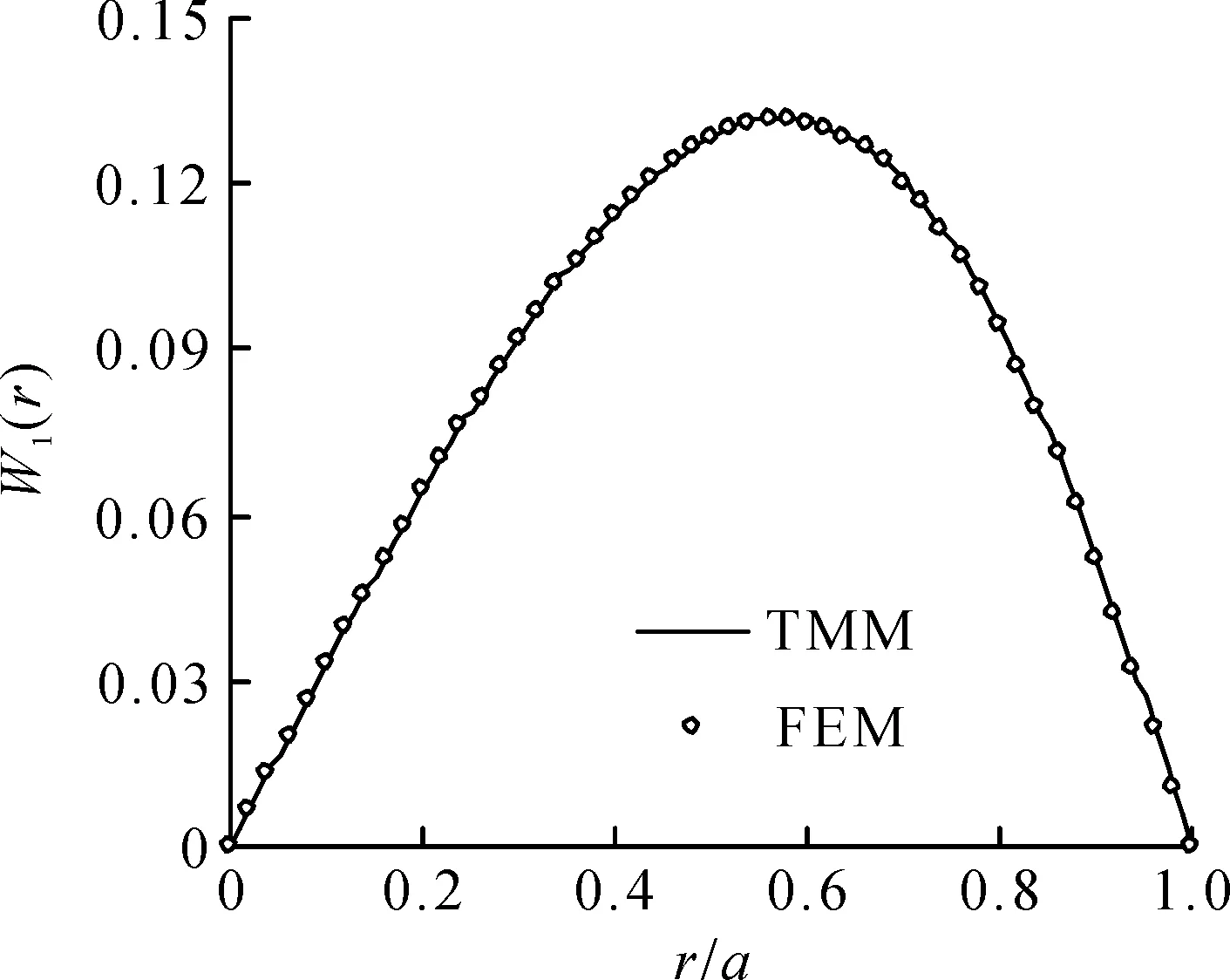
图2 简支圆板挠度

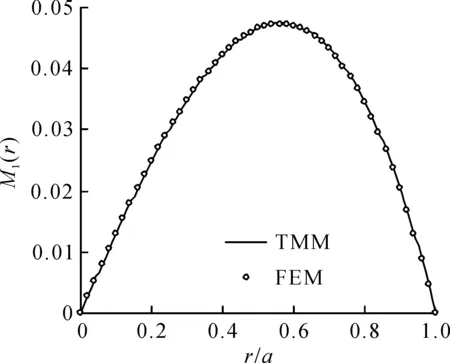
图3 简支圆板径向弯矩

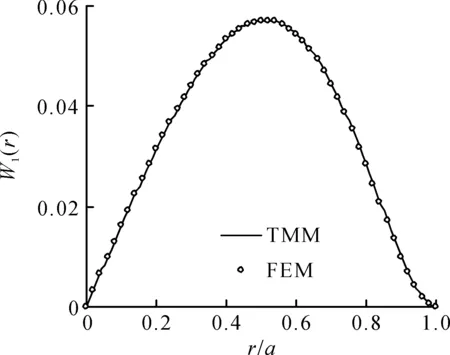
图4 固支圆板挠度

图5 固支圆板径向弯矩

下面讨论板厚变化对挠度和径向弯矩的影响。设半径为a，弹性模量为E，泊松比μ=0.3，板厚变化方程h(r)=h0exp(αr)，承受的荷载P(r,θ)=p0(r/a)cosθ，令W1(r)和M1(r)的最大值分别为W1max和M1max，对于周边固支圆板，产生负的径向弯矩，如图5所示，令M1(r)的最小值为M1min，计算结果如图6～10所示。从图6～10可以看出：板厚参数变化对板挠度影响较大，而对板径向弯矩影响较小。当α从-0.5增大到0.5时，简支板最大挠度和最大径向弯矩分别减小83.8%和17.8%，固支板最大挠度和最大径向弯矩分别减小85.8%和37.4%，而固支板的最小径向弯矩增大32.4%。

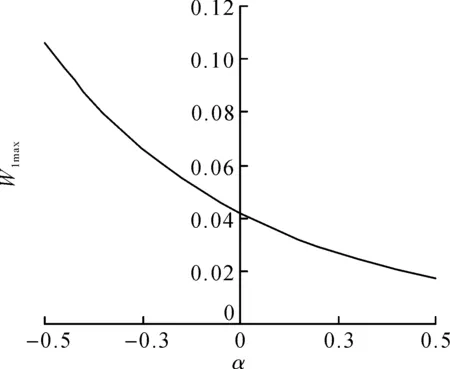
图6 简支圆板最大挠度

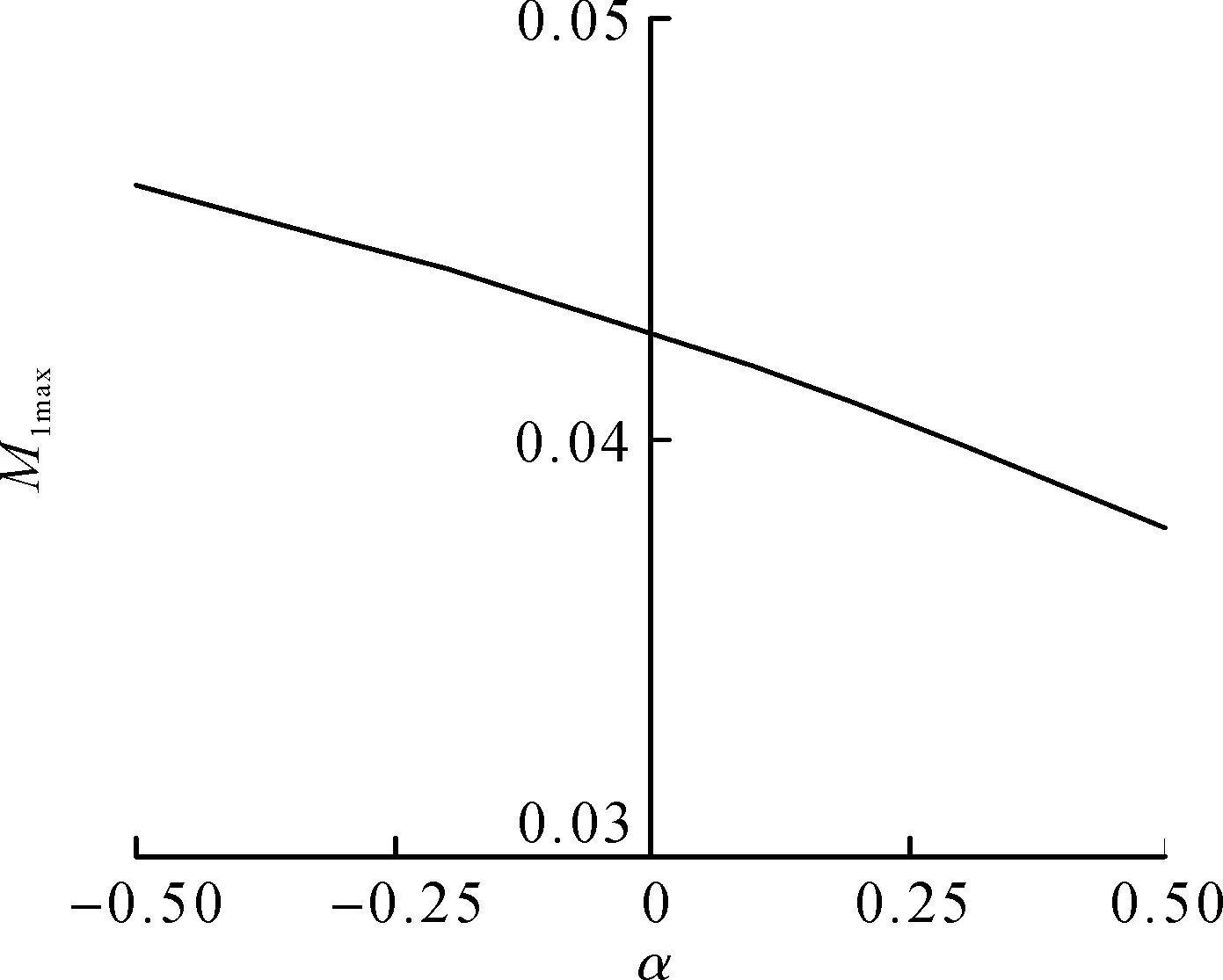
图7 简支圆板最大径向弯矩

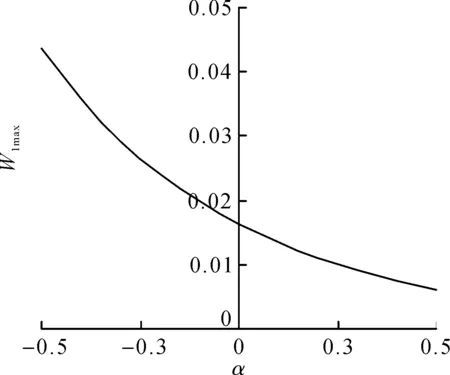
图8 固支圆板最大挠度

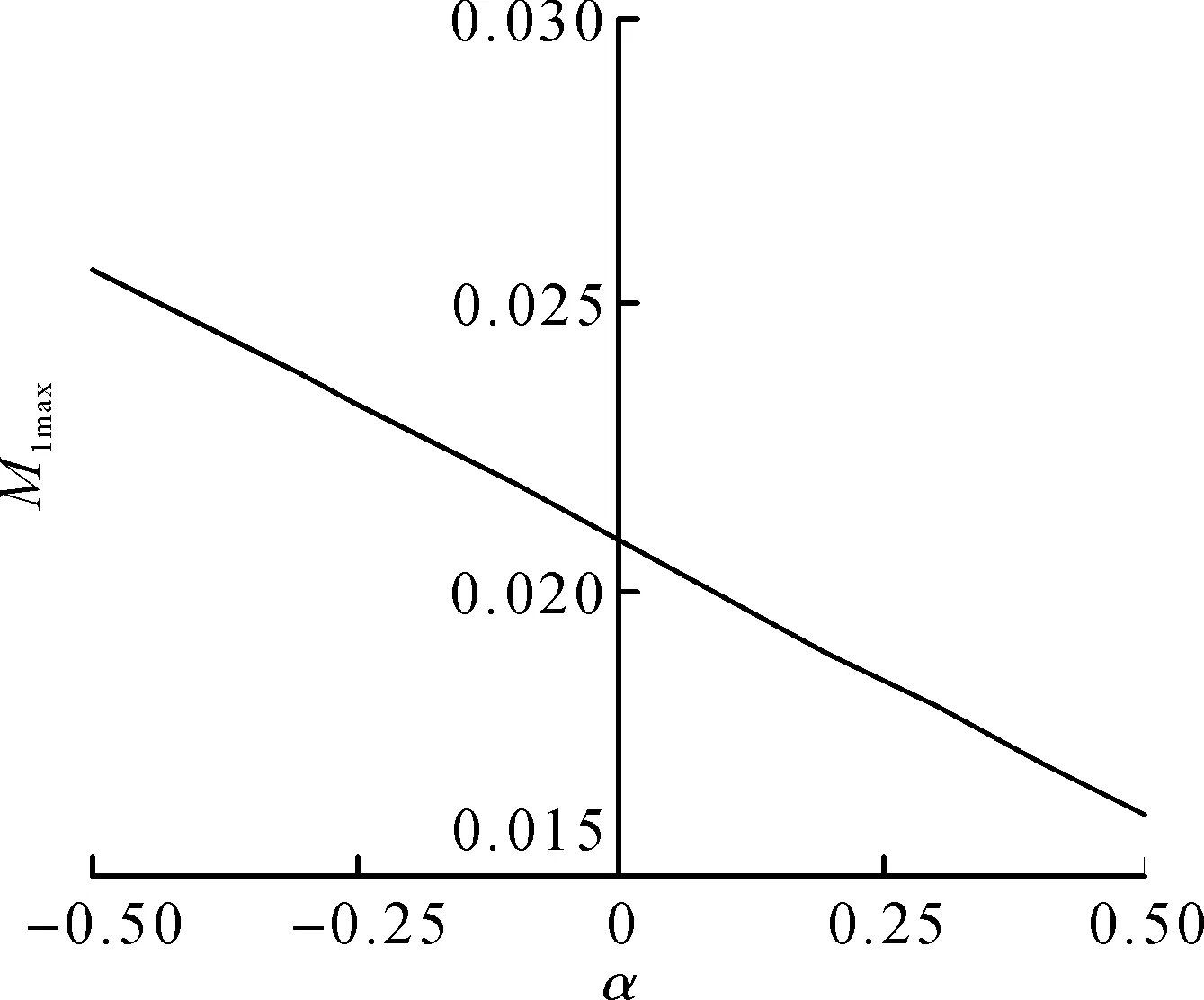
图9 固支圆板最大径向弯矩

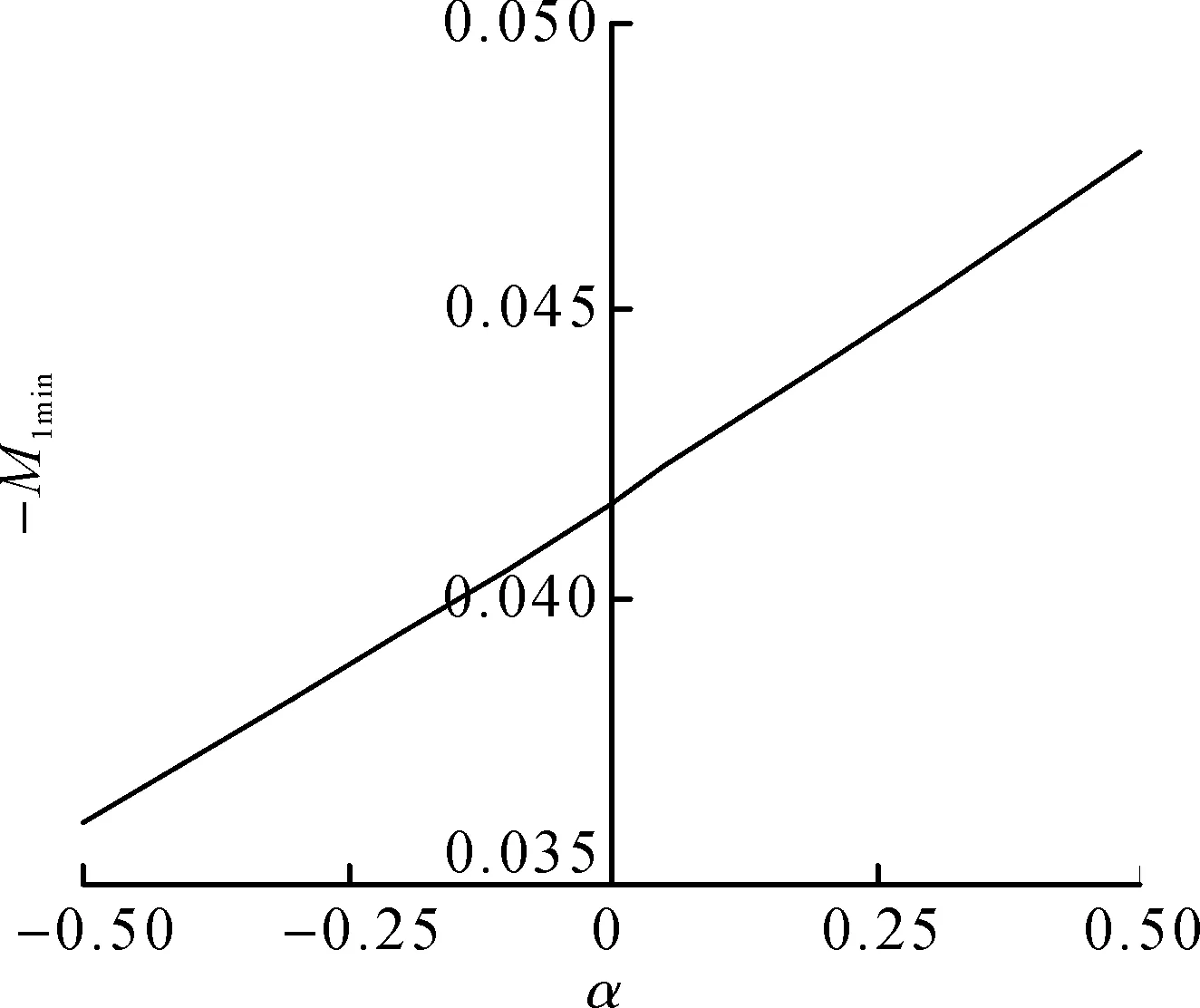
图10 固支圆板最小径向弯矩

3 结 论

基于等厚度环板反对称弯曲挠度、径向转角、径向弯矩和径向剪力的解析解，导出了环板单元的传递矩阵，提出了轴对称变厚度圆板反对称弯曲的传递矩阵法。该方法的主要优点：可以通过增加单元数模拟复杂变厚度板，提高计算精度，而总体传递矩阵的阶数始终保持5 阶，节省计算机内存。与有限单元法比较，证实了该传递矩阵法的有效性，讨论了板厚度变化对圆板最大挠度、最大径向弯矩和最小径向弯矩的影响。

本文得到了浙江工业大学研究生核心课程项目(GZ17571060001)和本科核心课程建设项目(PX-48181685)的资助。