真空-堆载联合预压法处理吹填土地基的大变形有限元分析

沙 玲，刘 鸿，王国才

(1.浙江建设职业技术学院 建工系，浙江 杭州 311231；2.浙江工业大学 岩土工程研究所，浙江 杭州 310023)

真空-堆载联合预压法是在真空和堆载预压法的基础上发展起来的一种软弱地基处理方法，具有造价低，施工工期短和工后沉降小等优点，该方法在大面积软土地基处理上虽然得到了广泛应用，但是在预压机理、施工工艺方面的理论研究同工程实践相比相对滞后，有一些理论、设计与施工问题仍未能得到圆满解决，如加固深度、沉降计算方法、地基处理效果和对周边环境影响等。因此，国内外许多学者和工程技术人员对此进行了深入研究，如赵维炳等[1]建立了砂墙地基平面应变和轴对称情况下的等效公式，提出了数值分析中砂井地基的处理技术；李豪等[2]根据固结度等效的原则，提出了一种简化的真空-堆载联合预压法数值模拟方法；袁静静等[3]对Abaqus软件进行二次开发，实现了真空-堆载联合预压法处理软基的数值计算；Leong等[4]通过实验的方法分析了超载预压和真空预压在土体强度增长方面的差异；吴跃东等[5]和何长明等[6]根据现场监测资料和原位与室内测试资料，分析了真空-堆载联合预压法的加固效果；郑晓国等[7]结合数值计算研究了真空预压影响区土体的变形机理，分析了联合堆载、隔离墙两种防治措施的效果；杨俊杰等[8]通过室内模型实验研究了真空灌浆法水泥浆的流动机理；Yan等[9]、王柏欢等[10]、彭劼等[11]以及张力等[12]分别对真空-堆载联合预压处理后的地基土沉降、水平位移、孔隙水压力分布规律、固结度、土体强度增长和含水量等方面进行了研究，分析了控制软基工后沉降的方法；韩培锋等[13]研究了循环冲击荷载下跑道软土的沉降及孔压变化。这些研究成果从不同角度揭示了软土地基处理的工程特性和加固效果，丰富了现有地基处理相关理论，并用于指导工程实践。

为进一步了解真空-堆载联合预压法的加固机理和地基处理效果，笔者采用Abaqus有限元软件对真空-堆载联合预压作用下的吹填土地基进行数值模拟与计算，分别采用大变形和小变形固结理论计算预压处理后吹填土的沉降、水平位移和超静孔隙水压力，并与实测结果进行对比分析，探讨联合预压处理过程中吹填土地基的变形和超静孔隙水压力分布规律。

1 工程概况

台州湾循环经济产业集聚区是浙江省“十二五”期间重点规划建设的14 个产业集聚区之一，总面积约562 km2。台州东部新区是该集聚区的核心区，区内地貌单元属滨海平原，拟建场地多为原始滩涂和吹填土组成。场区内3～5 m范围内为吹填土，吹填土下伏20～40 m的深厚淤泥质黏土和黏性土。区内的吹填土和淤泥质黏土有“三高一低”的特点，即高含水量、高孔隙比、高灵敏度和低强度，工程性质较差，需要经过处理后才能被开发利用。区内土层的基本物理力学性质指标如表1所示。

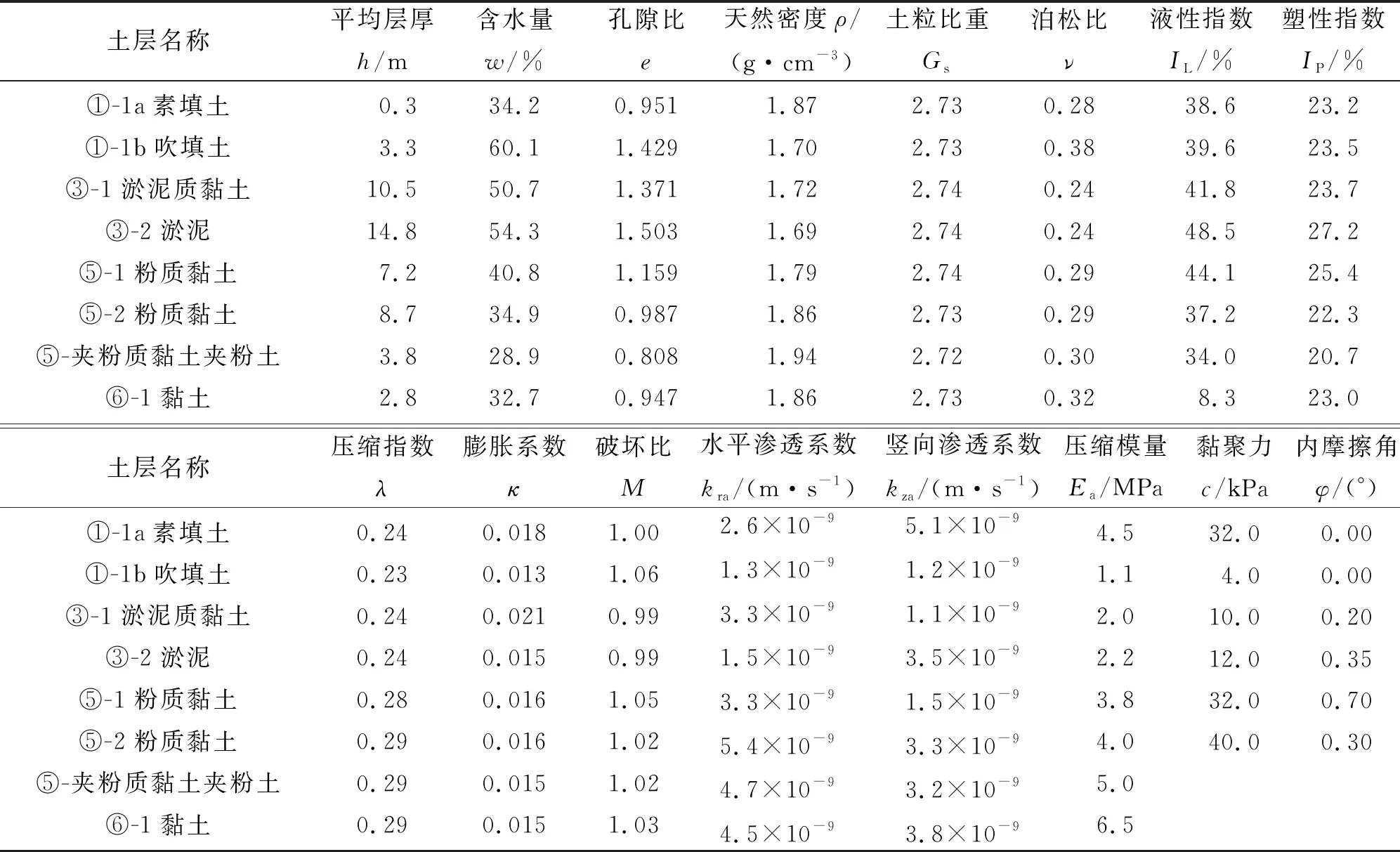
表1 地基土的主要物理力学性质指标

根据常见软土地基处理方案的优缺点并考虑东部新区的建设周期以及工程投资等因素，台州东部新区道路区主干道采用两次预压法即真空预压和真空-堆载联合预压法进行处理，地基处理深度约20 m，预压时间225 d(第一次真空预压45 d，第二次真空预压180 d)；而道路区次干道和地块区则采用无砂垫层真空预压法进行处理，处理深度分别约12，6 m，预压时间分别为150，120 d。台州东部新区工程场地鸟瞰图如图1所示。

图1 工程场地鸟瞰图

2 计算模型的建立

2.1 材料模型

在数值模拟计算时，上覆堆土采用线弹性模型模拟；下伏吹填土和软土考虑到真空与堆载联合预压过程中的剪胀或剪缩以及非线性力学行为，采用修正剑桥模型[14-15]，其屈服条件为

(1)

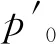
(2)

式中φ′为土的有效内摩擦角。

2.2 砂井地基的简化处理

在砂井地基固结沉降计算时，可将砂井或塑料排水板地基转换成砂墙地基，将三维问题转换成二维平面应变问题进行分析[1]。转换后的砂墙地基水平渗透系数kxp和竖向渗透系数kzp分别是实际砂井地基渗透系数的Dx和Dz倍，即

kxp=Dxkra

(3)

kzp=Dzkza

(4)

式中：kra，kza分别为砂井地基的水平和竖向实际渗透系数；Dx，Dz分别为水平和竖向渗透系数调整系数，计算式分别为

(5)

(6)

2.3 塑料排水板等效直径的确定

塑料排水板的等效直径dw是指与砂井地基固结效果相同的等效排水板直径，其计算公式为

(7)

式中：b，分别为塑料排水板的宽度和厚度；α为换算系数，一般取值0.75～1.0。

塑料排水板通常采用正方形或等边三角形进行布置。此时，单井的有效排水区直径de可按照面积等效的原则确定。当塑料排水板以正方形布置时，de=1.128sd；以正三角形布置时，de=1.05sd，其中sd为塑料排水板的间距。

2.4 有限元模型的建立

考虑到问题的对称性，塑料排水板、地基土和地面堆土采用平面应变模型。模型加固区宽度取35 m。根据试算，发现加固区范围以外70 m、排水板底15 m处的位移，应力和孔压非常小。因此，取计算模型宽度105 m、深度35 m。模型底部设为不透水边界，且X和Y方向为固定约束；左、右边界均为不透水边界，X方向固定、Y方向自由；模型表面为完全自由边界。

在网格划分时，考虑到大变形理论与小变形理论对固结沉降计算结果的影响，需要选取不同的有限元单元。对于小变形情况，地面堆土采用8节点孔隙流体/应力二次积分单元CPE8R，地基土体则采用专门用于流固耦合的8节点孔隙流体/应力缩减积分单元CPE8RP；对于大变形情况，则分别采用CPE4和CPE4P单元。为了提高计算精度和计算速度，地基加固区域网格划分较密，较远处则逐渐稀疏。模型及网格划分情况如图2所示。

图2 真空-堆载联合预压法计算模型

2.5 数值模拟过程

2.5.1 初始地应力平衡

Abaqus提供了两种地应力平衡方法，一种是通过软件Load模块用Predefined Field命令实现；另一种是通过软件中编辑关键字中的功能编辑代码添加，即将土层的初始应力值输入到input文件中来实现地应力的平衡。

2.5.2 初始孔隙比的设定

初始应力状态随着土层深度的变化而变化，其初始孔隙比也随之发生变化。这可通过Abaqus软件的用户子程序来实现初始孔隙比随土层深度的非线性变化。为此，结合初始等向固结曲线INCL的起点e1，找到当前状态在e—logp′空间的位置，确定初始孔隙比e0。这可在编辑关键字中输入“*initial conditions, type=ratio, user”，其中user是笔者编写的用于输入不同土层初始孔隙比的子程序。

2.5.3 计算参数确定及施工过程模拟

结合工程现场实际施工情况，塑料排水板采用C型板，其尺寸为120 mm×4 mm，渗透系数为4×10-4m/s，打设深度20 m，正方形布置，间距1.1 m。加固区土体采用修正剑桥模型进行模拟。该模型主要涉及3 个参数：κ，λ，M，其值可由等向压缩与膨胀实验确定(表1)。堆土采用线弹性模型模拟，其参数为：重度γ=15 kN/m3；膨胀角ψ=40°；泊松比ν=0.3；弹性模量E=20 MPa。

结合台州东部新区吹填土地基处理施工工况，道路区主干道的真空-堆载联合预压法处理数值模拟分析过程为：1) 地应力平衡；2) 砂垫层施工1 m，施工期10 d；3) 施加真空荷载至-85 kPa并恒载固结30 d；4) 堆填第一级宕渣1 m，施工期10 d；5) 恒载固结10 d；6) 堆填第二级宕渣1 m，施工期10 d；7) 恒载固结10 d；8) 堆填第三级宕渣1 m，施工期10 d；9)恒载固结90 d。

3 数值模拟结果与讨论

3.1 大、小变形下吹填土的沉降

地基土层的沉降值是判定加固区土体的固结情况、加固效果以及地基强度提高的重要指标。吹填土加固区地表中点处的沉降计算值与实测值随加载时间的变化曲线如图3所示。由图3可知：无论是采用大变形理论还是小变形理论计算所得土体地表沉降值与实测值变化趋势相同，都是随着加载时间的推移而逐渐增大，最后趋于稳定值。在施加真空预压荷载期间，分别采用大应变和小应变理论计算所得沉降值基本相同。随着地面堆土的逐步施加，采用小应变理论计算所得结果要大于大应变理论计算值且两者差异随着堆土高度的增加而逐渐变大，其中大应变理论所得结果与实测值更加接近。采用大变形理论计算所得结果要比采用小变形理论值要略大一些。采用大变形理论所得地表最大沉降为2.169 m，而小变形理论则为2.16 m，两者相差0.009 m。

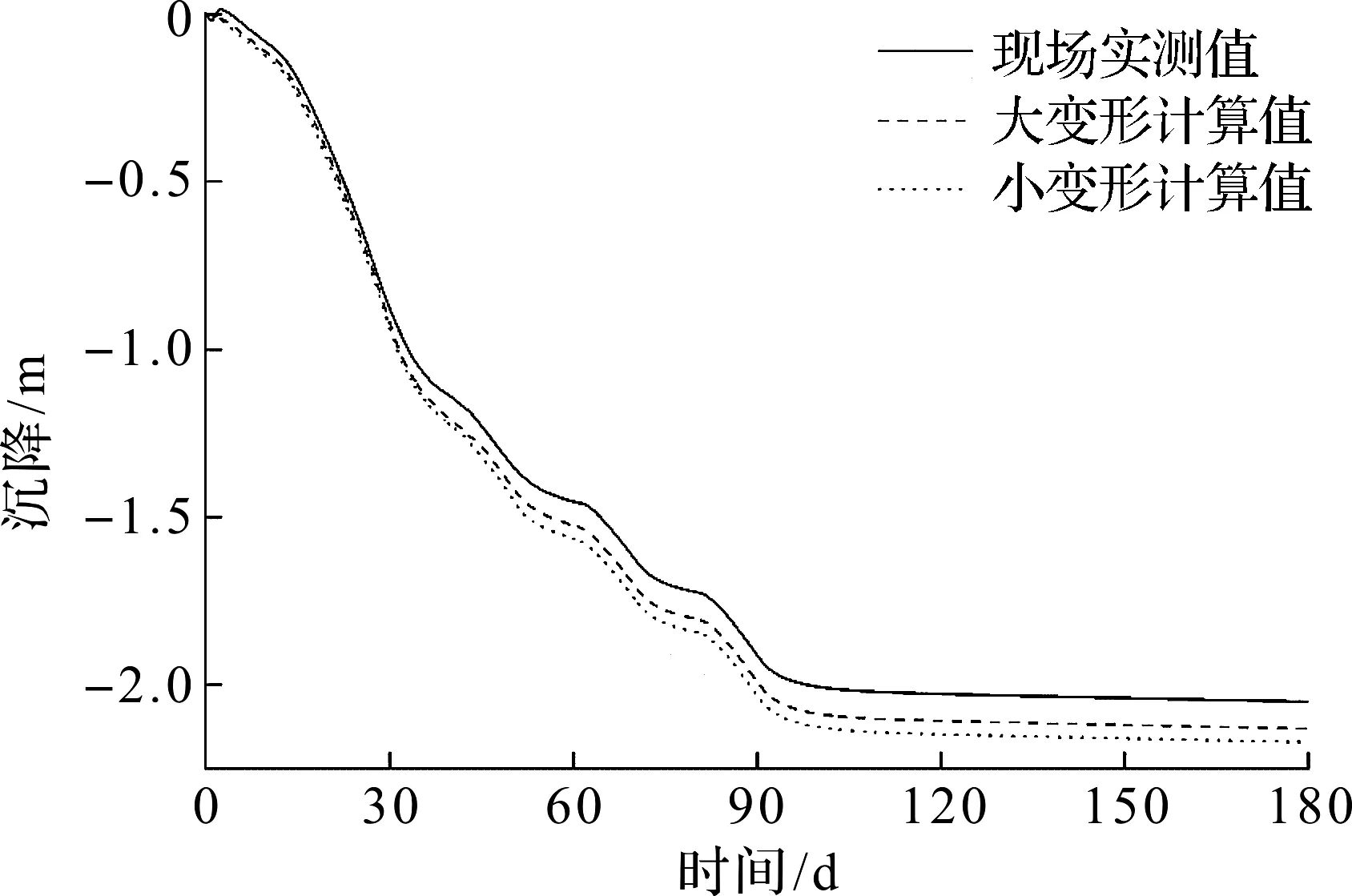
图3 加固区地表中点处沉降曲线

采用大变形理论和小变形理论计算所得加固区中心不同深度处的沉降变化情况如图4，5所示。由图4，5可知：采用大变形理论计算所得地基不同深度处的沉降值要略小于相应位置处的小变形理论沉降值，但两者差异不大，且随着深度的增加该差异值逐渐减小。

图4 大变形理论计算所得的分层沉降曲线

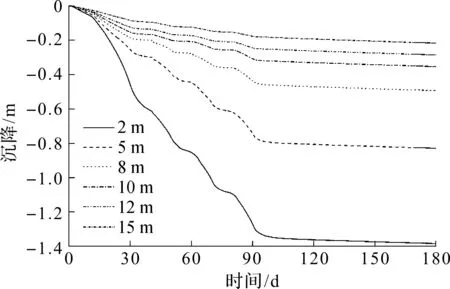
图5 小变形理论计算所得的分层沉降曲线

3.2 土体水平位移

在真空加载过程中，加固区土体会从影响区挤向加固区(其水平位移以负号表示)，而在堆载预压过程中则产生由加固区挤向影响区的趋势(其水平位移以正号表示)。离加固区边缘1.5 m处地表的水平位移变化情况如图6所示。由图6可知：随着砂垫层和堆载的施加，地表会产生向加固区外挤出的水平变形；随着真空荷载的施加则产生向加固区内的收缩变形，但由于堆载荷载小于真空荷载，地表土体仍有向加固区移动的趋势。采用大变形和小应变理论计算所得的变形值随加载时间的推移而逐渐产生差异，大变形理论计算所得水平位移更接近现场实测值，但两者的变化趋势和实测值一致。

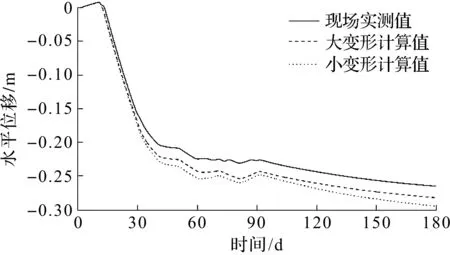
图6 离加固区边缘1.5 m处地表水平位移

采用大变形和小变形理论计算所得加固区边缘1.5 m处不同深度处的水平位移如图7，8所示。由图7，8可知：当加载时间小于40 d(即在地面堆载施加前)，同一深度处地基土体的水平位移达到最大，且为负值，表明真空预压会引起土体向加固区方向的水平位移(收缩变形)。但是，随着地面超载的施加和加载时间的推移，水平方向的收缩变形逐渐减小，这是由于地面堆土荷载会使地基土体产生向加固区外挤出的水平变形。由于真空荷载大于堆土荷载，此时地基土仍表现为产生挤向加固区的收缩变形，且该位移随着固结时间的增加而逐渐减小。当土层深度超过25 m后，该水平位移由负值变为正值，说明此时地基土体由加固区挤出，表现为侧向膨胀。采用大变形和小变形理论计算所得的水平位移曲线变化趋势一致，但数值略有差异。

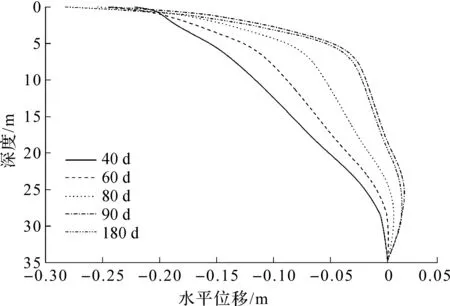
图7 大变形理论计算所得土体水平位移

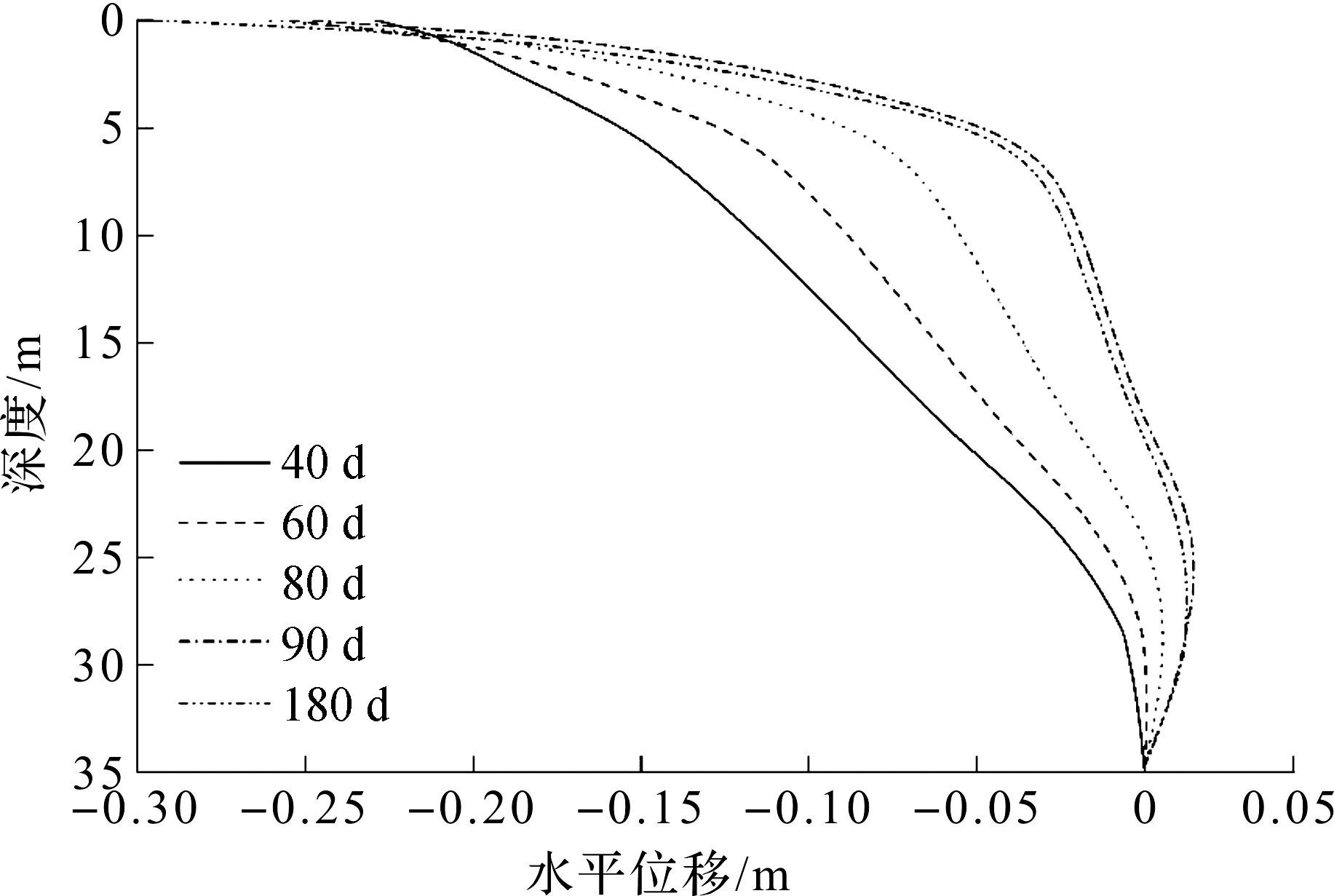
图8 小变形理论计算所得土体水平位移

3.3 超静孔隙水压力

考虑井阻效应后加固区中心处排水板不同深度以及距离排水板底1～2 m处的超静孔隙水压力随加载时间的变化曲线如图9所示。由图9可知：当t≤10 d(即施工砂垫层结束前)，任何深度处的超静孔隙水压力都为0，说明此时只存在静水压力。当t=10～30 d(开始施加真空预压)时，排水板深度范围内(0～20 m)各处的超静孔隙水压力因井阻效应降至不同值，然后保持稳定不变。地面堆载的施加对排水板深度范围内(0～20 m)的超静孔隙水压力的影响非常小。21～22 m处(即距离排水板底1～2 m处)的超静孔隙水压力在施加真空荷载后的的增加速度要比排水板内的要小，随后会因堆载的施加而产生波动现象，直到堆载结束后才慢慢下降至稳定状态。不考虑井阻效应的不同深度处超静孔隙水压力随加载时间的变化曲线如图10所示。由图10可知：发现排水板深度范围内(0～20 m)的曲线几乎一致，这是因为不考虑井阻效应后各深度的超静孔隙水压力均从0降到-85 kPa。21～22 m处的超孔隙水压力刚开始会增大，过了一段时间才会慢慢减小，这是由于在饱和土固结时出现了曼德尔效应。

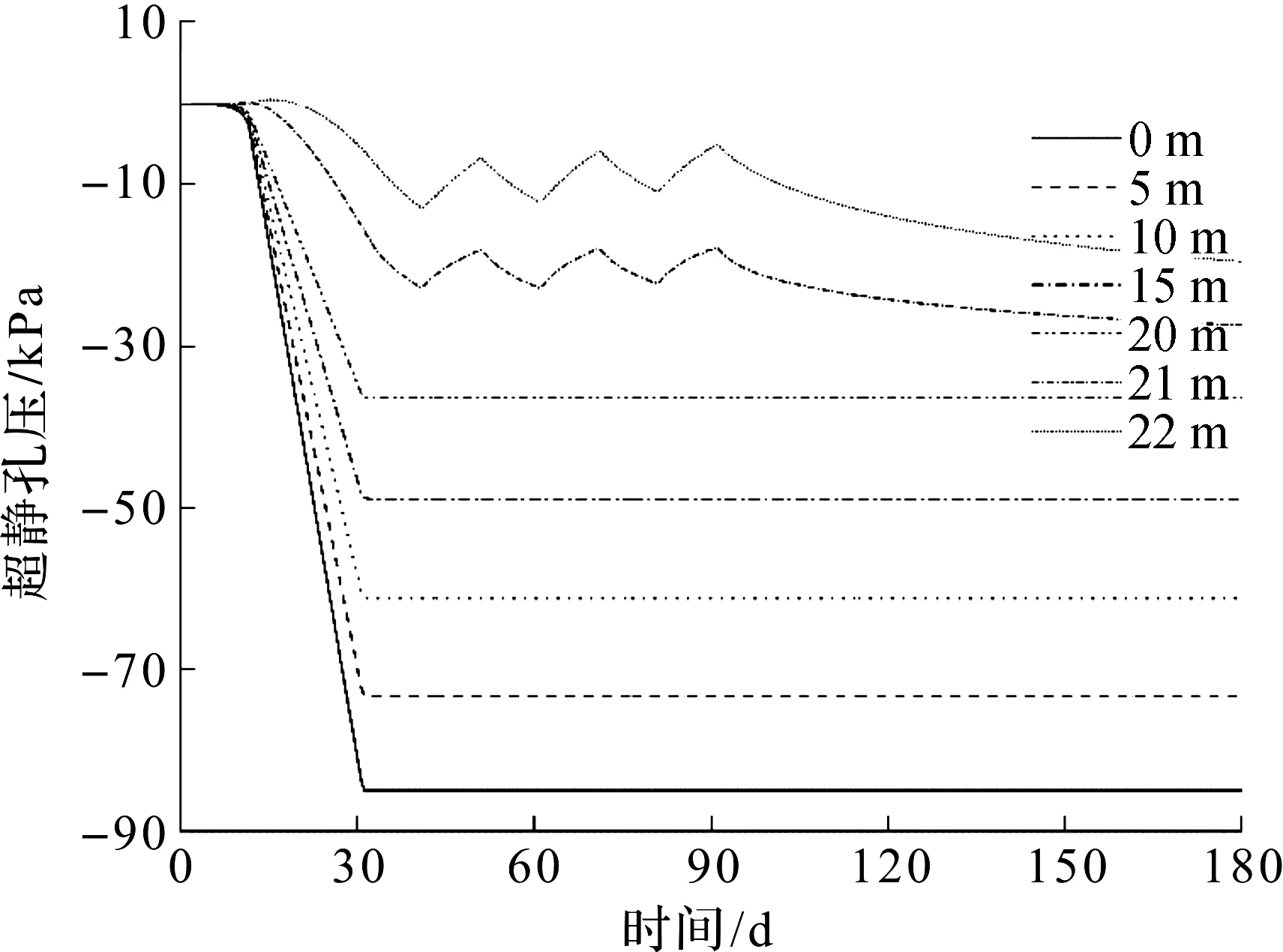
图9 考虑井阻效应的超静孔隙水压力随时间的变化

图10 未考虑井阻效应的超静孔隙水压随时间的变化

考虑与未考虑井阻效应的加固区中点下各深度处超静孔隙水压力随时间的变化情况如图11所示。由图11可知：除了地基表面以外，其余深度处考虑井阻效应的超静孔隙水压力均明显小于未考虑井阻效应的值。其中，图11(a)地基表面土体的超静孔隙水压力在受到真空荷载作用时不仅不会下降，反而会先上升，这同样反映出明显的曼德尔效应；图11(a，b)超静孔隙水压力的波动受地面堆载的影响较大，而图11(c)的影响则较小，在排水板范围内这种波动随着深度的增加而减小；对比图11(c，d)，在深度22 m处堆载引起的波动又变大了，这是因为深度22 m处在排水管深度范围以外，其真空度的传递远小于排水板深度范围内，故该处超静孔隙水压力的影响比20 m的要大。

图11 加固区中心不同深度处的超静孔隙水压力

4 结 论

采用数值模拟和现场实验的方法分析了真空-堆载联合预压加固吹填土地基的加固机理和沉降与超静孔隙水压力分布规律，分别采用大变形和小变形固结理论计算了土体的沉降、水平位移和超静孔隙水压力，并与实测结果进行对比分析。结果表明：采用大变形和小变形理论计算所得地基的沉降、水平位移以及超静孔隙水压力与实测数据吻合较好，且大变形理论计算值更接近实测结果，验证了将塑料排水板转换成砂墙进行计算是可行的；真空预压阶段的吹填土在加固区以内主要产生收缩变形而加固区以外则为剪切变形；真空-堆载联合预压阶段的加固区以外土体仍向加固区内部产生收缩变形，随着堆载的增加，加固区以外的土体会产生向上的隆起现象，井阻效应对加固区土体的超静孔隙水压力分布有较大影响；地面堆载的施加会使塑料排水板范围以外的土中超静孔隙水压力分布出现明显的曼德尔效应。