叶片数对泵作透平的外特性分析

杨加兵 童江波

（1.湖南工业大学 机械工程学院，株洲 412000；2.衢州学院，衢州 324000）

泵是可逆式旋转机械，泵反向用作透平称为泵作透平（Pump as Turbine，PAT）。泵作透平作为原动机，可以将流体的压力能转化为机械能，进一步产生电能。它可被用于城市智慧水网提取管道余压能为其余设备提供电力，还可以应用于海水淡化、石油化工以及小型水利发电等。PAT是减少能源浪费及开发新能源的重要举措，但目前对PAT的研究依然不够成熟。目前的研究主要集中在透平的选型、优化及流态稳定性，其中对透平叶片的研究是优化透平的重要措施及难点。

PAT最初由THOMA[1]等偶然发现。在透平中，流体通过冲击叶片使叶轮旋转，将流体介质的压力能转化为机械能，同时叶轮叶片与流体域工作介质相互作用，影响流体速度的改变和偏转[2]。YANG[3]使用CFX预测分析了PAT的性能，指出随着叶片数量的增加，透平效率提高，改善了内部非定常压力场。ADU[4]通过数值模拟得出，转速n=1 500 r·min-1时，4叶片PAT和6叶片PAT效率分别为57.8%和59.3%。PECZKIS[5]通过数值模拟和实验研究，对4叶片数和5叶片数的涡轮效率进行比较，结果显示4叶和5叶涡轮的效率分别为72%和84%，即5叶片数的涡轮可以更加高效地提取可再生能源。LI[6]研究了叶片数分别为22和32的径流式涡轮。研究得出，当叶片数为32时，涡轮流动状态平稳，不存在明显的流动分离和激波。

叶轮是影响透平能量转化的重要结构。本文对比研究了不同叶片数对泵和透平的性能，可以根据现有的流量信息选择现有合适的泵来用作透平使用，提高了压力能的回收。

1 计算模型

本文以M69-25离心泵为模型，图1为泵计算域模型，图2为透平计算域模型。透平的结构与泵的结构相同，只是工作时叶轮旋转方向与泵旋转方向相反，即进口为泵的出口，出口为泵的进口，流向相反。计算域由进口流域、蜗壳流域、尾水管流域以及叶轮流域组成。离心泵的主要结构参数为叶轮进口直径D1=62 mm、叶轮外径D2=160 mm、叶轮出口宽度b2=9.5 mm、蜗壳出口直径b3=50 mm。3种透平模型除叶片数外均相同，叶片数Z为5、7、9，如图3所示。

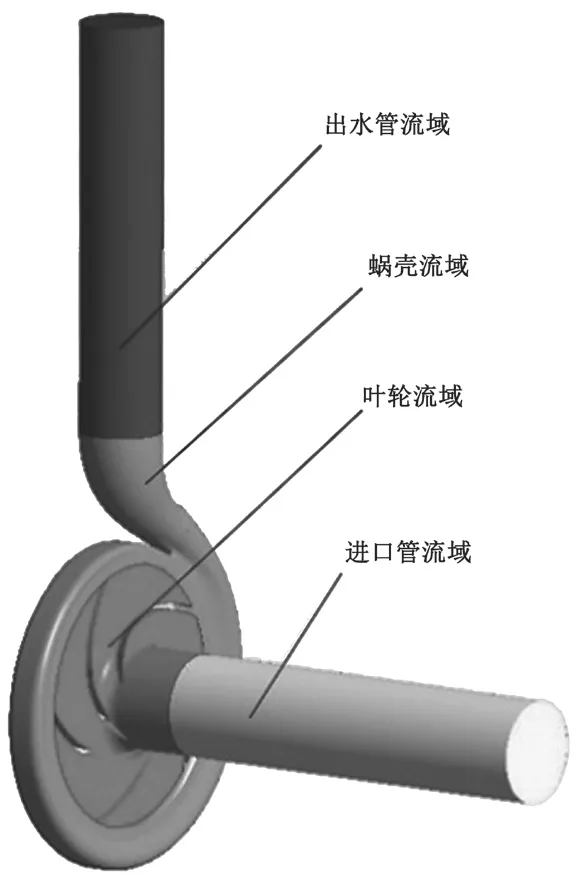
图1 泵模型计算域

图2 透平模型计算域

图3 不同叶片数的叶轮

2 数值模拟

计算流体动力学分析（Computational Fluid Dynamics，CFD）是通过计算机对流体现象进行数值计算，模拟流动现象。CFD的核心思想是通过数学方法使流场控制方程在一系列离散网格节点上求解数值解。本文采用的离散化方法为有限体积法，流体控制方程有连续性方程、动量方程和湍流方程。此外，计算时还需给定几何模型和边界条件。

2.1 网格无关性检测

有限体积法是将计算域离散成一系列网格。网格节点是网格体积的代称。网格数量和质量是影响模拟结果准确的两个主要因素。本文使用ICEM CFD划分网格，为保证数值模拟精确性，网格数量越多，数值模拟的结果越接近真实值。但是，较多网格数量要求较高的计算机性能，极大地增加了计算成本。为平衡数值模拟准确性和经济性，需对模型做网格无关性验证。通过增加模型网格进行数值模拟，当前后两次计算结果相差不大时，该网格数量可保证模拟准确性，此时看作数值模拟结果与网格数量无关。

结构性网格和非结构性网格对网格质量的影响不同。结构性网格质量高，需将模型拓扑成与模型相近的块，再将块细分成网格，应用于简单规则的模型，对复杂模型划分较难。非结构性网格可以离散复杂的模型，但需要较多的网格数量，对模型细节区域处理较好。

计算域由进口流域、叶轮流域、蜗壳流域和出口流域组成。模型进口流域和出口流域采用六面体结构性网格，叶轮和蜗壳流域采用非结构性网格。当泵扬程随网格数增加变化不大时，视为模拟与网格数量无关。模型的网格无关性验证，如图4所示。当网格数大于1 000 000后，泵的扬程基本趋于稳定，误差不超过1%。叶片数为5、7、9的模型，分别取1 537 753、1 437 639、1 407 864作为最终的计算网格数量。

图4 网格无关性

2.2 流体控制方程

2.2.1 连续方程

连续方程是流体的质量守恒定律的表达式，方程为：

式中：ρ是流体密度；t为时间；ui为坐标轴xi方向上的速度，i=1,2,3。

2.2.2 动量守恒方程

动量方程是描述流体系统力变化的方程，又称为N-S（Navier-Stokes）方程，表达式为：

式中，fi是坐标轴xi方向上的力，p是压力。

2.2.3 RNGk-ε模型

RNGk-ε能很好地模拟流体域中流体的流向。对强旋流和弯曲壁面的模拟较其他雷诺平均法二方程模拟结果更真实，表达式为：

式中：k为湍动能；μe为有效黏度系数；Pk为湍动能生成项；ε为耗散率，αk、αε、C1ε、C2ε为常数，且αk=αε=1.39，C1ε=1.42，C2ε=1.68。

2.3 边界条件设置

使用ANSYS CFX对泵和PAT性能进行数值模拟。叶轮流域为旋转域，其余部分为静止域。尾水管与叶轮、叶轮与蜗壳之间为动静交界面。泵转速n=2 900 r·min-1，透平转速n=-2 900 r·min-1，泵和透平边界条件使用流量入口和压力出口。流量取不同值，其他表面设置为壁面边界条件，壁面无滑移；湍流模型为RNGk-ε，进行定常计算，收敛精度为1×10-4。流体介质为25 ℃的水，密度为ρ=1 000 kg·m-3。

3 结果分析

数值模拟的结果，得到进口总压Pin和出口总压Pout。叶轮扭矩之和为M，得到透平在各个工况下的扬程Ht，计算公式为：

式中，g为重力加速度，n为转速。

得到叶片数Z为5、7、9的泵和PAT在不同流量下的扬程和效率，分别得到泵和透平流量-扬程和流量-效率曲线，如图5所示。

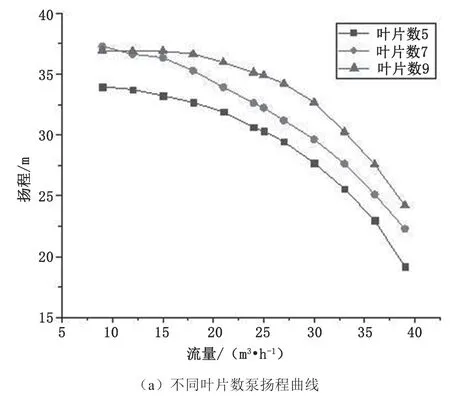
图5 不同叶片数外特性对比

图5（a）和图5（c）分别为泵的扬程曲线和效率曲线。可见，扬程随流量的增加不断下降，流量较小时泵扬程较大，此时能量转化效率较低。随流量增加，效率先增大后减小，达到一定流量时效率最大。泵在相同的流量下，叶片数为5、7、9的泵扬程依次增大，9叶片的泵效率大于5叶片和7叶片的效率。泵在流量Q=24 m3·h-1时，叶片数Z为5、7、9的泵效率分别为63.88%、63.91%、65.82%。可见，9叶片的泵效率比7叶片的泵效率提高2.9%，7叶片的泵效率比5叶片的泵效率提高0.03%。

图5（b）和图5（d）分别为透平的扬程曲线和效率曲线。随流量增大，PAT扬程不断增大；叶片数增加，扬程减小；在相同流量下，叶片数Z为5、7、9的透平扬程依次减小。随着流量的不断增大，透平效率先增大后逐渐趋于平稳。叶片数Z为5、7、9的PAT最佳效率点不同，最佳效率点对应的流量分别为39 m3·h-1、33 m3·h-1、36 m3·h-1，效率分别为77.44%、81.29%、84.17%。此外，增加透平叶片数可以有效提高透平效率。

透平扬程与泵扬程变化趋势相反，效率相差较大。不同叶片数的泵和PAT最佳效率点对应的流量不同，但增加叶片数，泵和PAT的效率都有增大。

4 结语

透平正常工作流量范围较泵的工作流量范围宽。大流量工况下，能量转化的效率对流量的波动不太敏感。流量在一定范围内波动时，依然能将大量压力能转化为PAT机械能。泵效率对流量变化敏感，工作范围窄，当泵的工作状态不在最佳工作点附近时，效率会迅速下降。叶片数是透平和PAT的重要能量转化部件，需根据正常工作条件选择合适叶片数的透平。叶片数增多，可以有效提高能量转化效率。此外，不同叶片数的泵和透平，最佳效率点不同，需根据来流流量选择合适叶片数的泵反转用作透平，以提高压力能的回收。