基于修正模型的电路板焊点疲劳寿命分析

曾芷筠,郭勤涛,潘 勇

(1.南京航空航天大学机电学院,江苏 南京 210016) (2.南京电子设备研究所,江苏 南京 210016)

电子设备通常是现代设备或系统的核心,在性能要求提高的同时,使用环境也变得更为严酷。在振动环境下,印制电路板(printed circuit board,PCB)光板和电子元器件之间将产生动态相对位移,在连接部位产生交变应力,导致焊点产生裂纹,加速失效[1]。有文献对电子设备的失效机理进行了分析[2],其中30%的故障是由于振动和冲击导致的,使得振动疲劳强度成为电子设备设计过程中保障可靠性的一项重要指标。

随机振动下零件的可靠性分析方法可分为时域法和频域法。Steinberg[3]通过分析功率谱密度函数,建立焊点位移与疲劳寿命的关系,提出了在振动环境下的失效物理模型。时域法的核心是基于循环计数法对危险位置的应力时间历程进行计数,计算量较大但较频域法更为准确。雨流计数法保留了应力幅值和平均值两个参量,能够真实地再现变幅循环载荷,是一种被广泛应用的寿命预测方法。Kim等[4]对塑料球栅阵列在恶劣随机振动和热载荷作用下的焊点可靠性进行了实验和数值分析。徐敏敏等[5]对机械结构危险点进行动态应力测试,运用雨流计数法对应力响应结果进行循环计数,预测疲劳寿命。钟嫄[6]开展随机振动封装结构损伤寿命评估研究,分别用雨流计数法、三带宽法和Dirlik 法对电路板危险位置进行应力幅值概率分布研究,并进行寿命评估。

由于焊点上的应力信号难以直接测得,因此用有限元仿真手段获取危险焊点位置的响应历程便显得很有必要。目前多数文献未对焊点位置的振动响应进行精确修正,将雨流计数法应用于电路板焊点有限元仿真的方法也还不够完善。本文应用基于灵敏度分析的模型修正方法对电路板相关参数进行校准,并通过随机振动试验验证了模型的精度。将试验中采集到的载荷谱用于瞬态响应分析,获得焊点的应力时域响应,并应用雨流计数法和Miner法则预计电路板的疲劳寿命。

1 附带器件电路板的动力学等效建模

1.1 附带器件电路板的模态试验

试验中将电路板用橡皮绳悬挂,边界条件视为理想自由状态,使用锤击法识别研究对象的模态参数,力锤作为激振设备对试件进行激励,且力传感器安装在锤头上,加速度传感器胶粘固定在PCB上,试验现场如图1所示。

图1 附带器件电路板的模态试验现场

1.2 电路板的建模及灵敏度修正

PCB光板尺寸为241 mm × 167 mm × 1.6 mm,主要材料为FR4环氧树脂,质量为126 g。根据PCB三维模型进行有限元建模,为保证仿真模型的计算精度,采用六面体单元进行网格划分,如图2所示。整体模型共有10 208个单元,PCB光板单元数量为4 787。初始材料参数见表1。

表1 有限元模型初始材料参数

图2 附带器件的PCB有限元模型

本文将PCB光板视作各向异性材料,Ex、Ey、Ez分别表示x、y、z向的弹性模量,μxy、μyz、μxz分别表示在xy、yz、xz平面内的泊松比,Gxy、Gyz、Gxz分别表示在xy、yz、xz平面内的剪切模量。查阅文献[7],设置PCB光板的初始材料参数,见表2。通过Speraman等级相关系数分析方法[8]筛选出重要的修正参数,可知电路板x向和y向弹性模量、xy平面剪切模量相关系数绝对值较大,因此将Ex、Ey、Gxy作为模型的待修正参数。附带器件的PCB光板的试验振型与仿真振型对比如图3所示。

表2 PCB光板的初始材料参数

图3 附带器件的PCB板前4阶试验、仿真模态对比

以模态试验的频率为目标,对仿真模型参数进行修正[9-10]。修正后的参数值为:Ex=20 043 MPa,Ey=22 284 MPa,Gxy=5 877 MPa。图4所示为迭代过程中各参数的收敛曲线,图5所示为模态频率值误差的收敛曲线。

模态修正结果见表3,可以看出,基于灵敏度的模型修正大幅度降低了模态频率值误差,使各阶模态频率值误差降到了1.1%以内。

表3 PCB光板修正前后仿真频率与试验频率对比

将电路板及连接的框架固定在激振器的激振杆上进行振动试验,应变片贴在电路板中心处焊点附近的位置用于测量应力。将振动试验得到的频率响应与仿真结果做对比,如图6所示。对修正前后的模型进行频响分析,发现修正后的模型极大地减小了频率误差,将误差从16%降低到6%。由于仿真和试验的频响基本相近,因此可以用此模型进行后续疲劳寿命分析。

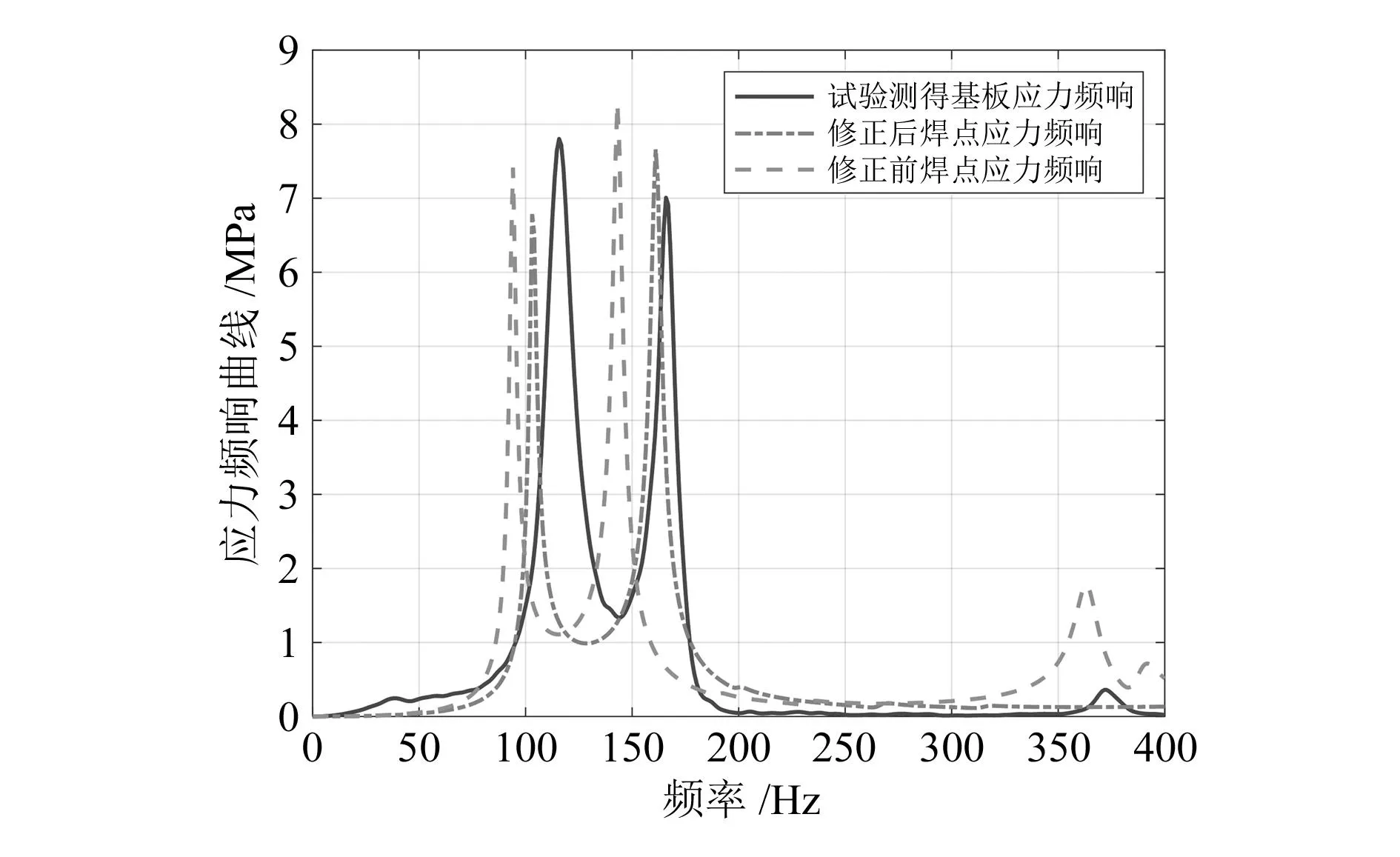
图6 随机振动试验和仿真频响对比

2 随机振动疲劳寿命预测

2.1 随机振动载荷谱的获取

对电子设备进行随机振动疲劳寿命分析,附带器件的电路板四条边和铝框之间通过螺栓连接。加速度传感器安装在电路板上,铝框架和激振杆之间安装力传感器用于采集激励信号,振动输入沿电路板的法线方向。采集的信号通过动态信号分析仪传输到计算机进行数据处理,现场图如图7所示。启动激振器,待运转稳定后采集180 s的信号数据,采样频率为1 024 Hz,激振信号带宽为5～400 Hz。

图7 激振器随机振动实验现场图

图8所示为采集到的激振力时域信号。将采集到的时域信号截取稳定状态下10 s的数据共10 240个点作为有限元模型的激励载荷,对修正后的仿真模型做频率响应分析。如图9所示,从元器件的6个焊点的同一位置各自选取一个单元输出应力响应,应力响应的频谱图如图10所示。可以看出6号焊点因为电路板的中心位置处的位移变化更大,焊点承受更大的交变应力。因此本文以6号焊点为危险位置点,对其进行疲劳寿命分析。

图8 随机振动实验激振力时域信号图

图9 焊点位置

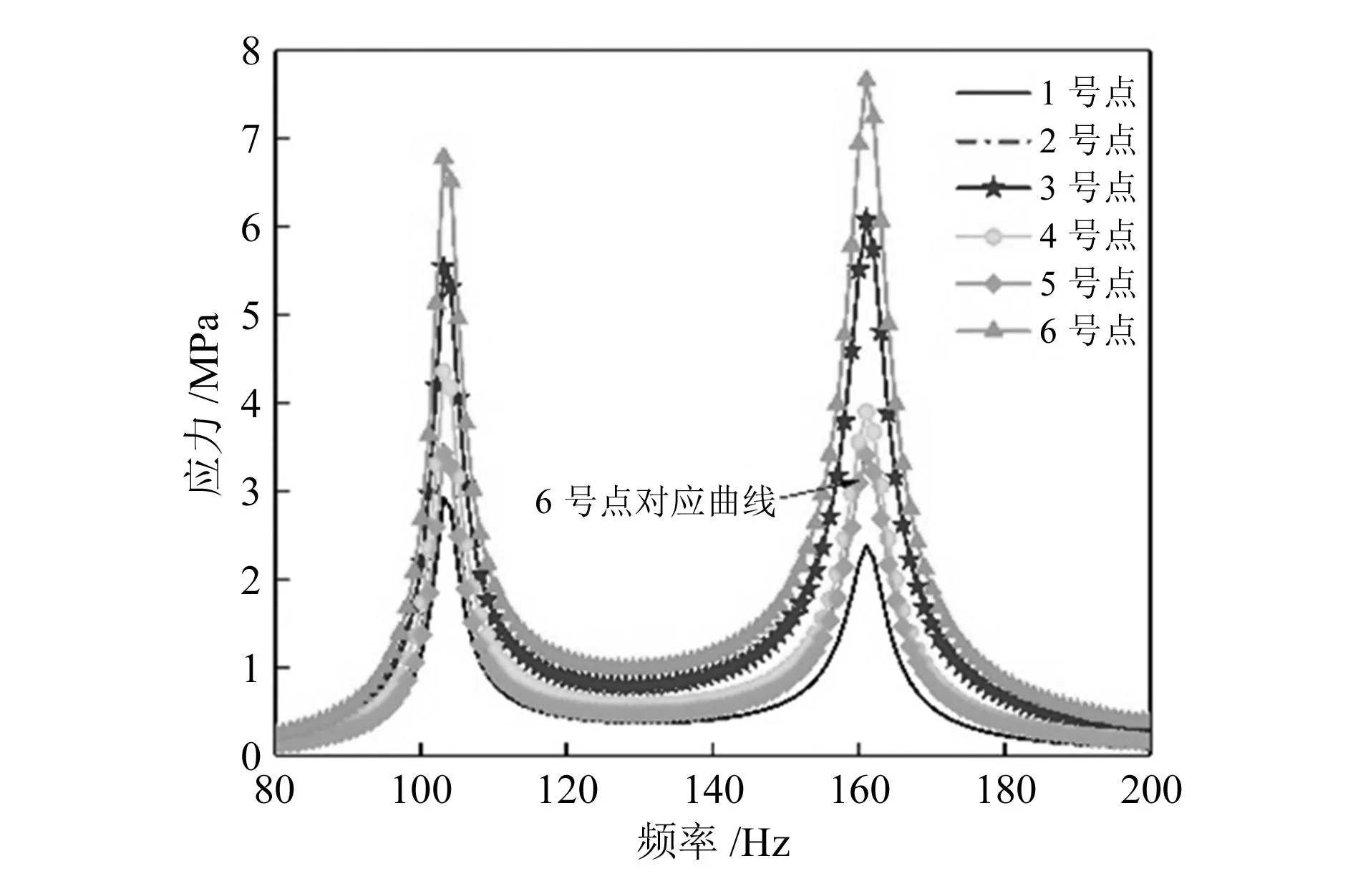
图10 各焊点的应力响应图

2.2 基于雨流计数法的疲劳寿命分析

雨流循环计数法[11]取垂直向下的坐标轴为时间轴,横坐标轴为载荷轴,模拟雨滴落到塔顶和从塔顶边缘落下的过程,记录应力循环的幅值和均值。

用2.1节实测出的10 s随机振动的应力谱,对电路板进行瞬态响应分析,图11为危险焊点10 s内的时域应力响应。

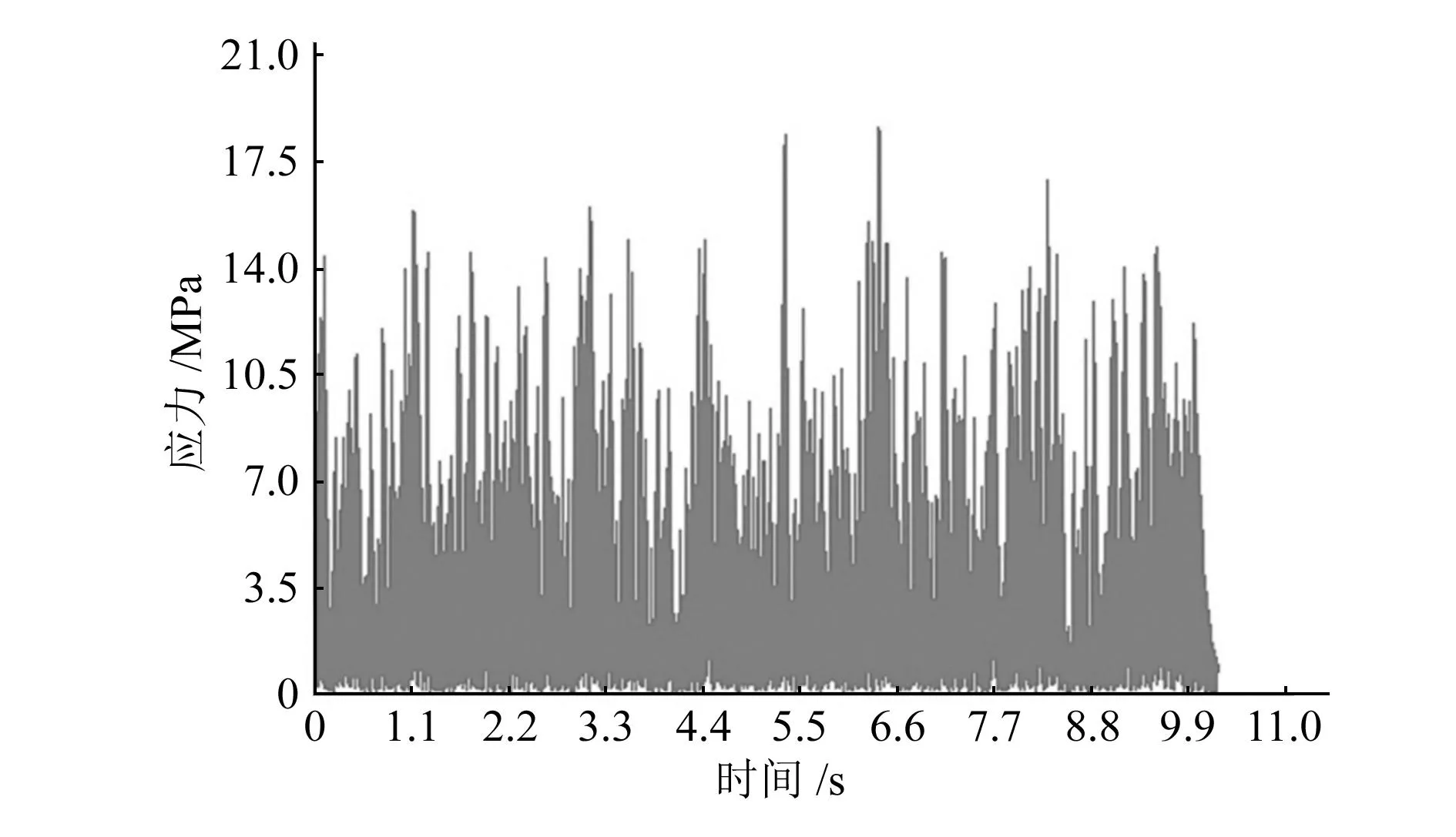
图11 PCB危险焊点的时域应力响应

对仿真得到的应力-时间历程进行雨流计数,记录每次循环的均值和幅值,图12为雨流计数法处理结果。将循环数据编成10阶二维应力谱。横坐标是从0.7 MPa到7.0 MPa共10个应力幅值,纵坐标是从0.36 MPa到6.89 MPa共10个应力均值。

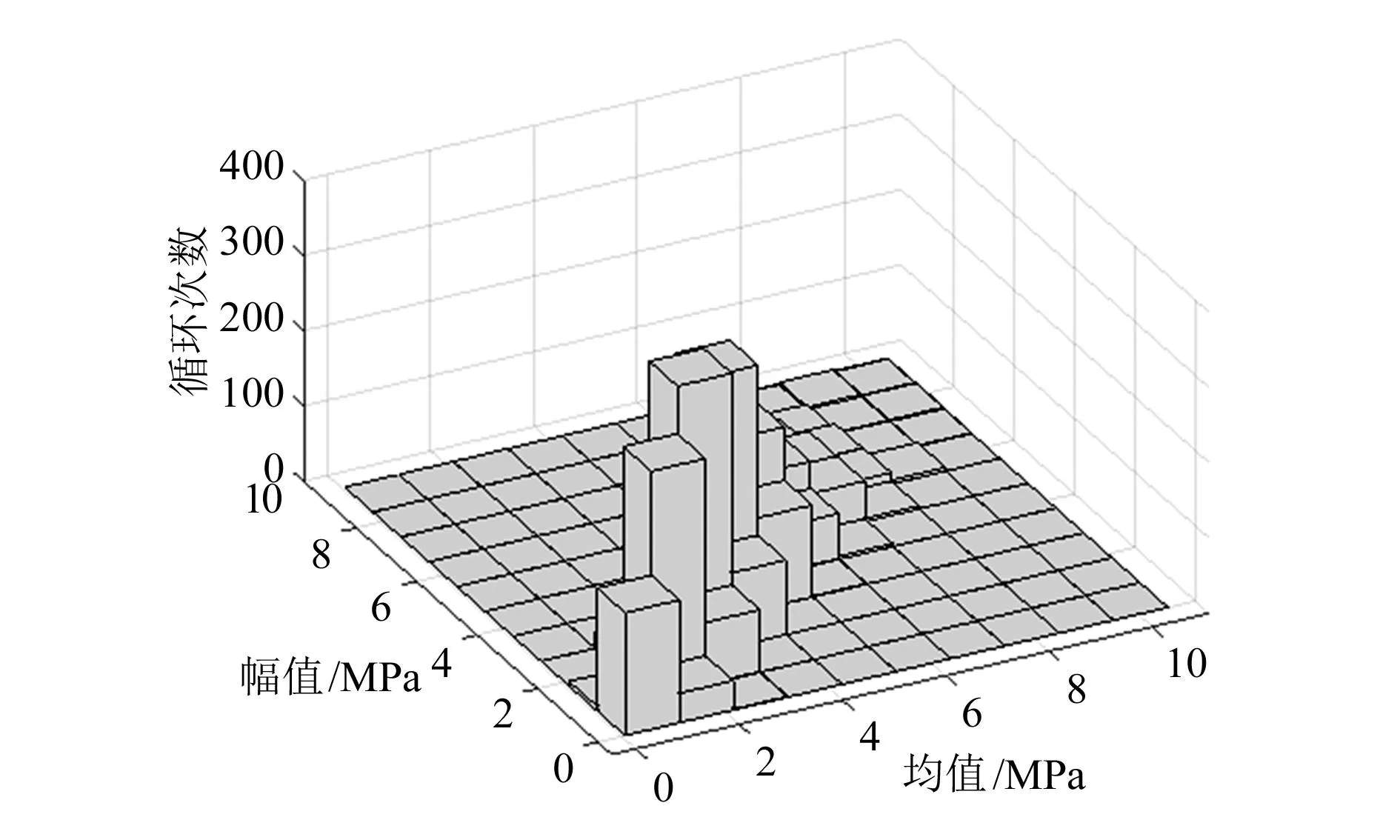
图12 雨流计数法处理结果

结构在非对称循环应力作用下,需要求得其等效应力。应用Goodman方程讨论在非对称循环变应力作用下的疲劳失效问题[12]。

(1)

式中:Sa为全循环应力幅值,Sm为全循环的平均应力,Se为全循环的等效应力幅值,Su为材料的抗拉强度。

由文献[13]得63Sn37Pb 焊料的抗拉强度为50.31 MPa,根据Goodman疲劳极限公式计算等效应力幅值。一般认为低于疲劳极限的应力对零件寿命的影响微乎其微,因此低于材料疲劳极限的数据忽略不计,于是得到的等效应力水平及其循环次数如图13所示。

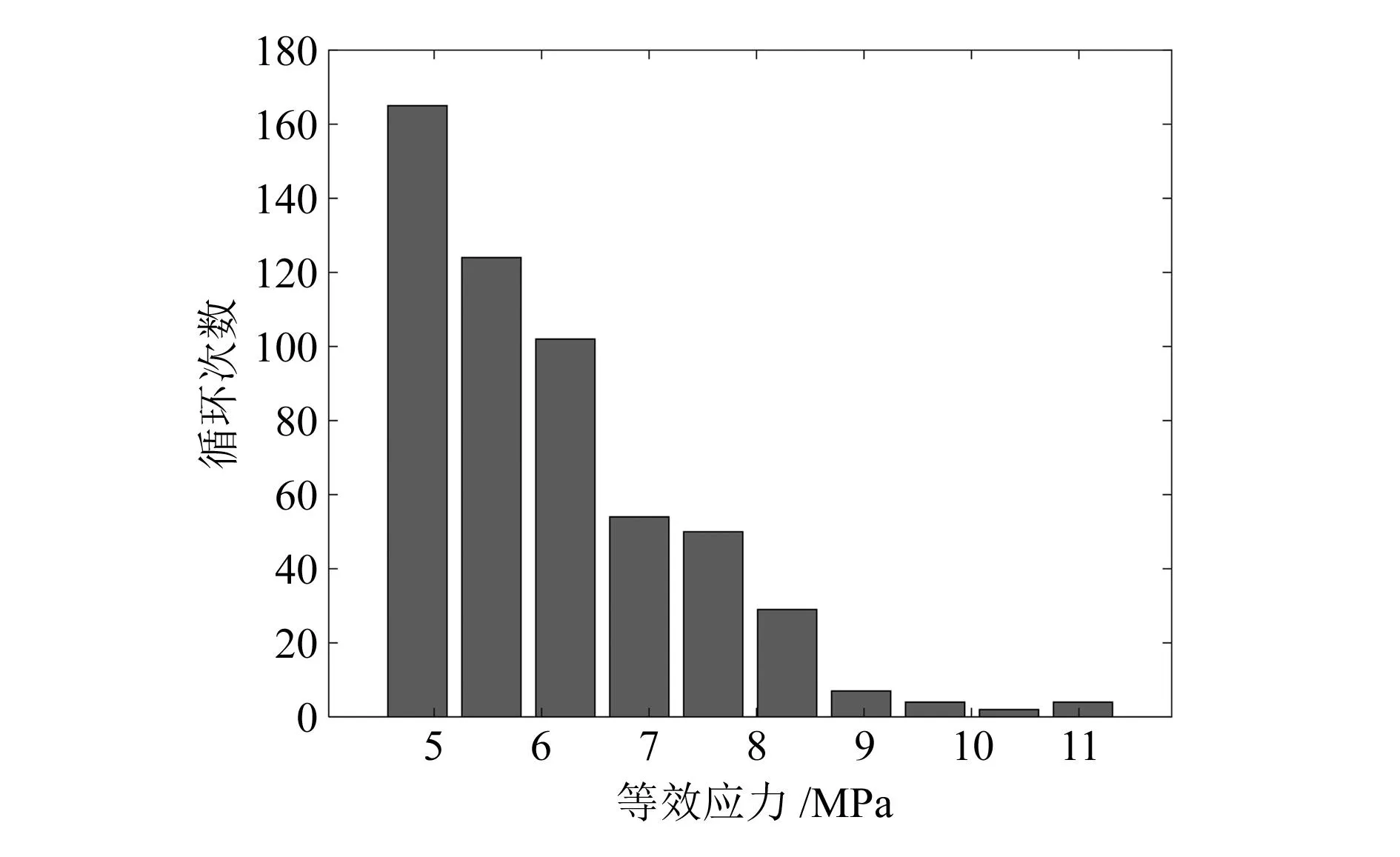
图13 等效应力水平及循环次数

Miner线性损伤模型准则认为,各个应力下的疲劳损伤各自独立,并且总损伤可以线性累加。零件在应力σ1水平下的循环次数为n1,N1是在该应力水平下材料破坏的总循环次数,在多个循环应力作用下,总的疲劳累积损伤可以表示为公式(2)。当疲劳累积损伤值D≥1时,则认为零件发生失效。

(2)

根据图14的63Sn37Pb 锡铅焊点的S-N曲线,得到材料在各个应力下疲劳故障前所需的循环数。根据Miner法则,利用式(2)计算出零件的累积损伤值:

图14 63Sn37Pb锡铅焊点S-N曲线

(3)

由前面分析得到的10 s内的应力响应造成的累积损伤值,可得出1 s内的累积损伤值D为2.349 8×10-5。根据得到的累值损伤值,可以求得危险焊点的预期寿命T如下:

(4)

对修正前的仿真模型进行疲劳寿命预估,修正前的模型累积损伤值为1.615×10-4,预期寿命为17.2 h,与修正后的模型相差了45%,修正后的累积损伤值更真实。

3 结束语

本文通过基于灵敏度分析的模型修正校准了有限元模型的各项参数和焊点的响应计算精度,并应用雨流计数法和Miner线性损伤累积法则,预计了焊点的寿命,对电路板的可靠性仿真分析具有一定的参考意义。但电子设备的失效机理是一个复杂的过程,本文仅针对振动失效展开研究,未考虑热应力、电应力的影响。后续可将热载荷分析加入仿真分析,模拟更真实的电路板工作环境。