时变计数法模型及其验证

范文亮，魏刚毅，李正良，2

(1.重庆大学 土木工程学院，重庆 400045；2.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045)

疲劳失效是航空工程、机械工程、船舶工程、交通运输工程和土木工程等诸多领域的普遍物理现象，由此造成的灾害性事故屡见不鲜。如飞机、核压力容器和桥梁等都存在严重的疲劳破坏风险[1]。众所周知，降低结构或构件疲劳失效危险的有效措施就是对其进行疲劳损伤分析，进而实现抗疲劳设计。

常规疲劳分析中，通常需要对所关注部位的应力时间历程进行统计，将此统计结果与疲劳累积损伤相结合即可获得结构或构件的损伤状态估计，由此可以进一步进行结构剩余寿命评估。其中，对应力时间历程进行统计进行统计的过程就称为计数，与之对应的方法即为计数法，是疲劳分析中非常关键的环节之一。

计数法种类繁多，主要包括水平跨越计数法(Level-Crossing Counting)、峰值计数法(Peak Counting)、单变程计数法(Simple-Range Counting)和雨流类计数方法(Rainflow Counting and Related Methods)等[2]。自1968年Matsuiski和Endo提出雨流计数法[3]以来，雨流类计数方法获得了广泛的关注，提出了三峰谷值法[4-6]和四峰谷值法[7-8]两大类方法，并在此基础上发展了很多改进措施[9-14]，目前已成为了应用最为广泛的计数法。仔细考察上述各类雨流计数法不难发现，尽管早期雨流计数法的各类缺陷逐渐被新近方法所改进，但是它们均存在一个共同的特点：欲获得某一时间历程的计数结果，必须从该历程的起始点开始运算。

随着可持续发展理念和精细化设计思路的重要性日益凸显，工程结构的全寿命周期设计近十年来引起了广泛的兴趣。显然，结构性能的时变变化规律和特性是全寿命周期设计的基础。对应于遭遇疲劳破坏风险的结构，结构的时变疲劳损伤分析就至关重要。换言之，需要了解结构疲劳损伤随着时间历程的变化。若采用传统的计数方法，任一时刻疲劳损伤的计算都需要从疲劳荷载刚作用于结构时开始计数，从而导致了很多不必要的重复运算，降低了计算效率。当需要由构件的疲劳损伤评估整体结构的疲劳损伤时，效率的下降就更为明显，对于复杂工程结构系统尤甚。

为了满足全寿命周期分析和设计的需要，借鉴动力分析中的增量方法思路，本文力图发展一种可以充分利用已有历程计数结果，再结合增量时程计数，从而实现任意时刻计数的时变计数法，并对其有效性和高效性进行验证。

1 时变计数法模型及实现

显而易见，对于一般的时间历程，若将其分为两段，且采用雨流计数法对整体和两分段分别计数，那么整体计数结果与两分段计数结果之和并不一定相等。以图1所示应力历程简单说明之。将该历程在图中虚线处分段，表1分别给出了图1(a)的计数结果和图1(b)中两段时程计数结果之和，两者存在显著差异。

表1 不分段与分段累加计数结果的比较

图1 历程不分段和分段两种情况

1.1 时变计数法模型

为解决上述问题，文中给出了时变计数法模型。详细过程如下：

(1) 可根据分析要求对时程进行分段。

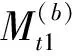
(4) 将第一段残波Rt1的后三个点接入第二分段ΔSt2的首部，形成新的第二分段ΔSt2’。若Rt1的点数不足三个，就Rt1将整体接入ΔSt2。

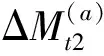
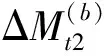
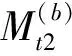
1.2 时变计数法的实现

根据时变计数法模型的阐述可以发现，除获得t1时刻的计数结果稍有差异外，其他时刻的计数结果的计算过程是完全相同的。因此，时变计数法的实现亦可分为两部分：首先是获得t1时刻的计数结果及其中间结果，然后逐步读入增量历程并采用建议方法获得其他时刻的计数结果。时变计数法的详细流程图见图2。

图2 时变计数法的实现流程图

2 时变计数法的计算性能分析

为了避免计算机运行状态和程序算法结构对各计数法运算效率的影响，文中将对时变计数法与Amzallag法所包含的各类操作数量进行简单的理论分析，并通过对比说明建议方法的高效性。

无论是建议的时变计数法和Amzallag法，计算过程均包含如下操作：数据检测和压缩、对给定时长的时程数据进行计数、残波复制和移位处理。假设上述各操作与对象的时间跨度呈正比，且单位时长的数据检测和压缩耗时为a，单位时长时程计数耗时为b，单位时长残波复制和移位耗时为c，且假设单位时长数据计数所剩残波的比例为d。

若存在一时长为[0,tn]的应力时程，需要获得在时刻t1，t2，…，tn的结构损伤。为此，必须先得到各时刻的计数结果。基于上述简单假设，考察分别采用时变计数法和Amzallag法所需的理论计算时间。

不难发现，采用Amzallag法对单位时长历程计数耗时为a+b+c+bd，于是所有n个时刻计数结果的耗时为(t1+t2+…+tn)×(a+b+c+bd)。

若采用时变计数法，则获得t1时刻的计数结果需耗时t1×(a+b+c+bd)；获得ti时刻的计数结果需耗时为(ti-ti-1)×(a+b)+Ai(a+b)+dAi(a+b+c)，其中Ai=di-1t2+di-2(t3-t2) +…+d(ti-ti-1)，总耗时即为各时刻耗时之和。

为便于比较，不妨再假设各时刻均匀分布，且间隔时长为τ，那么采用Amzallag法所需总耗时为n(n+1)τ/2×[a+(1+d)×b+c]；而采用时变计数法所需耗时为 [nτ+(1+d)A0]×(a+b)+(dA0+τ)c+dτb，其中A0=(n-1)dτ/(1-d)+[(1-dn-1)(1-2d)dτ]/(1-d)2。通常，d远小于1，随着n的增大，dn-1逐渐趋近于0，于是A0≈(n-1)dτ/(1-d)+(1-2d)dτ/(1-d)2。显然，Amzallag法的总耗时随n呈非线性增长，而建议方法耗时基本与n呈正比，且d越小，比例系数越小。因此，随着n的增大时变计数法的高效性逐渐显著。以n=100，d=0.5为例，Amzallag法的总耗时为5 050τ(a+1.5b+c)，时变计数法的总耗时为137.125τa+137.625τb+13.375τc，不足前者的1/37。若n=10 000，d=0.5，则建议方法耗时不足Amzallag法的1/3 600，高效性较n=100情形更为明显。

3 时变计数法模型的算法验证

文中针对两类简单算例，将建议方法与常用的雨流类计数法展开了详细的对比分析，以验证时变计数法的准确性。此处，常用雨流类方法选取两种，分别为Bannantine等提出的三峰谷值法(简称为Bannantine法)与Amzallag法。

3.1 随机应力时程

为简便，文中构造了一类虚拟的随机应力历程，其构造过程如下：首先生成m个服从N(0,1)分布的随机数据点，并将其视为有序数列，然后将该数列中的各元素依次交替乘以“-1”和“1”得到新的有序数列，最后以该有序数列为纵坐标(即应力值)、以从0开始的等间隔时刻为横坐标得到随机应力历程。

对于构造的变幅应力历程，可将其分为n段，由时变计数法给出n个时刻对应的计数结果，同时亦可由Bannantine法和Amzallag法给出最终时刻的计数结果。仅从验证时变计数法准确性的角度出发，只需给出最终时刻的计数结果并将其与常用计数法比较即可。

为了验证建议方法的普适性，文中生成了3条随机应力时程。采用上述各计数法对此3条历程进行计数的结果分别示于图3～图5。图中，x轴为滞回环的幅值，y轴为其均值，z轴为各幅值-均值对出现的次数，下同。

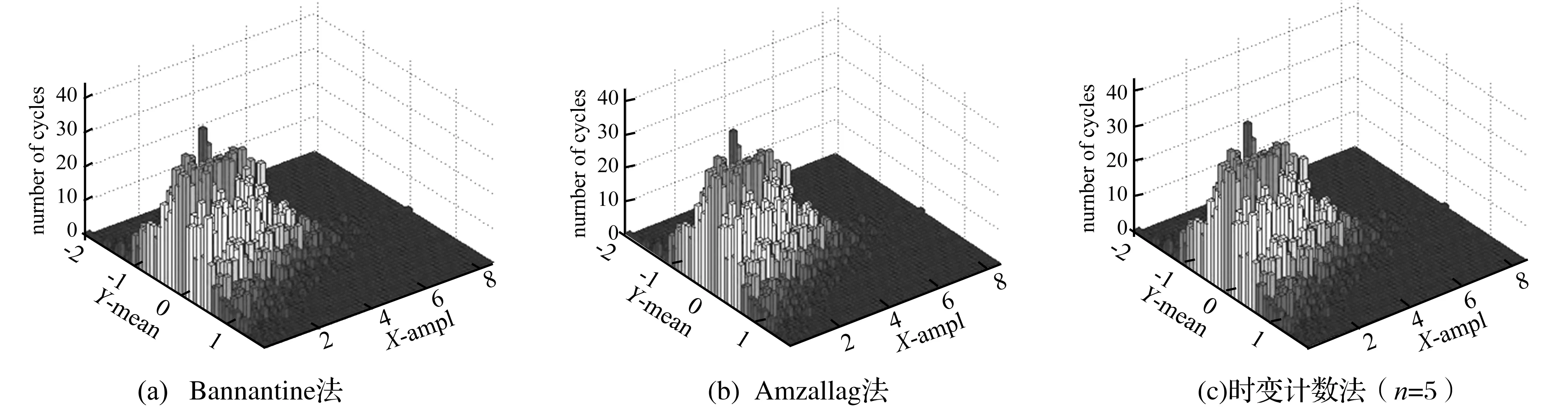
图3 随机应力时程1的计数结果(m=25 000)

图4 随机应力时程2的计数结果(m=50 000)

图5 随机应力时程3的计数结果(m=75 000)

不难发现，对于任意构造的3个随机应力时程，时变计数法的结果均与常用雨流类计数法的结果吻合，有效地验证了建议模型的准确性和合理性。此外，由上述3个算例亦可发现Bannantine法和Amzallag法的计数结果也是一致的，进一步验证了三峰谷值法与四峰谷值法的等效性，与McInnes等[15]的理论分析结果相互佐证。

值得指出的是，尽管各方法得到的幅值-均值对循环的出现频次完全相同，但各方法获得的幅值-均值对序列的次序不同。

3.2 一般应力时程

为了验证建议方法对更一般时间历程的适用性，文中截取了某输电塔关键构件在风致振动下的应力时程为计数对象。该时程共包含3 004个峰谷点，时间间隔0.25 s，总时长为751 s。采用时变计数法时，将其分为3段，即1～1 000、1 001～2 000和2 001～3 004这三段。由于Bannantine法和Amzallag法的等效性，此处仅给出Amzallag法和建议方法得到的最终计算结果，如图6所示。经比较，建议方法的准确性得到了进一步验证。

图6 输电塔应力时程的最终计数结果

图7 输电塔应力时程的时变计数结果

此外，在采用时变计数法获得最终计数结果的过程中可以很方便地给出前两段增量历程终点时刻的计数结果，如图7所示。

4 结 论

为了提高时变疲劳损伤分析的效率，文中借鉴动力分析中增量法的思路，提出了一种可以逐步读入增量时程进行计数的时变计数法。与传统计数法相比，该方法不仅可以获得最终时刻的计数结果，而且可以给出各增量时程终点时刻的计算效果。由于不必每次均从零时刻开始计算，时变计数法显著地改善了传统计数法在时变分析中的效率，且所关注的时点越多，效率提高就越为明显。最终，文中通过一个虚拟算例和一个实际工程算例验证了建议计数法的准确性。

此外，文中通过算例的形式验证了三峰谷值法与四峰谷值法的等效性，与McInnes等的理论分析结果是相吻合的。

[1] 张行，赵军.金属构件应用疲劳损伤力学[M].北京: 国防工业出版社，1998，1-2.

[2] ASTM E1049-85.Standard practices for cycle counting in fatigue analysis [S].West Conshohocken，Pennsylvania: ASTM International，2005.

[3] Matsuishi M，Endo T.Fatigue of metals subjected to varying stress [C].In Proceeding of the Kyushu Branch of Japan Society of Mechanics Engineering，Fukuoka，Japan (in Japanese)，1968，37-40.

[4] Downing S，Socie D F.Simple rainflow counting algorithms [J].International Journal of Fatigue，1982，4(1):31-40.

[5] Glinka G，Kam J C P.Rainflow counting algorithm for very long stress histories [J].International Journal of Fatigue，1987，9(3):223-228.

[6] Bannantine J A，et al.Fundamentals of metal fatigue analysis [M].New Jersey: Prentice-Hall，1990，193-196.

[7] Amzallag C，et al.Standardization of the rainflow counting method for fatigue analysis [J].International Journal of Fatigue，1994，16:287-293.

[8] 蒋荟.实时雨流计数法的“三变程”计数原则[J].航空计算技术，2008,38 (5):5-7.

JJIANG Hui.Three-range rule of real-time rain-flow counting method [J].Aeronautical Computing Technique，2008，38(5):5-7.

[9] Rychlik I.A new definition of the rainflow cycle counting method [J].International Journal of Fatigue，1987，9(2):119-121.

[10] Hong N.A modified rainflow counting method [J].International Journal of Fatigue，1991，13(6):465-469.

[11] Anthes R J.Modified rainflow counting keeping the load sequence [J].International Journal of Fatigue，1997,19(7):529-537.

[12] 朱亦钢.一种随机变化载荷的疲劳损伤累计方法[J].机械强度，2004，26(S):32-35.

ZHU Yi-gang.Damage counting algorithm for random load fatigue analysis [J].Journal of Mechanical Strength，2004，26(S):32-35.

[13] 田军，李强.改进的雨流法实时计数模型[J].北京交通大学学报，2009,33(1):28-31.

TIAN Jun，LI Qiang.Improved model of rain-flow real-time counting method [J].Journal of Beijing Jiao Tong University，2009，33(1):28-31.

[14] 蒋东方.雨流计数的递归算法[J].航空学报，2009，30(1):99-103.

JIANG Dong-fang.Recursive algorithm for rain-flow counting [J].Acta Aeronautica et Astronautica Sinica，2009，30(1):99-103.

[15] McInnes C H，et al，Equivalence of four-point and three-point rainflow cycle counting algorithms [J].International Journal of Fatigue，2008，30:547-559.