叶栅式反推力装置辅助导轨疲劳寿命预测
黄 婧,刘洪波,王谦舜
(中国航发沈阳发动机研究所,沈阳 110015)
反推力装置作为大型军、民用飞机上重要部件之一,可以显著缩短大型飞机的滑跑制动距离,提高机场的使用效率和飞机着陆安全性[1]。而辅助导轨是反推力装置上重要的运动部件,其性能好坏直接影响到整个反推力装置的安全性、可靠性和使用寿命。因此,在承受周期性载荷作用下合理地预测零部件的疲劳寿命十分必要,而在此过程中,必须对载荷时间历程进行统计处理。目前,常用的计数方法有单参数计数法、范围对法、称对法、雨流计数法等[2]。由于雨流计数法与现代计算机技术融合性能好、计算准确快速的特点,本文采用雨流计数法对薄弱部位的应力-时间历程进行统计处理,结合Miner法则和材料的S-N曲线,对某叶栅式反推力装置的辅助导轨疲劳寿命进行估算。
1 获取薄弱部位的动态载荷谱

图1 辅助导轨-导轨槽移动副有限元模型
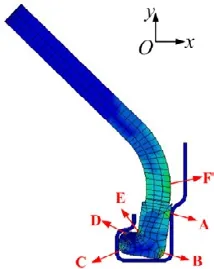
图2 辅助导轨薄弱部位示意图
本文针对某叶栅式反推力装置的辅助导轨-导轨槽,在ANSYS中建立其有限元模型(图1所示),通过LS-DYNA求解器对其动力学特性进行求解。计算结果表明,辅助导轨上A、B、C、D、E、F六处过渡圆角根部为薄弱部位(图2所示),提取薄弱部位的应力-时间历程曲线即各薄弱部位的动态载荷谱如图3所示。
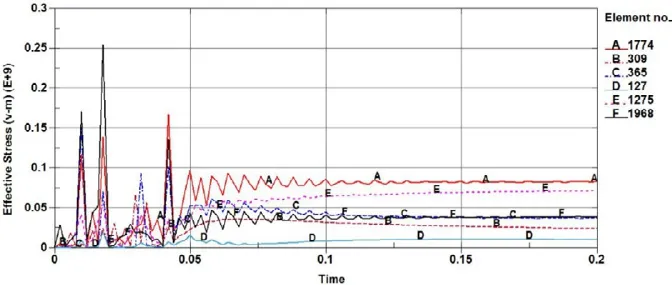
图3 辅助导轨薄弱部位应力-时间历程曲线
2 雨流计数法
雨流计数法是一种双参数计数法,可将实测载荷历程简化为若干个载荷循环,其计算规则为:
(1)找出应力-时间历程中的最高峰和最低谷,以绝对值大的点为起点;
(2)雨流依次从峰(谷)值的内侧向下流,直到更大的峰值(更低的谷值)停止流动;
(3)当雨流遇到上面流下的雨流时,则停止流动;
(4)根据上述规则,统计所有全循环或半循环,记录并计算各循环幅值和均值。雨流计数法示意图如图4所示。
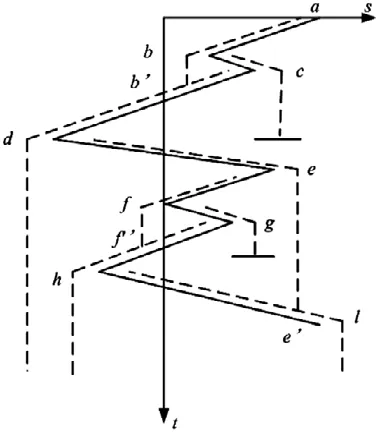
图4 雨流计数法示意图
将雨流计数法在计算机程序中具体实现过程如下[3]:
(1)数据压缩。首先,剔除相邻等值的数据点(如图5所示);其次,提取峰谷值组成新的数组,作为雨流计数法处理的数组(如图6所示)。
(2)循环数的提取。该阶段分为一次雨流计数、对接和二次雨流计数三个步骤:
a)一次雨流计数:在应力-时间历程中能提取循环的只有两种情况(如图7所示),其中a、b、c分别为其两端点值差的绝对值,若b≤a且b≤c,则提取一个循环图中三角形部分,并且剔除 E(i)和 E(i+1),保留 E(i-1)和 E(i+2),E(i-1)下标值不变,而E(i+2)的下标号从i+2开始整体提前2个变为E(i),即E(i)=E(i+1),否则保留E(i-1),并从下标开始进行下一组4个数据点的“四点法”的比较(如图8所示)。
b)对接:在一次雨流计数法提取循环数并记录之后,剩下的数据点构成的波形为发散-收敛型,此时按雨流计数法则无法再形成整循环,只能将其在绝对值最大点处截开再进行首尾对接。
c)二次雨流计数:将对接之后的波形,对其再次使用雨流计数法进行处理,再次提取循环数直到剩下最后3个数据点为止,最后3个数据点组成一个循环。至此,整个雨流计数法程序完成。
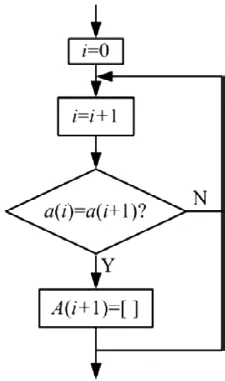
图5 雨流计数法等值压缩流程图
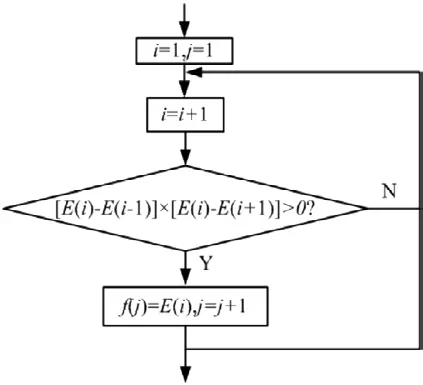
图6 雨流计数法峰值检测流程图
图9是以辅助导轨薄弱部位A为例,运用雨流计数法对其动态载荷谱进行统计的计算结果。(a)中第一幅为辅助导轨薄弱部位A处动态应力-时间历程,(a)中第二幅图为经一次雨流计数后未能形成全循环的点,(b)为最终雨流计数统计的计算结果,对于薄弱部位A经统计共得到35个全循环及其应力幅值和应力均值。
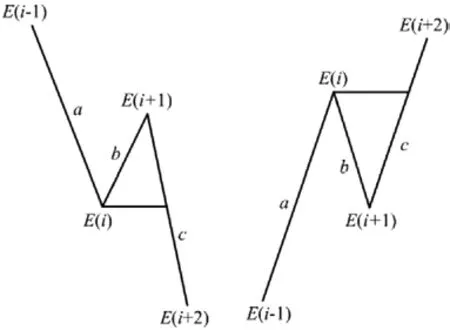
图7 循环数的提取
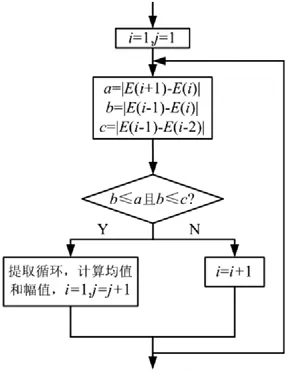
图8 雨流计数法提取循环的流程图
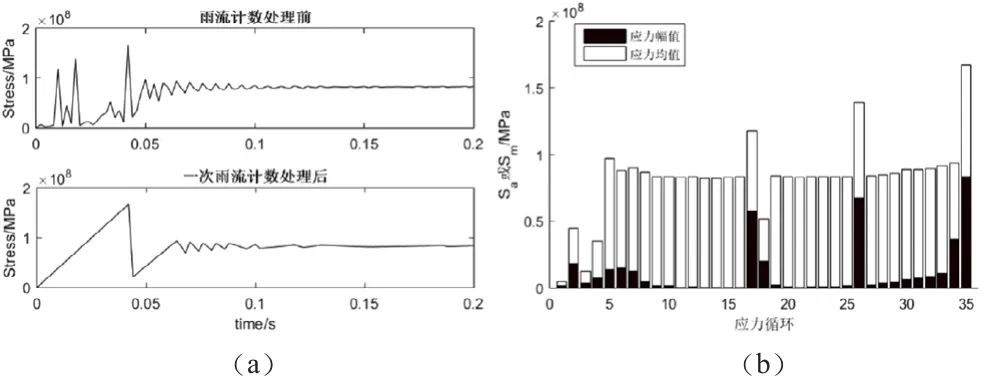
图9 薄弱部位A处动态应力雨流计数法统计结果
3 疲劳寿命预测
3.1 平均应力修正
通过雨流计数法统计后得到的载荷谱是基于非零平均应力的应力循环,计算疲劳寿命前应将其等效为零平均应力的应力循环,常用的等效转换有Gerber抛物线和修正的Goodman关系两种方式(如图10所示)[4]。
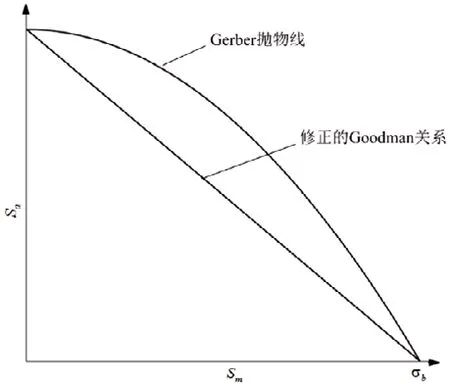
图10 考虑平均应力的修正曲线
Gerber抛物线满足以下公式:

式中,Sij为等效零均值应力;Sai为第i个应力幅值;Smj第j个应力均值;σb材料的强度极限,对于辅助导轨的铸铝材料σb=440MPa。
修正的Goodman关系疲劳经验公式为:

3.2 疲劳累积损伤量及其寿命估算
疲劳曲线在其有限寿命范围内的曲线方程为:

式中,C,m为材料常数,由疲劳实验确定。对于辅助导轨的铸铝材料,取C=6.647×1025,m=9.901[5]。
本文采用Miner准则[4]来计算辅助导轨的疲劳损伤量及寿命。根据Miner准则(又称线性累积损伤假设),施加应力幅值为Sa1的n1个载荷循环,就等效于消耗了疲劳抗力的n1/N1(N1是对应着应力幅值Sa1的疲劳寿命),同样的假设适用于后续任何载荷循环块,因此所有载荷循环的总损伤为:

当D=1时,认为结构发生疲劳破坏。疲劳寿命Nf=1/D。
由式(1-4)求得辅助导轨各薄弱部位的疲劳寿命如表1所示,其中当Nf>1×107时,可认为该处为无限寿命。计算结果表明,基于Goodman修正关系相比Gerber抛物线修正计算的寿命偏保守,而对于辅助导轨结构,A、C、F三处疲劳寿命小于1×107,其中A处疲劳寿命最小,为辅助导轨的疲劳寿命,即反推力装置展开6.9044×105次时,辅助导轨将发生疲劳破坏。

表1 薄弱部位疲劳寿命计算结果
4 结束语
本文以某叶栅式反推力装置辅助导轨为研究对象,在对其进行动力学特性分析获取薄弱部位动态载荷谱的基础上,采用雨流计数法对薄弱部位一个展开行程的应力-时间历程曲线进行处理,得到相应的应力循环幅值和均值,结合Miner法则和材料的S-N曲线,估算了辅助导轨各薄弱部位的疲劳寿命。计算结果表明,辅助导轨上薄弱部位A处的疲劳寿命最小,最易发生疲劳破坏,该接触部位是辅助导轨和导轨槽衬套结构设计和优化的重点。本文的研究成果对实际工作中有效预防和避免辅助导轨疲劳失效,避免事故发生具有重大意义。

