基于编制载荷谱的固体发动机药柱疲劳损伤分析

刘磊，李高春，刘著卿，李金飞

（1.海军航空大学，山东 烟台 264001；2.91458部队，海南 三亚 572000）

对于装载于海上作战平台的固体发动机而言，其先后要经历生产制造、无损检测、道路运输、洞库贮存、海上值班和发射等过程，其中，洞库贮存和海上值班经历的时间最长。海上值班时，部分大型固体发动机能够实现对温度和湿度较好的控制，但装载于平台的固体发动机时刻受到海洋波浪的作用，产生的低频振动是无法人为控制的。海洋波浪引起的振动是不具有明显规律的复杂随机载荷，难以通过数学公式对其进行表述，研究海洋值班条件下振动对固体发动机装药带来的影响往往需要较多的实测数据。由于舰艇上设备存储容量有限，进行长时间振动数据监测难度较大。

工程上常用载荷谱来进行结构的疲劳设计以及振动疲劳计算。编制固体发动机振动载荷谱主要通过对部分实测载荷数据进行数据处理和统计学分析，获得长周期内所承受载荷的幅值和频次信息[1]。自Ernst[2]提出标准程序载荷谱以来，程序疲劳试验法在工程中得到了广泛应用。随着液压伺服控制精度的提高，利用随机疲劳载荷谱对不规则载荷进行模拟的技术得到重视[3]。Johannesson[4]在2001年提出了基于雨流计数的非参数密度估计方法，并通过汽车测量信号进行了验证。高天宇等[5]应用非参数雨流外推方法编制了某型装载机液压缸的载荷谱，进而设计了全作业段程序加载谱。李妍[6]使用改进的非参数雨流外推方法建立了轮式装载机的载荷谱，证明了全带宽非参数模型外推性能优于单带宽非参数模型。

本文利用某固体发动机实测振动载荷数据，通过非参数雨流外推方法获得了长周期条件下发动机循环载荷的幅值-频次信息，应用雨流重构法构建了固体发动机振动时的域载荷谱。

1 数据采集与预处理

1.1 数据采集

为获取某固体发动机值班时的环境数据，首先对发射贮运箱内的振动载荷进行实测，采用1C301型电容式三向加速度传感器采集振动数据。安装时，将传感器粘接于发射贮运箱内壁。考虑到长期监测的需求与存储容量的限制，对振动数据采用间断性采集，设置采样频率为400 Hz。振动传感器三个方向的坐标设定符合笛卡尔坐标系，x轴正向表示主航向，y轴正向表示水平面内主航向逆时针旋转 90°方向，z轴正向表示垂直向上方向。

通过前方数据传输，获得了某固体发动机在海上常规巡航时的6个采集样本，样本量见表1。

表1 监测数据Tab.1 Monitored data

1.2 数据预处理

1.2.1 消除趋势项

趋势项是指在长期环境温度等因素影响下造成的传感器监测数据偏离原始基线的现象，数据处理的第一步就是要消除长周期趋势项，使信号在零线附近变化。采用较为常用的多项式最小二乘法来消除趋势项，该方法通过解线性方程组来求出待定系数，具体算法见文献[7]。

1.2.2 数字滤波

研究表明，舰船在海浪、潮涌等载荷作用下的低频振动频率范围为0～5 Hz[8]。因此，使用带通滤波器提取监测样本在 0～5 Hz频率范围内的振动信息。以样本1的监测数据为例，图1给出了消除趋势项及数字滤波处理前后的数据结果。

分析图1可知，原始采集数据由于叠加了高频噪声信号而显得杂乱无序，同时在x轴、y轴采集信号中存在多处极端幅值点。经过消除趋势项和滤波处理后，x、y、z三轴振动数据呈现出较为明显的振荡波形，部分极端大幅值载荷也得到滤除。

从数据处理后的PSD曲线图可知，在样本1的采集时间段内，振动信号的主要频率集中在0～0.5 Hz之间。其中，x、y轴功率谱密度极大值对应的频率为0.2 Hz和0.4 Hz，z轴功率谱密度极大值对应的频率为0.3 Hz。

1.2.3 消除奇异点

处理信号时出现幅值远远偏离左右两点的数据点称为奇异点，奇异点的存在会使振动曲线产生尖锐毛刺。Ncode软件中的奇异值探测模块提供了对奇异点的探测和消除功能（如图2所示），探测到的奇异点可以直接删除或者用周期信号代替[9]。载荷数据中奇异点的探测方法主要有梯度门限法、幅值门限法和标准方差检验法，分别对应软件模块中的Differential、Amplitude、CrestFactor三种算法。通常需要使用两种及以上的方法来清除毛刺，对采集的样本数据使用多种算法进行处理，共消除奇异点71个。

图1 原始信号与数据处理后的信号Fig.1 Raw signal and signal with processed data: a) raw data; b) x axial data after processing;b) y axial data after processing; c) z axial data after processing

图2 软件滤除奇异点操作过程Fig.2 Filter-out of singular points with software

1.2.4 数据拼接

将经过完全数据处理的 6个样本的振动数据进行拼接，组成非参数雨流外推的输入载荷。拼接时，为避免每段载荷连接处出现奇异点，对拼接数据段需要再一次做剔除奇异点处理。剔除奇异点后的拼接载荷段如图3所示。

图3 振动加速度载荷Fig.3 Vibration acceleration load

2 载荷谱编制

以拼接载荷数据为基础，进行振动载荷谱的编制。载荷谱的编制主要包含三个内容：载荷频次统计、载荷外推和载荷重构。载荷外推是载荷谱编制流程中的重要一环，是指运用数理统计的方法，将测得的短时载荷扩展至全寿命周期载荷。雨流矩阵外推法能够实现频次和载荷的双向外推，其中，雨流矩阵非参数外推法可以避免参数法难以用已知分布拟合雨流矩阵的问题，对于随机载荷的外推效果更好。因此，采用雨流矩阵非参数外推法进行振动载荷的外推。

2.1 载荷频次统计

载荷频次统计一般采用的是循环计数法，该方法将复杂的时间-载荷历程进行简化，运用统计学方法，重点研究复杂波形中某些量值出现的频次。常见的幅值计数法有峰值计数法、雨流计数法、穿级计数法等。其中，雨流计数法能同时统计载荷的幅值和均值，且能较好地表现载荷变化对疲劳损伤的效应，因而得到了广泛应用。分别对x、y、z三轴“from-to”形式的雨流结果进行统计，得到的雨流直方图如图4所示。

图4 三轴雨流矩阵直方图Fig.4 Triaxial rainflow matrix histogram: a) x axix;b) y axis; c) z axis

2.2 载荷外推

非参数雨流外推的过程建立在核密度估计方法和蒙特卡洛法之上。核密度估计法本质上是以二维“from-to”形式雨流直方图上所有的实测数据点为核心、以带宽h为边界的概率密度估计算法[10]。非参数雨流外推算法的具体过程分为三步。

1）计算初始估计。

通过固定带宽的二维核估计方法获得所有数据点(x,y)处的初始概率f(x,y)。

式中：n为数据点个数；h为初始带宽，一般通过经验公式获得。

2）对雨流矩阵进行自适应核密度估计。

在非参数外推过程中，极端载荷附近的数据点比较稀疏，一般需要设置较大的带宽，小幅值区域的载荷密集，一般设置较小的带宽。依据以上思路，使用自适应核密度估计方法对样本数据的概率密度分布进行重新估计。

式中：λi为自适应带宽因子；h*为自适应带宽。

λi和h*是自适应核估计算式中最主要的两个参数。自适应带宽因子λi通过第一步中的初始核密度估计来计算，相应的计算公式如式(3)。

与初始估计带宽h不同，自适应带宽h*的确定需要以幅值-频次曲线中的载荷极值Rmax为限制条件，通过迭代运算求解得到。

3）运用蒙特卡洛法进行模拟，得到外推后的雨流直方图。

进行载荷外推时，需要选取一个合适核函数来进行概率密度估计。Ncode雨流子程序中内置了四种在水平面内投影的核函数：圆形核函数、基于均值的椭圆形核函数、基于幅值的椭圆形核函数及 Epanechenikov核函数，分别如图5所示。由于Epanechenikov核函数综合考虑了载荷分布中均值和幅值对外推结果的影响因素，且其概率分布模型与雨流矩阵具有良好的适应性[11]，因此采用Epanechenikov核函数对雨流矩阵进行概率密度分布估计。

经验理论认为，经历106次循环载荷，对包括极少发生的高幅值载荷之内的全部载荷具有足够代表性[12]。将载荷累计频次外推至106次，外推因子k为：

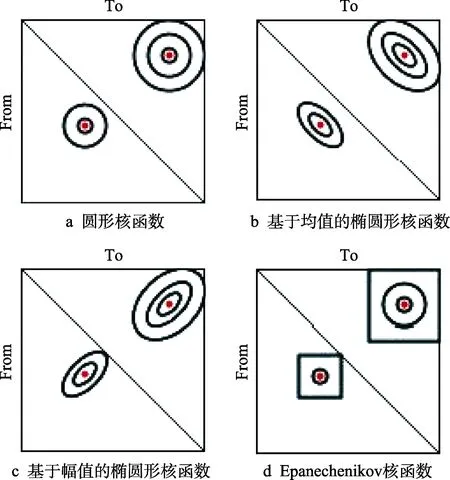
图5 四种形式的核函数Fig.5 Four forms of kernel functions: a) circular kernel function; b) elliptic kernel function based on mean value;c) elliptic kernel function based on amplitude;d) epanechenikov kernel function

式中：Ni为某工况原始累积频次，为某工况外推后的累积频次。

得到外推因子k后，运行雨流外推子程序，得到x、y、z三轴外推频次曲线和外推后的雨流直方图，分别如6和图7所示。由图6可知，非参数雨流外推实现了载荷频次与幅值的双重外推，外推后的x、y、z三轴的极值载荷分别提高了51%、83%、115%，实现了分段监测数据中未涵盖的更加严酷的振动载荷的量化表示。

由图7可知，外推前后“from-to”雨流分布图载荷数据点均主要分布在小幅值的中心区域；外推前较大的载荷幅值主要呈沿幅值和均值的交叉十字分布，外推后十字形分布得到平滑，呈现类似矩形的区域分布，且中心区域的小幅值载荷更加集中。

2.3 载荷重构

对雨流外推后的载荷进行时域外推的方法称为雨流矩阵模拟法。该方法基于以下基本原则：新序列必须呈现与先前序列相同的雨流计数结果，载荷重构过程相当于载荷循环提取的逆过程，将提取的载荷循环插入到时间序列中。如图8所示，将幅值划分为等间隔的几行，从下到上行数依次递增，载荷起始点所在位置称为行数（row），载荷转折点所在位置称为列数（col.）。一般称插入到时间序列的载荷循环为插入循环，ri、ci分别是循环载荷的行数与列数；接收插入循环的时间序列为接收循环，rr、cr分别是其行数与列数。雨流重构主要有如下4种规则[13]。

图6 外推频次曲线Fig.6 Extrapolation frequency curve: a) x axis; b) y axis; c) z axis

图7 外推前后的雨流直方图对比Fig.7 Comparison of rainflow histogram before and after extrapolation: a) before extraplolation of x axis; b) before extraplolation of y axis; c) before extraplolation of z axis; d) after extraplolation of x axis; e) after extraplolation of y axis; f) after extraplolation of z axis

1）如果ri＞ci、接收循环是有序的“谷-峰”值，则必须满足：ri≤ci且cr≥ri，如图8a所示。

2）如果ri＞ci、接收循环是有序的“峰-谷”值，则必须满足：rr≥ri且cr≤ci，如图8b所示。

3）如果ri＜ci、接收循环是有序的“峰-谷”值，则必须满足：ri≥ci且cr≤ri，如图8c所示。

4）如果ri＜ci、接收循环是有序的“谷-峰”值，则必须满足：rr≤ri且cr≥ci，如图8d所示。

Tecware软件已经将雨流矩阵模拟算法内置于软件中，对“from-to”形式的雨流矩阵提供了雨流编辑和雨流重构功能。将 2.2小节中得到的外推后“from-to”形式的雨流矩阵文件输入到 Tecware软件中，加载Rainflow Reconstruction模块进行时域载荷重构，重构的时域载荷谱如图9所示。对外推数据进行雨流重构后，共获得约5.11×104s的时域载荷数据。其中，x轴载荷振幅在−0.229～0.216 m/s2，y轴载荷振幅在−0.232～0.230 m/s2，z轴载荷振幅在−0.341～0.328 m/s2。

图8 雨流重构规则Fig.8 Rainflow reconstruction rules: a) ri＞ci, the receive cycle is an ordered "valley-peak" value, b) ri＞ci,the receive cycle as "peak-to-valley" value, c) ri＜ci, the receive cycle as "peak-to-valley" value,d＝ri＜ci, the receive cycle is an ordered "valley-peak" value

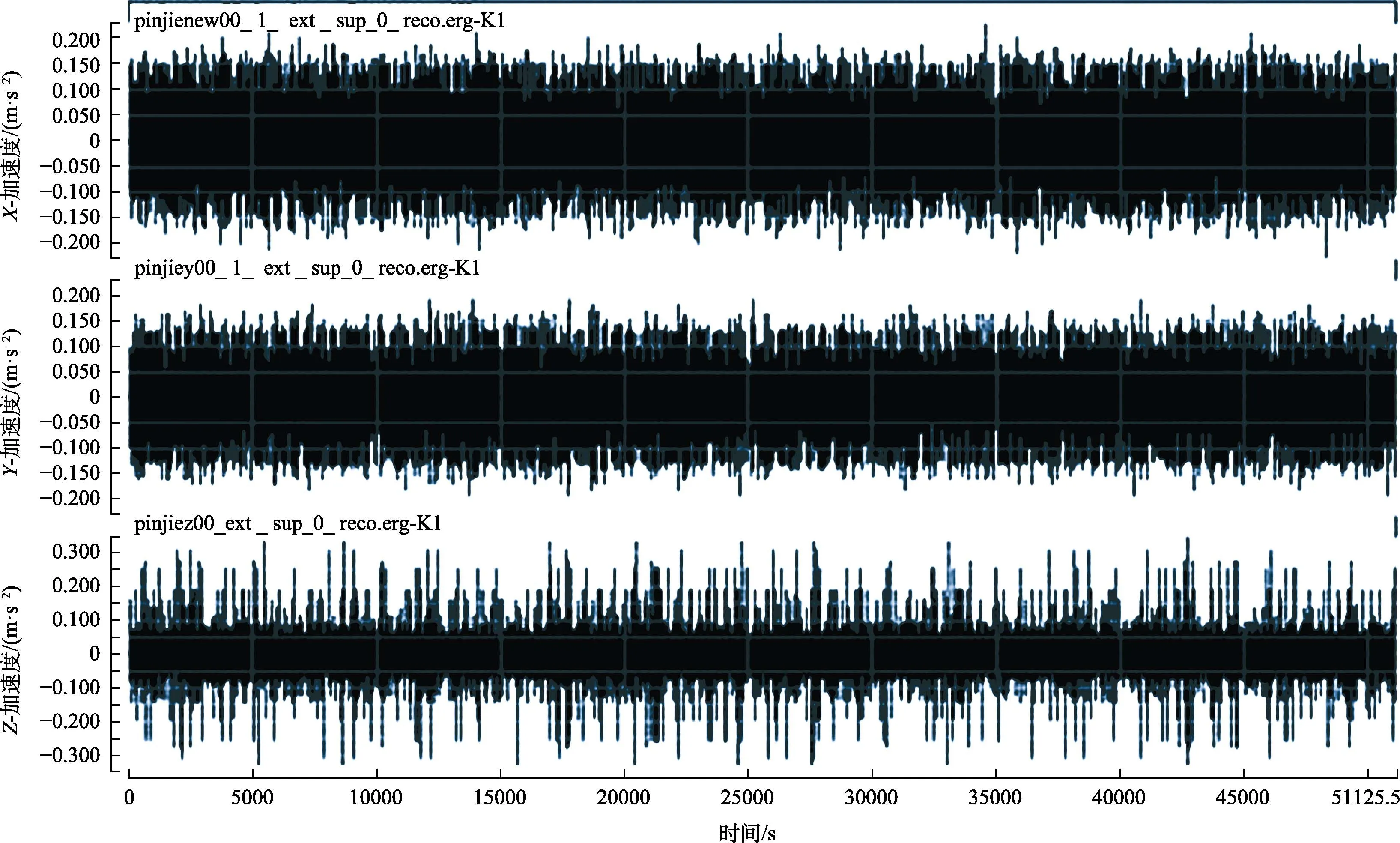
图9 外推时域载荷谱Fig.9 Extrapolated time domain load spectrum

3 有限元仿真与疲劳损伤分析

3.1 有限元仿真

依据建立的振动载荷谱，对固体发动机药柱在值班条件下的振动疲劳展开分析。进行疲劳计算时，通常需要具备三种要素：关键部位的应力幅信息、材料的疲劳性能信息以及疲劳损伤计算模型。固体发动机关键部位的应力幅可以通过有限元仿真获得；材料疲劳性能的获取通常需要开展往复拉伸试验。

首先建立某型固体发动机模型，如图10所示。模型由壳体、衬层、推进剂和人工脱粘层组成，各部件参数以及边界条件设置参照文献[7]。将载荷谱中的振动加速度数据作为边界条件输入到固体发动机模型中，依据发动机在实际值班环境下的贮存状态，对模型同时施加竖直向下的重力加速度g。有限元计算结果如图11所示，可以看出，在振动过程中，药柱内部应力较小，越靠近粘接界面，应力越大；药柱应力较为集中的部位在前后封头附近，其中，后封头附近部位的应力值最大。提取后封头附近危险点处的Mises应力幅，图12给出了部分时间段内的应力时程曲线，在该时间段内，危险点处的应力主要在0.014～0.022 MPa波动。

使用雨流计数法对危险点处的应力幅计算结果进行统计[14]，得到的统计结果如图13所示。发动机危险点处历经的循环应力载荷幅值主要集中在 0～0.001 MPa，少部分大幅值载荷分布在 0.001 MPa～0.006 MPa。

图10 固体发动机模型Fig.10 Solid rocket motor model: a) motor model,b) 1/2 motor model

图11 振动过程中药柱Mises应力分布Fig.11 Mises stress distribution of the propellant column during vibration

图12 危险点处应力时程曲线Fig.12 Stress time history curve at dangerous point

图13 雨流计数结果Fig.13 Rainflow counting result

3.2 累积疲劳损伤计算

使用雨流计数法对危险点的应力幅进行统计后，就可以进行发动机药柱的疲劳损伤计算。研究表明，Miner线性累积损伤理论以通用性较高、对随机载荷作用的材料损伤预测效果较好的优点而得到了广泛使用[15]。依据Miner线性累积疲劳损伤原理，材料的累积损伤是每个应力循环造成损伤的线性叠加，计算公式如下：

式中：D为累积损伤；Di为第i个应力循环造成的损伤；Ni为第i个应力循环幅对应的疲劳破坏次数。

文献[16]针对推进剂哑铃型试件开展了定应力往复拉伸疲劳试验，拟合得到了试验应力σ与对应的试件疲劳破坏次数N的关系式：

将式(7)代入式(6)，得到推进剂应力幅与累积损伤的关系公式：

将雨流统计结果代入式(8)，得到承受一个载荷谱周期振动的固体发动机药柱损伤值为1.059×10−4。以一个载荷谱周期的累积损伤值作为基元，计算得到发动机连续值班6个月（180 d）造成的药柱损伤（D）为0.0323。

4 结论

1）应用非参数雨流外推方法和时域载荷重构法能够有效地建立固体发动机海上值班长周期时域载荷谱，可以实现将分段监测数据中未涵盖的更加严酷的振动载荷进行量化表示，提高了载荷谱的精确性。

2）在振动过程中，药柱内部应力较小，越靠近粘接界面，应力越大；药柱应力较为集中的部位在前后封头附近，后封头附近危险点处的应力幅主要集中在0.014～0.022 MPa范围内。

3）以一个载荷谱周期的累积损伤值作为计算基元，固体发动机在海上连续值班6个月时，由振动造成的推进剂药柱累积损伤（D）为0.0323。