雨流计数法在结构疲劳损伤计算中的应用
李彬
(湖南信息职业技术学院,湖南 长沙410200)
0 引言
大型机械设备拥有更高的施工效率,能够适应巨型建筑施工的需要,可为施工企业创造更高的经济效益,倍受市场青睐。然而,大型设备成本高,所受工作载荷大,载荷状态也更加复杂,一旦发生断裂失效事故将造成巨大的经济损失以及人员伤亡,因此对结构件的疲劳损伤进行计算,并对其实施健康监测显得尤为重要。在结构的断裂事故中,疲劳断裂是最主要最危险的原因之一。所以,本文选用结构的疲劳损伤大小作为对结构健康状态进行监测的主要参数。
在工程实际中,结构的工作载荷是随着设备的工作状况与使用环境的变化而变化的,是随机载荷。随机载荷是一种不规则的动载荷、是随时间变化的载荷,在进行疲劳损伤分析时只能使用统计分析方法进行计算。由于载荷幅值和载荷循环次数是使结构件产生疲劳损伤的主要原因,所以常用计数法进行计算。计数法的种类很多,如峰值计数、雨流计数等,对于同一工况和载荷运用不同的计数方法,得到的计算结果差别可能很大。雨流计数是根据材料的应力-应变行为进行的,它得到的载荷循环和材料的应力-应变迟滞回线相一致[1],该方法能够准确地反映材料的疲劳损伤。相对其它计数方法,雨流计数法更为精确,因此被广泛运用。
1 雨流计数法的基本原理[2-3]
雨流计数法又被称为“塔顶法”在疲劳寿命计算中应用非常广泛。该方法由英国的Matsuiski和Endo两位工程师提出,他们认为材料塑性的存在是疲劳损伤的必要条件,并且应力-应变循环的滞回线(如图1)是塑性性质表现的主要形式。在计数时以一个完整的循环作为结构疲劳损伤的标志,假定大变程所引起的损伤不被小的滞回线截断所影响,将构成小滞回线的较小循环(2-3-2’和5-6-5’)从整个应变的时间历程中取出,进而得到与变幅循环载荷作用下应力-应变一致的循环计数结果。该方法在理论力学依据充分,在实践中亦能和实验结果比较接近。
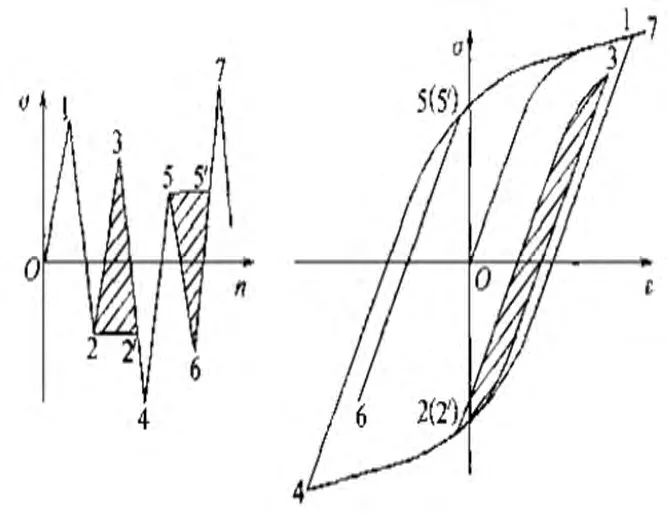
图1 应力-应变循环的滞回线
其计数规则如下(如图2):
(1)雨流在试验记录的起点和依此在每一个峰值的内边开始,亦即从1、2、3,等尖点开始。
(2)雨流在流到峰值处(即屋檐)竖直下滴,一直流到对面有一个比开始时最大值(或最小值)更正的最大值(或更负的最小值)为止(如1点流到5点就停止,2点流到4停止)。
(3)当雨流遇到来自上面屋顶留下的雨时,就停止流动,并构成一个循环(如2’)。
(4)根据雨滴流动的起点和终点,画出各个循环,将所有循环逐一取出来,并记录其峰谷值。
(5)每一雨流的水平长度可以作为该循环的幅值。
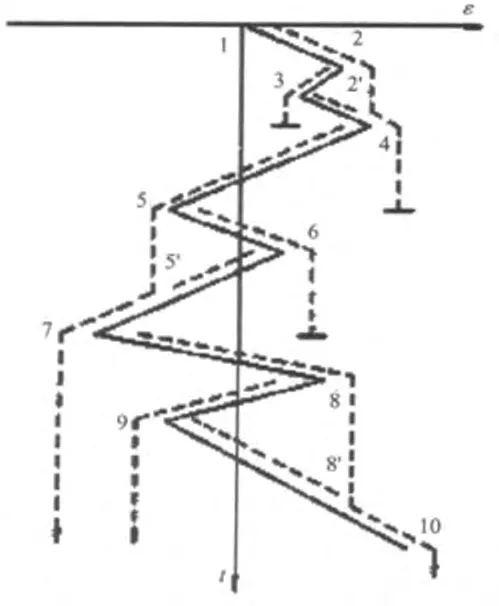
图2 雨流计数法示意图
2 雨流计数法程序的具体实现
2.1 奇异值识别准则
奇异值是指不是被测对象本身正常信号的记录,而是被传感器、变化电路以及外界电磁干扰等原因引起的异常跳点[4]。在进行雨流计数的时候,如果不剔除奇异值,会使得疲劳损伤计算结果产生很大的误差,从而对后期疲劳分析产生较大的影响。所以,在进行计数前,必须对所得的应变数据奇异值进行剔除。文章中采用3σ准则对奇异值进行剔除。计算时首先求得测量值xi的平均值,并计算残差vi=xi-x,再以采用公式(式中n为数据的个数)求得标准差σ。对数据xi,若,则该数据为奇异值,应当剔除。
2.2 峰谷值的处理
根据雨流计数的原理可知,雨流计数记录的是应变信号交替出现的循环次数,也即是“峰(谷)-谷(峰)-峰(谷)”,所以为了减少雨流计数的计算时间,必须对信号中的非峰谷值点进行识别和去除处理。文章对非峰谷值点的剔除分为两步来进行,先是剔除载荷时间历程中的连续等值点,将其合并为一个点;其次对剩下的信号点进行判别,看其是否为峰谷值点。对某个点是否为峰谷值点的判定,可以将该点与前后两点分别进行求差,并以两个差的符号是否相同作为标准来进行评判。对于非首尾点xi,如果有(xi-xi-1)(xi-xi+1)<0成立,则可认为该点为非峰谷值点,应当剔除。而对于首尾点,直接认定其为峰谷值点,就不再进行判定。
2.3 载荷时间历程的调整
如果不对载荷时间历程进行调整,直接进行雨流计数后留下的点组成的波形是一个标准的发散收敛型波形[5],这使得雨流计数无法形成完整的循环。为了避开再次雨流计数的麻烦,就必须在进行雨流计数之前先对结构载荷时间历程进行调整,从而保证处理后的信号前末端两点值为其绝对值最大值。经过时间历程调整处理后,可以保证计数过程中得到的全是完整的循环,雨流计数便可以一次性完成。
2.4 循环数的提取
本文采用的提取循环数的方法是三点法。在雨流计数循环提取时,首先依次读取三个峰谷值点,并对其进行一次计数判定后,如果符合条件,则得到一个循环,得到应力幅值与应力均值,并将该循环的末端点赋给下一次循环判定的初始点。如果不符合条件,就再向下连续读取三个点进行评判,直到最终计数全部结束。该循环提取的程序流程图设计如图3所示。

图3 提取循环程序流程图
3 疲劳损伤计算
一般通过雨流计数获取的载荷谱是三维载荷谱,这十分不利于疲劳损伤的计算。文章中采用Goodman曲线对雨流矩阵中的应力幅值以及平均应力进行等效转换,求得等效应力幅值:

式中:Se为等效应力,Su为构件的强度极限,Sa为雨流计数提取循环的应力幅值,Sm为雨流计数提取循环的应力均值。
计算各等效应力对应的频次,Palmgren-Miner(潘格伦-迈纳)线性累积损伤理论结合材料的S-N曲线计算结构的累积疲劳损伤如式(2)所示。
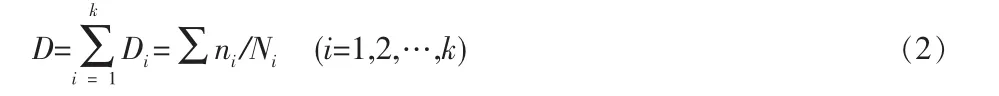
其中:ni为等效应力对应的频次,Ni为S-N曲线应力S对应下的寿命。
4 小结
本文针对结构件疲劳损伤的问题,根据雨流计数原理运用matlab软件编制了变幅循环载荷作用下应力-应变循环计数程序;并采用Goodman曲线对雨流矩阵中的应力幅值以及平均应力进行等效转换,求得等效应力幅值实现了三维载荷谱的二维化转换;最后运用Palmgren-Miner线性累积损伤理论结合材料的S-N曲线计算了结构的累积疲劳损伤,可为结构的优化设计和健康监测提供指导。
[1]王璋奇,江文强,安利强.基于雨流计数法的锅炉汽包寿命实时监测[J].热能动力工程,2007,27(1):33-37.
[2]姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2004:128-129.
[3]周家泽,管昌生.机械零件随机疲劳载荷的统计分析方法[J].襄樊职业技术学院学报,2003,2(4):4-7.
[4]肖艳军,李建勋.抗野值多速率模型及交互式状态估计[J].上海交通大学学报, 2005,39(9):1500-1504.
[5]董乐义,罗俊,程礼.雨流计数法及其在程序中的具体实现[J].计算机技术与应用,2004,24(3):38-40.

