基于改进天牛须搜索算法的自抗扰永磁同步电机控制

刘亚奇

(河南工业大学机电工程学院, 河南 郑州 450001)

群智能算法是模拟生物群体行为规律的算法,如蚁群算法[1]、粒子群优化(particle swarm optimization,PSO)算法[2]、麻雀搜索算法[3]等,用来解决复杂的优化问题。Jiang等[4]受天牛觅食和寻偶过程的启发,提出了天牛须搜索(beetle antennae search,BAS)算法。该算法结构简单,在优化过程中不依赖函数的梯度信息,因此复杂度较低,其核心代码仅有四行,具有适应能力强、寻优性能优越、易于实现和鲁棒性强的优点。BAS算法一经提出就受到了广泛的关注,同时对BAS算法的改进也是很热门的研究方向。Song等[5]把BAS算法和PSO算法结合起来,用天牛位置更新公式更新粒子的速度和位置,将天牛须搜索应用到群体搜索机制中,在无线传感器的应用中取得了比标准PSO算法更好的效果。徐鑫等[6]提出了一种引入精英个体和包围机制的改进BAS算法,首先利用包围机制减少参数,自适应地更新步长,然后用精英个体使得算法跳出局部最优解。实验表明该算法收敛速度快,同时避免了算法陷入局部最优。

自抗扰控制器(active disturbance rejection control,ADRC)[7]是韩京清研究员于1998年正式提出的,其核心思想是将系统中的不确定性、模型误差和干扰作为一个扩张状态,通过扩张状态观测器进行估计补偿。该控制器不依赖被控对象的模型,具有很好的工程应用前景。基于智能优化算法的参数优化方法,占据了非线性ADRC参数整定的半壁江山。童成意[8]设计了一种基于免疫粒子群算法自整定参数的ADRC,该算法在粒子群算法的基础上,引入了人工免疫系统中的克隆选择机制和免疫网络思想,并将其成功应用于混沌系统控制,取得较好的控制效果。易星等[9]提出了一种双种群混沌鲸鱼算法对ADRC的参数进行整定,该算法应用混沌策略和双种群协同机制来解决鲸鱼算法在迭代后期寻优速度缓慢的问题,实验结果表明改进后的控制器具有良好的抗扰能力。

本文提出了一种基于量子进化的天牛须搜索(QBAS)算法,用来解决传统的BAS算法容易陷入局部最优、迭代速度慢的问题,并将改进后的天牛须搜索算法用于ADRC参数的在线整定,最后用基于混合算法的ADRC来控制永磁同步电机,进行仿真实验。

1 自抗扰控制

1.1 数学模型

ADRC由跟踪微分器(tracking differentiator,TD)、扩张状态观测器(extended state observer,ESO)和非线性反馈控制率(nonlinear state error feedback control law, NLSEF)3部分组成,其结构如图1所示。

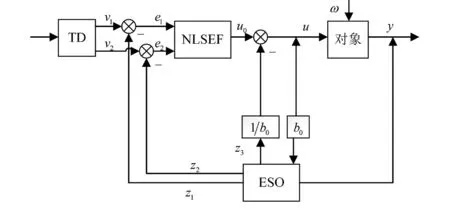
图1 自抗扰控制器结构图

下面以一个二阶系统作为研究对象来搭建ADRC:

(1)

TD的作用是对输入的指令信号v安排过渡过程,目的是平衡系统响应速度和系统超调的矛盾,提高系统的鲁棒性,增强系统的稳定性。TD的数学表达式为:

(2)

式中:v1(k)、v2(k)为TD的输出信号,k为采样时刻,h为采样周期,r为速度因子,h0为滤波因子,fst()为非线性误差函数。

(3)

式中:a和d为中间变量,sign()为符号函数。

(4)

ESO是先将总扰动扩张成系统的一个新的状态变量,然后利用系统的输入输出观测出所有的状态(包括原有状态变量和扰动的状态变量)。ESO的数学表达式为:

(5)

式中:e0(k)为误差信号,z1、z2和z3为跟踪信号,β01、β02、β03、a1、a2、a3和δ1均为控制器参数。

NLSEF可以利用TD的输出信号v1和v2与扩张状态观测器各状态变量估计值相减,得到误差量e1和e2,然后对扰动进行补偿。NLSEF的数学表达式为:

(6)

式中:β1、β2为控制器的增益系数,u0(k)为NLSEF的控制信号,a4、a5和δ2均为控制器参数。

其中fal(e,a,δ)为非线性函数:

(7)

式中:e代指e1、e2,δ代指δ1、δ2。

1.2 参数分析

大量的工程实践证明,一个控制器性能的好坏取决于其参数的调整是否合适。ADRC的参数众多,如果全部用智能优化算法整定比较困难,所以在一些参数已设定好的基础上在线整定其他参数可以取得不错的效果。在ADRC中,TD的参数整定有一定的独立性,其中滤波因子h0一般取3h～10h,速度因子r决定了跟踪速度的快慢,可以根据系统的响应速度自主调节。在ESO中,z1、z2和z3为跟踪信号,其中z1和z2是对状态变量的估计,z3是对扰动变量的实时估计,式(5)、(6)中控制器参数0≤ai≤1(i=1,2,…,5),取a1=1.00、a2=0.25、a3=0.25、a4=0.75、a5=0.50[10],β01、β02、β03为可变参数,是需要调试的,其直接影响ESO的观测性。对于NLSEF,影响其性能的是非线性配置系数β1、β2,其作用与PID控制器中的比例系数和积分系数类似,需要调试才能满足要求。因此,设计控制器时除了β01、β02、β03、β1和β2参数需要调试外,其他参数都可以设置成固定值,这5个参数很大程度上影响了ADRC的控制性能,本文用一种改进的天牛须搜索算法在线自整定这5个参数,设计了一种基于混合算法的自抗扰控制器。

2 改进天牛须搜索算法

2.1 BAS算法数学模型

在D维空间中,天牛左右须的位置x1、xr表示为

x1=xt+dtb

xr=xt-dtb

(8)

式中:xt为天牛在第t次迭代时的位置,t为迭代次数,dt为天牛两须之间的距离,b表示天牛的随机朝向。

(9)

式中:rand()为随机函数。

根据两侧触须的气味浓度,更新天牛的位置:

xt+1=xt+λtbsign(f(xr)-f(x1))

(10)

式中:λt为步长,f()为适应度函数。

更新下一步的搜索范围和步长:

λt+1=λt·eta

(11)

dt+1=dt·eta+0.01

(12)

式中:eta为两须距离和步长的衰减系数,通常取0.95。

2.2 QBAS算法数学模型

Han等[11]将量子遗传算法(quantum inspired genetic algorithm,QIGA)扩展为量子进化算法(quantum inspired evolutionary algorithm,QEA),QEA是基于量子比特和量子力学态叠加的概念提出来的。QEA用量子位编码(real coded quantum,RCQ)表示染色体,在算法后期用量子旋转门(the quantum rotation gate,QRG)完成更新。Chen等[12]设计了一种基于量子进化的鸽群算法,经实验验证,该算法具有优越的寻优性能。

n个量子位的染色体形式表示如下:

(13)

本文中当前最优解被认为是“0”态和“1”态的线性叠加,最优解的量子由RCQ表示为:

(14)

式中:xbest,n为当前最优解,αn为两种状态线性概率。

此时天牛的收敛方向重新被观测后定义为xbest,i,表达式为:

(15)

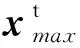
在量子力学中,量子态可以用波函数ω(xi,t)表示。波函数的平方|ω(xi,t)|2称为概率密度,表示量子态在对应时间和位置出现的概率。式(15)表示当前RCQ的观测值,可以用概率密度求得,概率密度的表达式为:

i=1,2,3,…,n

(16)

式中:μi为期望值,用当前最优解表示。σi定义为:

(17)

式中:αi为两种状态线性概率。

在QEA中,由于量子位下的染色体不是单一状态,不能进行传统的选择、交叉、变异等操作,所以本文采用QRG作用于量子位上,使其状态位发生变化,进而改变线性概率αi的分布域。对于有n个量子位的个体,第i个量子位的更新情况如下:

(18)

3 控制器设计与实验仿真

3.1 适应度函数的选取

本文选取时间绝对误差积分准则(integral of time and absolute error, ITAE)作为适应度函数,该准则是描述系统的期望和实际输出之间偏差的一种准则,按此标准设计的控制器,对误差的抑制能力强,振荡小,是衡量控制器控制性能的一个常用标准,同时为了抑制超调对系统的影响,将系统的超调量也作为评价指标加入适应度函数中[13]:

(19)

式中:JITAE为适应度函数;e(t)为误差;σ为系统超调量;ω1和ω2为权值,根据调试经验选择ω1=ω2=10。由于适应度函数始终存在最小值,优化算法取得的值越接近最小值,代表整定参数的ADRC的效果越好,所以此时ADRC的参数整定问题简化成了一个高维函数求最小值的问题。本文设计的基于改进天牛须搜索算法的自抗扰控制器(QBAS-ADRC)结构如图2所示。

图2 QBAS-ADRC结构

为了验证QBAS-ADRC的性能,在Simulink中搭建基于混合算法的ADRC模型,同时引入一个频率和幅值为1的正弦信号作为扰动来模拟仿真,把QBAS-ADRC与BAS-ADRC和PSO-ADRC的控制输出结果作为对比。PSO算法的学习因子设置为c1=c2=1.5,惯性权重ω*为0.8,BAS算法的步长衰减系数eta为0.95,步长λ为10。另外设置β01、β02的取值范围均为[0,200],β03的取值范围为[0,4 000],β1的取值范围为[0,500],β2的取值范围为[0,200],b0设置为1,r设置为1,h0设置为0.01,选取一个二阶被控对象:

3.1.1 搭育苗棚 早春茬（在日光温室中）和秋延茬（在空闲地）都要搭小拱棚，棚宽2 m左右，长度根据育苗数量而定。苗床要求平整，宽1.5 m左右，有利于摆放穴盘或营养钵。苗床四周起土埂10～15 cm，以利于蓄水保墒。

(20)

适应度函数迭代图如图3所示,由图可知, QBAS具有更快的寻优速度,在运算过程中用量子位更新当前最优解,使得算法在陷入局部最优解时能够很快地跳出来,并能很好地感知算法的欺骗性。

阶跃响应曲线如图4所示,由图可知,基于混合算法的ADRC具有更快的响应速度和更优的抗扰性能。

3.2 PMSM仿真实验

为了进一步验证基于QBAS-ADRC的控制性能,本文设计了永磁同步电机(PMSM)的控制实验。PMSM具有非线性、多变量、强耦合的特点,现对其进行简化分析。PMSM的电磁转矩Te方程为:

(21)

式中:np为磁极对数,ψf为转子磁链,Ld和Lq分别为d轴和q轴的电感,iq和id分别为d轴和q轴的电流。

PMSM的运动方程为:

(22)

式中:J为转动惯量,TL为负载转矩,B为黏滞摩擦系数,ωr为电机转子的角速度。

在同步旋转坐标系下,采取id=0控制策略时,PMSM位置环的数学模型如下:

(23)

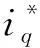
(24)

将系统的内外扰动总和扩张成新的状态变量x3,并记x3=ξ,则可以将系统扩张成如下控制系统:

(25)

根据以上的数学模型,在Simulink分别搭建混合PSO 算法和混合QBAS算法的PMSM的ADRC控制模型,如图5所示。

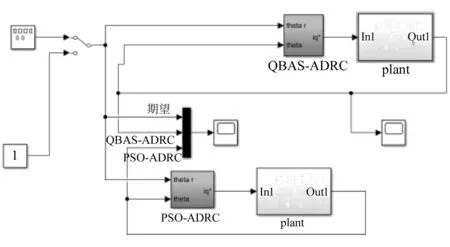
图5 PMSM的ADRC控制模型

实验选取的PMSM的参数见表1。

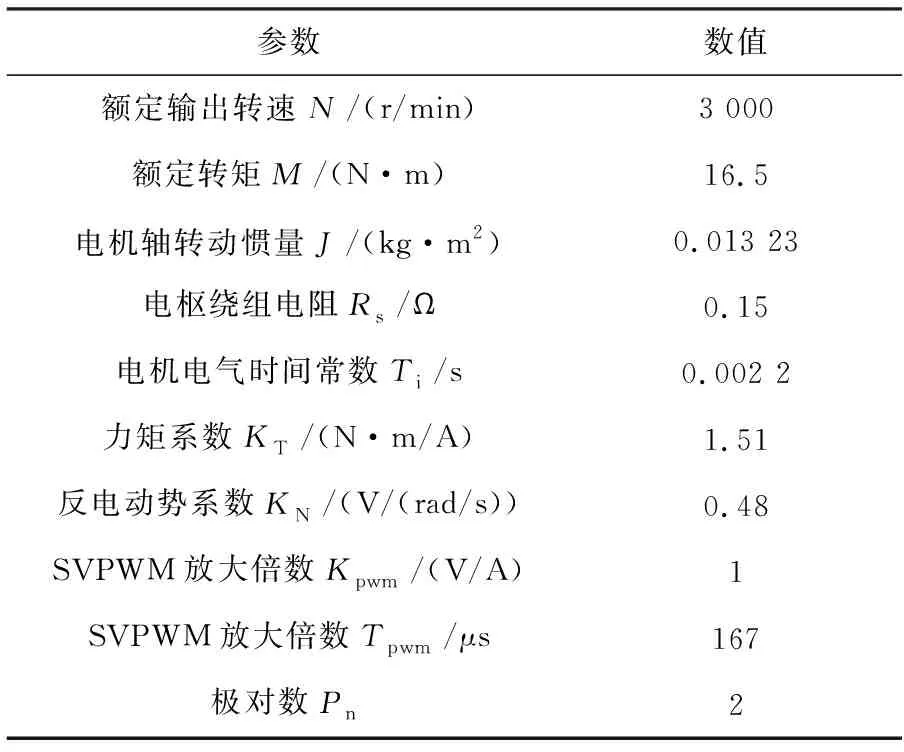
表1 PMSM参数

以PMSM为被控对象,通过QBAS算法和PSO算法在线自整定的ADRC的控制器参数见表2。

在确定被控对象的前提下,为了防止输出的信号受到输入波形的影响,本文选取单位信号、方波信号和正弦信号作为信号源,其跟踪输出结果如图6～图8所示。

图6 跟踪单位阶跃信号仿真结果

图7 跟踪方波信号仿真结果

图8 跟踪正弦波信号仿真结果

由仿真结果可知,QBAS对自抗扰控制器参数进行在线自整定的方法可行有效。对于不同的输入信号,都具备良好的适应能力。与PSO算法相比,QBAS算法进行参数优化时,控制器跟踪的上升时间和达到稳态的时间都比较短,并且超调量比较小,有效解决了超调量与快速性之间的矛盾,满足工程实际的要求,具有一定的工程应用价值。

4 结束语

针对ADRC参数整定困难的问题,本文提出了一种基于量子进化的天牛须搜索算法来在线整定ADRC的参数。针对天牛须搜索算法在迭代后期速度慢、易陷入局部最优的问题,把算法寻优过程中获得的当前最优候选解认为是正、伪两种状态的量子位线性叠加,用实数编码的量子重新表示,然后利用量子旋转门更新量子表达式,增加了当前最优解的多样性,并能很好地感知算法的欺骗性。采用PMSM进行仿真验证,与POS算法整定ADRC仿真结果相比,基于量子进化的天牛须搜索算法整定的ADRC具有良好的抗扰性能和更快的响应速度。