蝴蝶定理在高考试题中的应用——2022全国甲卷理科第20题背景探幽

林健航

⦿ 江西省九江市教育科学研究所

1 试题呈现

例(2022全国甲卷·20)设抛物线C:y2=2px(p>0)的焦点为F,点D(p,0),过点F的直线交C于M,N两点.当直线MD垂直于x轴时,|MF|=3.

(1)求C的方程;

(2)设直线MD,ND与C的另一个交点分别为A,B,记直线MN,AB的倾斜角分别为α,β.当α-β取得最大值时,求直线AB的方程.

解法1：(1)抛物线C的方程为y2=4x.(过程略.)

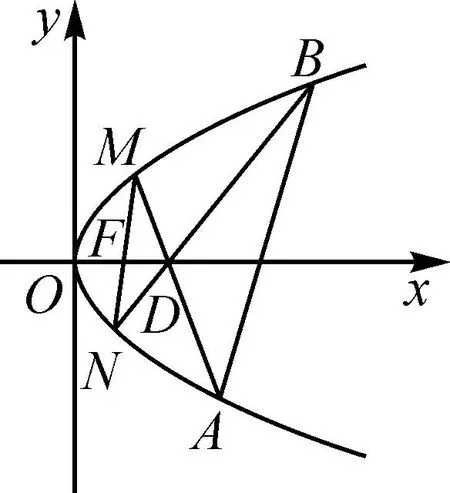
图1

(2)如图1,设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4).

由抛物线的对称性知,当α=90°时,β=90°,则α-β=0.

当α≠90°时,β≠90°,设过点(x0,0)的直线方程为x=my+x0.

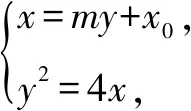
当x0=1时,得y1y2=-4;

当x0=2时,得y1y3=-8,y2y4=-8.

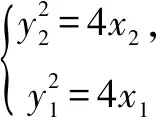
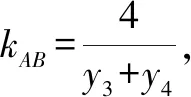
当α∈(0°,90°)时,β∈(0°,90°),且α>β.

当α∈(90°,180°)时,β∈(90°,180°),且α<β.

故要使α-β最大,则α∈(0°,90°).

设kAB=k>0,则kMN=2k.

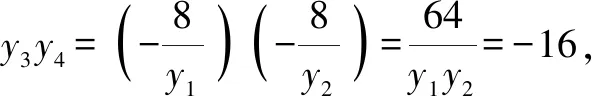
此解法为通性通法.本题主要考查抛物线的定义、直线与抛物线的位置关系、直线的倾斜角和斜率的概念、均值不等式等基础知识,考查数形结合、分类讨论和点差法等数学思想方法,考查逻辑推理、直观想象、数学运算等核心素养.

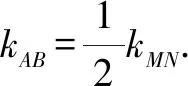
2 背景探幽

本题的背景就是坎迪定理,下面我们先从蝴蝶定理入手进行探究.

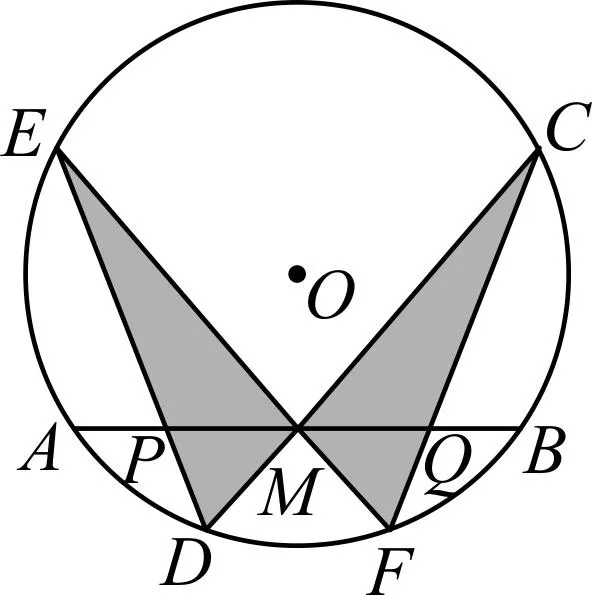
图2

如图2,设M是圆O中弦AB的中点,过点M任作两条弦CD,EF,连接DE,CF,分别交AB于P,Q两点,则MP=MQ.

这个问题的图形,像一只在圆中翩翩起舞的蝴蝶,这正是该结论被冠以“蝴蝶定理”美名的缘故.

此定理的证明方法很多,下面用中学的有关知识给出该定理的两种证法.

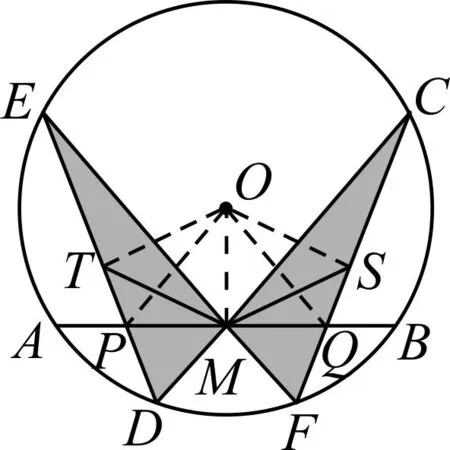
图3

证法1：(初中几何知识)如图3,过圆心O作CF,ED的垂线,垂足分别为S,T,连接OM,OP,OQ.

因为∠OSQ=∠OMQ=90°,所以O,S,Q,M四点共圆.

于是∠QSM=∠QOM.

同理可得∠PTM=∠POM.

又∠F=∠D,易得△FSM∽△DTM,于是有∠QSM=∠PTM,所以∠QOM=∠POM,

又OM⊥PQ,所以MP=MQ.

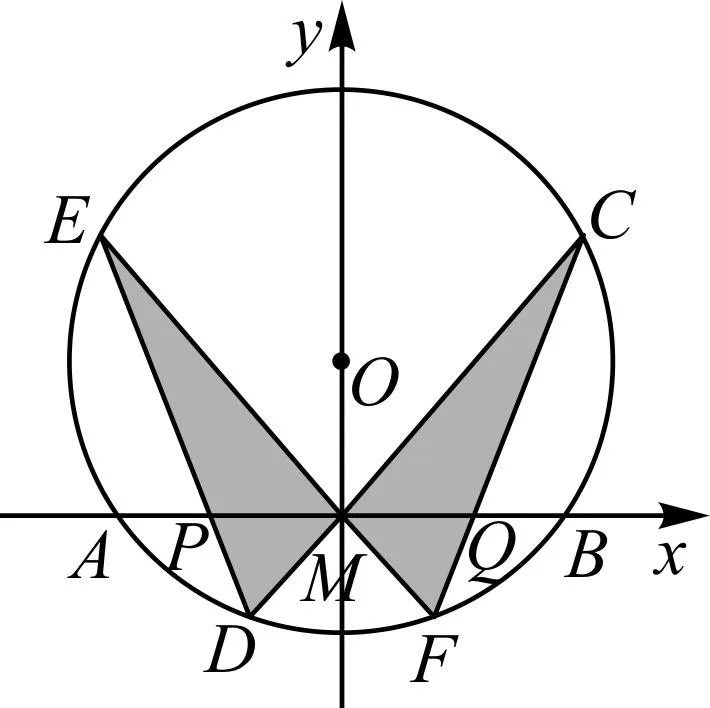
图4

证法2：(高中几何知识)如图4,以M为坐标原点,AB所在的直线为x轴,建立平面直角坐标系.设OM=b,则圆O的方程可写为

x2+y2-2by+c=0.

①

设直线CD,EF的方程分别为y=k1x,y=k2x,合并为

(y-k1x)(y-k2x)=0.

②

于是,过曲线①②的交点C,D,E,F的二次曲线系方程为

x2+y2-2by+c+λ(y-k1x)(y-k2x)=0.

③

③式中令y=0,可知曲线③与AB的交点P,Q的横坐标满足(1+λk1k2)x2+c=0.由韦达定理,可得xP+xQ=0,即|MP|=|MQ|.

由仿射几何知识可知,蝴蝶定理在圆锥曲线中也成立:

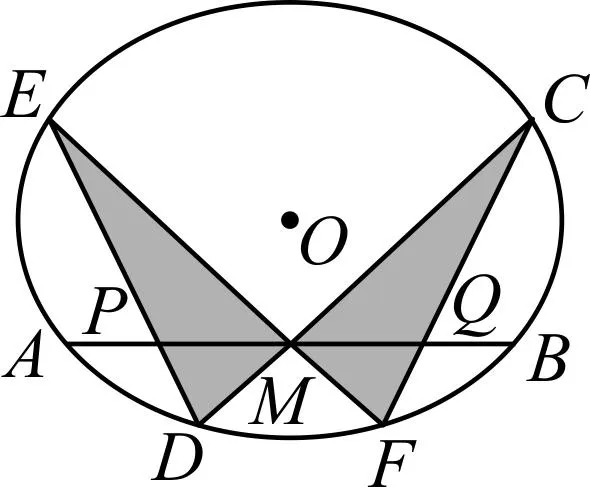
图5

如图5,在圆锥曲线中,过弦AB的中点M任作两条弦CD和EF,直线DE,CF交直线AB于P,Q两点,则MP=MQ.(证明略)

若将M改为弦AB上的任意一点,则可得到坎迪定理:

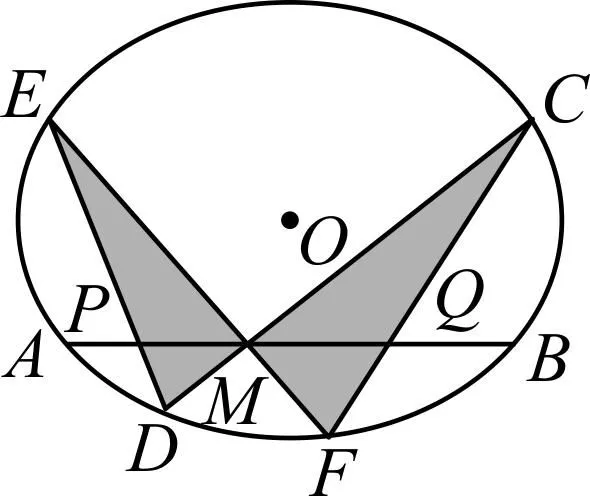
图6

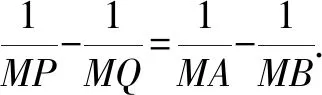
由蝴蝶定理和坎迪定理,可得上述例题的简单解法.

解法2：(1)略.

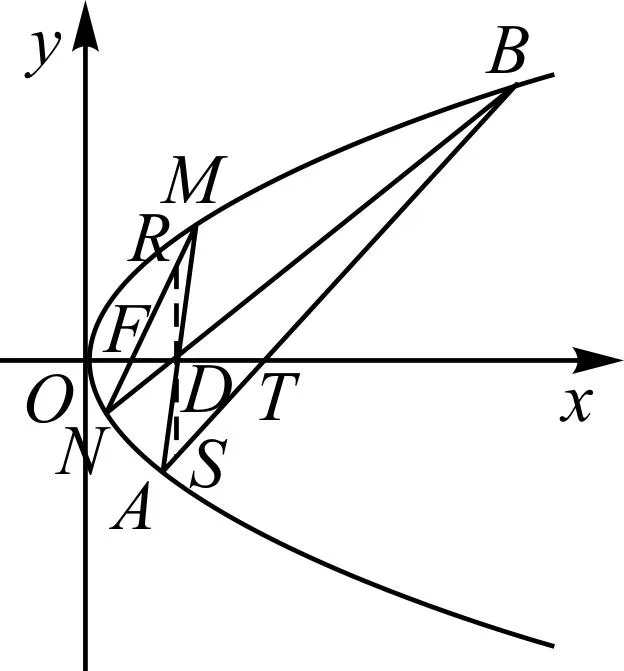
图7

解得xT=4,即直线AB经过点T(4,0).

由解法1知,要使得α-β取得最大值,则kAB=k>0.过点D作x轴的垂线分别交MN,AB于点R,S.

3 应用拓展

若将上述例题一般化可得下列两个结论.

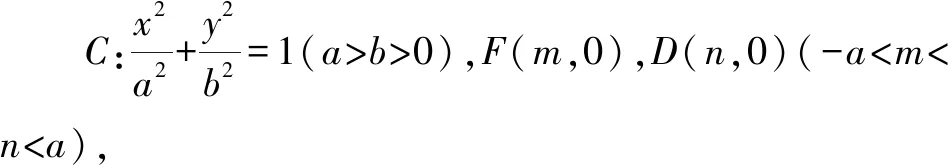
研究解析几何问题,不仅要研究其解法,还要研究其几何背景,扣住几何属性,在更广、更深的层面上认识试题,发挥其教学功能,于教学过程中落实学科素养.Z