亲历问题解决过程 品悟一一列举策略——《解决问题的策略》教学设计

文|秦宏霞

【教学内容】

苏教版五年级上册第94、95页例1 及随后的练一练，练习十七第1～4 题。

【教学过程】

一、温故知新，复习导入

师：同学们回忆一下，我们已经学习过哪些解决问题的策略？

引入：从三年级开始，已经学习过从条件想起、从问题想起、列表、画图等策略。

指出：这些策略可以帮助我们分析题意，理清数量关系，更好地解决实际问题。

揭题：今天，老师将和大家一起探究一种新的策略。（板书：解决问题的策略）

二、探究解题，认识策略

1.理解题意，明确方法

出示例1：王大叔用22 根1米长的木条围一个长方形花圃，怎样围面积最大？

师：大家轻轻地读一读，你知道了哪些信息？同桌交流。

提问：你是怎样理解“22 根1米长”这句话的？围成的是什么形状？

引导：根据题中的条件和问题，你能想到些什么？（围成长方形的长和宽不能是小数）

指出：用22 根1 米长的木条围成长方形，说明长方形的周长是22 米，长和宽都是整米数（板书：周长22 米）；周长的一半是11米，也就是根据长加宽的和是11米（板书：长+宽=11 米），列举出不同围法的长方形，再找出面积最大的围法。

2.自主探究，感悟策略

师：我们能不能试着帮王大叔围一个长方形花圃？你打算怎么围？

请大家拿出《学习单（一）》，先尝试解决，再小组交流。

学生列举，教师巡视，相机指导。

交流：你通过列举，围成了哪些长和宽都不同的长方形？找到面积最大的围法了吗？（选择学生中几种具有代表性的列举结果，呈现交流）

（1）画图列举

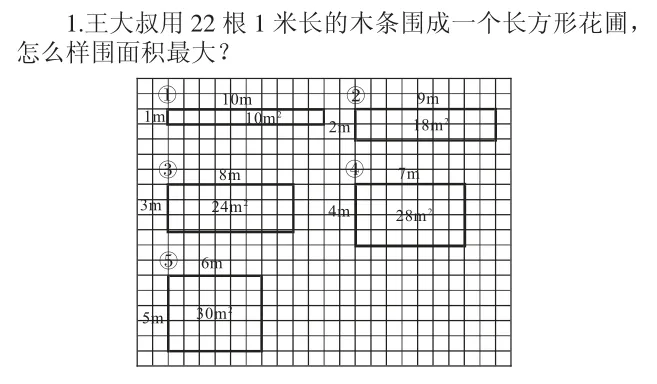
（2）列表列举

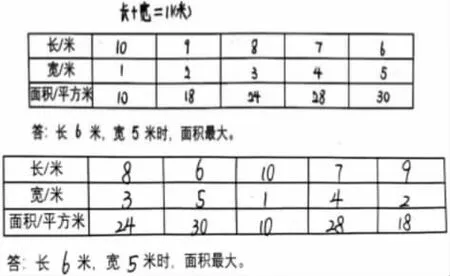
3.算式列举

师：同学们所用的方法不同，观察这些方法有什么共同的地方？说一说，使用了什么策略？

指出：我们把这种从大到小或从小到大一一排列出来的策略叫作“一一列举”的策略。（板书：一一列举）

提问：对上面几位同学的做法，你有哪些好的建议？（指出其中一位同学列举有些凌乱，没有按顺序）

小结：在一个一个列举时，可以从长10 米、宽1 米起，有顺序地一个一个列举出不同的围法，到长6 米、宽5 米时为止。这样就能做到不遗漏、不重复。（板书：有序列举——不遗漏 不重复）

追问：有序列举有什么好处？为什么列举到长6 米、宽5 米时为止？

3.观察比较，探寻规律

指出：周长相等的长方形，面积不一定相等，当长方形周长一定时，长和宽越接近，面积越大。

师：真了不起！通过一一列举的策略，同学们不仅解决了问题，还发现了规律。

三、回顾反思，内化策略

师：请同学们回顾一下，我们是怎样帮王大叔解决问题的，运用了什么策略？

师：我们曾经遇到哪些问题需要把所有情况一一列出来？

举例：如10 以内数的组成（一年级上）、编关于几的乘法口诀（二年级上）、3 张数字卡片可以组成多少个不同的三位数（二年级下）等等。

指出：这里都是我们曾经用过的一一列举的例子，现在可以像例题那样先列表再按序列举，这样能使列举的过程更清楚、更准确。

四、拓展应用，巩固策略

1.观看表演

王大叔的农场里有一个神奇的音乐钟，在音乐响起的时候记录一些数据。出示问题：

（1）指名读题。提问：请同学们想一想，然后列一列，找到问题的答案。

（2）讨论交流，（两名学生展示作业纸，一对一错）明确13:00和15:40 这两个时刻会发出铃声。

追问：列举到15：40 之后还要列举吗？

生：不需要，因为题目只要求到16：00。

2.不知不觉时间到了中午，王大叔给大家带来了丰盛的午餐。

出示“今日供应”，问题：

（1）提问：你能找出所有的搭配方式吗？

（2）学生独立完成，然后交流反馈。

追问：第四位同学的方法你理解吗？学生介绍连线法，用乘法3×4＝12（种）来计算。

3.拓展题

出示题目：爸爸妈妈和小华三人要在农场里照相，有多少种不同的照法？（调换顺序算一种）

师：你们打算用什么策略解决这个问题？

生：一一列举。

师：列举时，打算分哪几种照相的情况？

生：分三类：单人照，双人照，三人照。

师：和哪题有点相似，用自己喜欢的列举方式进行吧！（两名学生说说做法）

师：你是怎样列举的？

师：一共有几种不同的情况？

（一共有7 种）

师：如果他们站在一条直线上，考虑不同的位置，一共有多少种呢？四人小组讨论汇报，全班交流。（一共15 种）

4.学生独立完成“练习十七”第1～4 题

学生评讲、纠错，说解题的思路，教师相机指导。

五、总结延伸，提升策略

提问：我们随着小华和爸爸妈妈在农场里参观活动，你有哪些收获呢？

小结：通过这节课的学习，我们又认识了一种新的解决问题的策略“一一列举”，随着你们知识的增长，将来一定会发现更多、更妙的解决问题的策略。