磨粒流加工壁面效应研究

汤炉滨　文东辉　孔凡志　袁巧玲

摘要：数值模拟了圆柱内表面的初始粗糙度、入口流速和内孔直径对壁面流场压力、局部压差及剪切力的影响规律，分析了入口处流场速度和剪切力的形成过程，从磨粒切削作用角度剖析了圆柱内表面入口处过抛现象的形成原因，结合磨粒流加工试验揭示了各参数对壁面效应的影响规律。理论分析和试验结果表明：增大圆孔直径或减小入口流速能有效改善磨粒流流场压力的均匀性，初始表面粗糙度对流场压力数值及其局部压差有微弱影响；入口处圆孔壁面速度突变引起剪切力突变，从而导致磨粒流加工过抛现象；初始表面粗糙度Ra=0.296 μm时有利于减弱磨粒流加工的壁面效应，而Ra=4.273 μm时有利于提高材料去除速率。

关键词：流场压力；剪切力；壁面效应；过抛现象

中图分类号：TG580

DOI：10.3969/j.issn.1004-132X.2023.09.008

Research on Wall Effect of Abrasive Flow Machining

TANG Lubin1，2 WEN Donghui1，2 KONG Fanzhi1，2 YUAN Qiaoling1，2

Abstract： Effects of initial surface roughness， inlet flow velocity and hole diameter on flow field pressure， local pressure difference and shear force of cylinder inner wall were simulated by numerical method. Formation processes of flow field velocity and shear force at the cylinder entrance were detected， then over-polishing phenomenon accrued at the entrance of cylinder inner surfaces was deduced according to the abrasive forces action. Effects of all parameters on wall effect during abrasive flow machining was revealed by abrasive flow machining experiments and simulation. Theoretical analysis and experimental results show that， increasing diameter of round hole or reducing inlet flow rate may improve pressure uniformity of abrasive flow field effectively， initial surface roughness has a weak effect on flow field pressure value and the local pressure difference. Sharp transition of wall surface velocity at the entrance causes a sudden change of shear force， then leads to over-polishing phenomenon of abrasive flow machining. Initial surface roughness Ra=0.296 μm is conducive to weakening wall effect of abrasive flow machining and Ra=4.273 μm is conducive to increasing material removal rate.

Key words： flow field pressure; shear force; wall effect; over-polishing phenomenon

0 引言

航空航天、國防武器及汽车工业等对大长径比微孔精密零件的需求日益增长，此类零件的抛光加工难度较大［1］，磨粒流加工（abrasive flow machining，AFM）是一种能适应大长径比复杂微孔流道的抛光技术［2-4］。然而，磨粒流加工过程存在较为显著的壁面效应，即工件表面粗糙度和表面形貌的差异以及入口处的过抛现象导致加工后表面质量一致性较差，因此，调控磨粒流流场均匀分布是抑制壁面效应的关键因素，而磨粒流流场特性受入口压力和流速、磨料浓度、磨粒粒径、流动形态、工件初始粗糙度等因素的影响。

BARAIYA等［5］研究磨粒粒径、磨料浓度、循环次数等对表面粗糙度的影响后发现：表面粗糙度的改善率随循环次数和磨料浓度的增加而增加，随磨粒粒径的减小而减小，表面粗糙度最大降幅为37.89%。李俊烨等［6］研究磨粒流入口压力对壁面压力的影响来揭示其表面创成机理，发现入口压力越大，异型曲面的表面粗糙度Ra越小，且压力与速度的不匹配导致出现磨粒流漩涡现象。李琛等［7］数值模拟了流场压力和速度流场的分布，经过20 h加工后，工件入口处与出口处粗糙度分别降至312 nm和566 nm。SINGH等［8］研究初始粗糙度为0.50～0.67 μm时不锈钢316L的抛光效果，发现磨粒流加工后最佳表面粗糙度降至48 nm，降幅为92.2%。AZAMI等［9］提出了一种旋转磨粒流加工方法，分析了磨粒粒径和旋转速度对表面粗糙度的影响，表面粗糙度可从微米级降低至纳米级。SHARMA等［10］通过施加不同频率的超声波来改变磨粒流态，进而减小表面粗糙度，当施加频率为20 kHZ时，表面粗糙度最大降幅为81.02%。WANG等［11］开发不同黏度的磨料，发现黏度较高的磨料加工工件后，其表面均匀性提高了58%。

已有研究多聚焦于各参数与表面质量、加工效率等加工特性的定性联系，鲜有对流场压力与剪切力分布规律的深入报道，以及对入口处过抛现象的成因剖析和壁面效应作用规律的阐述。本文以某航天零件上的圆柱内表面为研究对象，模拟了初始表面粗糙度、入口流速、圆孔直径对磨粒流场压力及剪切力的影响规律，阐明了不同参数对壁面效应的作用规律。

1 磨粒流场特性分析

1.1 磨粒流加工原理

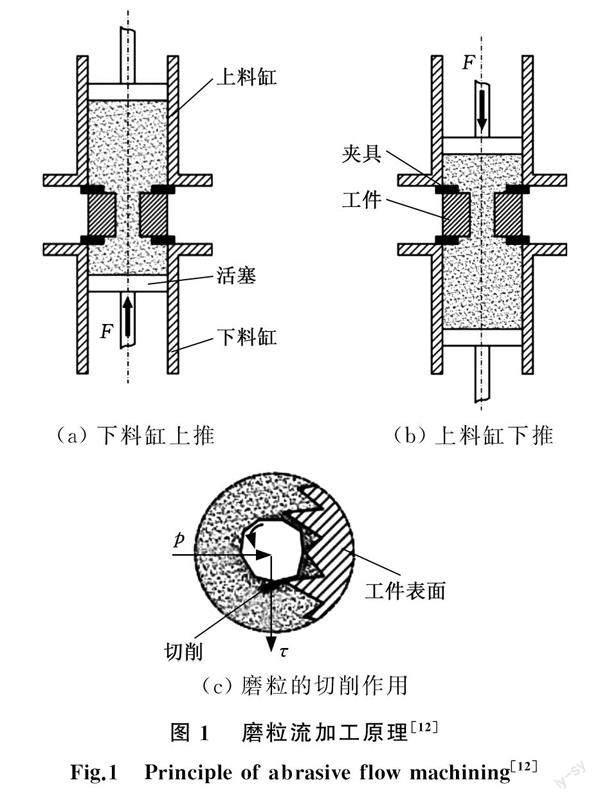
磨粒流加工原理如图1所示。磨料装入下料缸，将工件及夹具夹持在上下料缸之间，上下料缸、工件及夹具之间构成密闭空间。通过液压力F推动上下料缸活塞，进而挤压磨料使其往复切削加工工件的待加工面。

1.2 材料去除函数

计算流体动力学CFD中SST k-ω模型结合了k-ε和k-ω模型，适用于低雷诺数的湍流模型在壁面区域的模拟，在此情形下使用该模型具有更高的计算精度。SST k-ω模型表达式如下［13］：

式中，C1为常数。

1.3 粗糙表面的壁面特性

计时鸣等［17］将不同粗糙程度的圆柱内表面分为粗糙区、光滑区和过渡区，分类依据与黏性底层厚度δ′和粗糙厚度Δ有关。当δ′＞Δ时，粗糙厚度对湍流核心几乎没有影响，称为光滑区；当δ′＜Δ时，粗糙厚度会加剧湍流程度，增大能量耗散，称为粗糙区。两种作用方式见图2，而过渡区则介于两个区域之间。

不同区域的摩擦力差异较大，进而对磨粒的流动形态产生影响。过渡区摩擦因数的计算公式为

（9）

式中，λ为摩擦因数；d为磨粒粒径；r0为流道半径；Re为雷诺数。

当d→0时，由下式得到光滑区的摩擦因数：

（10）

在粗糙区，粗糙凸面完全暴露在湍流核心，不依赖雷诺数，则摩擦因数计算公式为

（11）

2 磨粒流加工的数值模拟

2.1 几何模型

图3a为“夹具-工件”爆炸图，采用抛光、镗孔、铰孔、线切割四种工艺方法加工出不同初始表面粗糙度的圆柱内表面，圆孔长L=200 mm，通过螺母和螺杆将工件和夹具固定，磨料在孔内的流动方向如图3a中箭头所示。图3b为“夹具-工件”俯视图，粗实线为所需要抛光的表面，阴影部分为磨料通道。由于上下料缸的往复加工参数相同，故仅对上料缸下推单向过程的磨粒流场特性进行仿真分析。利用SolidWorks软件建立流场的几何模型，如图4a所示，包括料缸段、夹具段和圆孔段三部分；为保证数值模拟结果的收敛性与准确性，通过SolidWorks对几何模型进行分割处理，再利用Workbench-Meshing对几何模型进行网格分块划分，如图4b所示。划分后的网格类型为六面体，圆孔段的网格单元数为133 800，网格节点数为139 695。

2.2 參数设置

选择多相流模型为Mixture，开启能量方程，采用速度入口和压力出口，主相设置为聚合物，动力黏度0.15 Pa·s，密度ρ0=1340 kg/m3;第二相设置为SiC颗粒，磨粒粒径d=38 μm，磨料浓度η0=10%，环境温度T0=293 K。壁面处采用无滑移边界条件并设置其为对流换热表面，以模拟暴露在空气中的自然对流换热，对流传热系数δ0=20 W/（m2·K）。采用抛光、镗孔、铰孔、线切割等四种工艺加工出不同初始表面粗糙度的圆孔，经吉泰TR200表面粗糙度仪测得壁面的初始表面粗糙度Ra依次为0.296 μm、1.820 μm、3.181 μm、4.273 μm。由式（8）可知，材料去除量与流场压力和剪切力直接相关，而压力和剪切力又与初始表面粗糙度Ra、圆孔直径D0、入口速度vin相关，因此，以初始表面粗糙度、圆孔直径、入口流速三个参数为变量进行数值模拟，分析各参数对圆孔壁面压力及剪切力的影响规律。各参数水平及其数值见表1。

2.3 网格可靠性验证

数值模拟时网格数量会影响计算结果的精度，故需要验证网格数量与计算结果之间的无关联性。本文以圆孔壁面为研究对象，即此处主要针对圆孔段的网格进行无关性验证，得到三种不同网格数量下圆孔壁面不同位置处的无关性检验结果。由此可见：当网格数量由52 520增至133 800时，最大压力变化率为9.060%；当网格数量由133 800增至206 016时，最大压力变化率为0.386%。可认为当网格数量达到133 800时，计算结果之间的偏差在可接受范围内，与结果存在无关性。

2.4 数值模拟结果

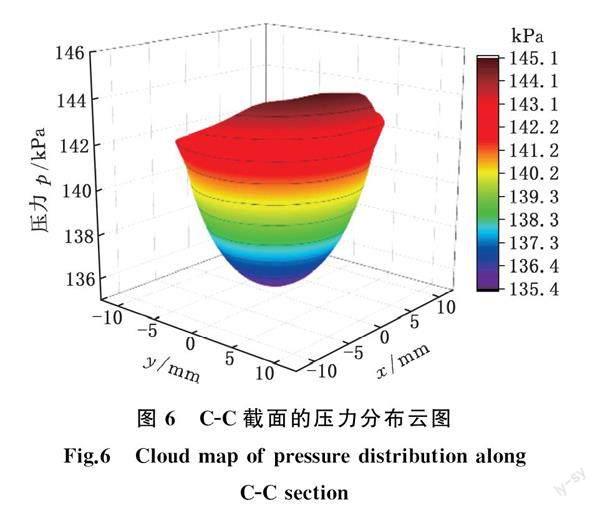
图5为圆孔直径D0=20 mm时的压力分布云图，圆孔长L=200 mm，沿磨料流动方向定义左端为入口，右端为出口，沿C-C方向剖开得到圆孔径向截面压力分布云图，为了更好地表达C-C截面的压力变化趋势，利用后处理软件对流场压力分布云图进行适当调整。由图6可知，径向上的压力衰减量很小，且同圆周上的压力也是很相近的，故需重点研究圆孔轴线方向上的压力分布。沿图5中D-D方向剖开得到轴向截面图，见图7，圆孔壁面在平面上投影为AB线，由式（4）可知材料去除量Δz与压力p成正比，因此，选取AB为数据提取线，以AB线上压力的均值和方差为标准来评判压力的大小和分布均匀性，进而反映圆孔壁面材料去除量的大小及分布均匀性。图7中AB线上0 mm处点A的压力记为p1，60 mm处点E的压力记为p2，定义局部压差Δp= p1- p2。

由于出口B处压力迅速下降至零，体现为AB线上200 mm处的压力几乎都趋于下降至零点附近，B点邻近区域压力的变化较小，因此对AB线0 ～180 mm处的压力变化进行讨论。图8所示为vin=15 m/s、D0=20 mm时初始表面粗糙度对AB线上压力的影响，可知压力随着初始表面粗糙度的增大而增大，因为粗糙度越大，壁面的粗糙度轮廓波动越大，磨粒就更易进入相邻凸起的缝隙间而产生犁削效果［18］。压力数值及其波动也十分明显，但在140～180 mm处压力随初始表面粗糙度的增大而发生的变化并不显著，这是因为磨粒在入口处与壁面发生激烈的碰撞，使得部分磨粒反弹回流，伴随着流场的发展磨粒与壁面的接触力逐渐减弱，压力值也就越来越接近。图9所示为D0=20 mm、Ra=0.296 μm时入口流速对AB线上压力分布的影响，可知压力随入口流速的增大而增大，因为入口流速越大，磨粒的动能越大，压力也就越大。上述总体变化趋势表明：初始表面粗糙度明显增大时，AB线上压力的增长并不显著。以vin=15 m/s、Ra=0.296 μm为例，进一步分析圆孔直径对AB线上压力的影响，由图10可知圆孔直径越小，压力越大，且当直径由15 mm减小至10 mm时，压力有较为明显的增大，最大增幅达61.50%。

对上述结果进行均值和方差分析，结果见表3～表5，由此可知：初始表面粗糙度越小，会在AB线上产生相对均匀且更小的压力，但影响不显著；更小的入口流速可以在AB线上产生更加均匀的压力，但产生的压力更小；更大的圆孔直径可以在AB线上产生更加均匀且更小的压力，圆孔直径对压力均匀性影响最显著，均匀性提高约52.91%，说明圆孔直径减小至一定程度时，壁面效应会越发显著。依据上述结果，可以通过减小入口流速来提高磨粒流流场压力分布的均匀性。

由图8～图10可知，随着磨料的流动，AB线上同一位置处的压力越来越接近，因此分析初始表面粗糙度、入口流速和圆孔直径对局部压差Δp的影响。图11所示为三个参数水平对AB线上局部压差的影响，其中横坐标F1、F2、F3、F4分别表示初始表面粗糙度0.296 μm、1.820 μm、3.181 μm、4.273 μm，G1、G2、G3分别表示入口流速15 m/s、20 m/s、25 m/s，H1、H2、H3分别表示圆孔直径10 mm、15 mm、20 mm。可知局部压差随着初始表面粗糙度和入口流速的减小而减小，而圆孔直径越小，局部压差却越大，由式（11）可知当D0减小时，λ在增大，壁面粗糙区对磨粒流动形态的影响更加显著，加剧了湍流程度，进而增大了能量损耗，但初始表面粗糙度对局部压差的影响也不显著。

入口处的非稳定流动会产生入口倒圆、过量切削等过抛现象［19］，影响入口处的加工效果。图12和图13以D0=20 mm、vin=15 m/s、Ra=0.296 μm为例，通过分析圆孔入口处速度与剪切力的分布來研究过抛的形成过程。由图12可知，当磨粒由大口径的夹具段流入小口径的圆孔段时，磨粒受到边界的扰动及空间减小的影响，使得磨粒在入口处无序地滑擦加工表面，致使速度骤增再逐渐趋于平稳，这就致使磨粒刚进入圆孔时剪切力最大，然后呈现降低并逐渐趋于平缓的变化趋势，进而导致磨粒在入口处对孔壁面产生过量切削，最终产生过抛现象。

由式（8）可知材料去除量Δz与剪切力τ正相关，进一步分析各参数对剪切力的影响。图14所示为D0=20 mm、vin=15 m/s时初始表面粗糙度对AB线上剪切力的影响，由图可知，剪切力随着初始表面粗糙度的减小而增大，表明初始表面粗糙度越大入口处过抛现象越弱。图15所示为D0=20 mm、Ra=0.296 μm时入口流速对AB线上剪切力的影响，由图可知，剪切力随着入口流速的增大而增大，表明入口流速越小入口处过抛现象越弱。图16所示为vin=15 m/s、Ra=0.296 μm时圆孔直径对AB线上剪切力的影响，由图可知，圆孔直径越小，在入口处的剪切力越小，但趋于稳定后反而越大，表明圆孔直径越小入口处过抛现象越弱。

3 磨粒流加工试验分析

采用Easy Flow 200挤压珩磨机进行磨粒流加工试验，该设备主要包含液压系统、夹紧系统、控制及监测系统，通过夹紧图3b所示的夹具端面以夹紧整个工件，控制及检测系统控制料缸的运动并监测加工过程。该设备可以通过设置加工时间、加工周期、入口压力等方式对工件进行加工。由材料去除函数可知，材料去除量与压力直接相关，而初始表面粗糙度状态会影响流场压力的分布，因此针对工件上的圆孔进行初始表面粗糙度的单一因素试验，控制圆孔直径、磨料浓度、加工周期、入口压力不变。

待加工工件为某航天零件42CrMo合金钢材料，工件上圆孔壁面的初始表面粗糙度、磨料相关参数与前文数值模拟中的参数设置一致，圆孔直径D0均为20 mm，长度均为200 mm。先将磨料倒入下料缸中，再将安装好的夹具与工件放置在机床的夹紧平台上夹紧，设置入口压力为2.0 MPa，加工周期设为40次往复循环，采用双向加工方式。

由数值模拟分析可知：一方面，随着初始表面粗糙度的增大，磨粒与壁面的碰撞变得激烈，加剧了流场的湍流程度，进而造成更大的能量耗散，加快了压力下降的速度，导致压力分布均匀性变差，最终使得加工后圆孔壁面的粗糙度值分布均匀性更差；另一方面，随着初始表面粗糙度的增大，壁面的粗糙度轮廓波动大，磨粒就极易进入壁面凸起的缝隙之间而产生更大的压力，增大了磨粒切入工件的深度，进而产生更大的去除量，最终使其在同一个加工周期内获得更高的材料去除率。因此，通过实验研究不同初始表面粗糙度对圆孔壁面粗糙度值的变化率和粗糙度值分布均匀性的影响规律，以验证不同初始表面粗糙度对AB线上压力大小和分布均匀性的影响规律。为便于观测，在圆孔壁面上均布a～e五个粗糙度值测量点，a点与圆孔边缘相距5 mm，见图17。五个测量点一个加工周期后的粗糙度值结果见表6，可知圆孔壁面的粗糙度值分布均匀性由好到差的排序为：抛光，镗孔，铰孔，线切割。图18所示为e点的粗糙度值变化，且对e点的粗糙度值进行重复测试，添加误差棒以表明测试结果的准确性，可知圆孔壁面的粗糙度值变化率由快到慢的排序为：线切割，铰孔，镗孔，抛光，最快约53.95 nm/次。由此可见，上述结果与表3的仿真结果相吻合。上述实验结果也很好地验证了不同初始表面粗糙度对壁面效应作用规律的影响。

选取某段流道，采用ZQ-601高清数码电子显微镜对磨粒流加工前后的四种不同工艺孔壁面进行检测，见图19。可知通过抛光获得的圆孔在经磨粒流加工后，其壁面最平滑光整，微观不平整度相较于其他三者更低，最终获得了更加均匀的表面。因此，除初始表面粗糙度值外，表面微观形貌对磨粒流光整加工过程中粗糙度值的改善也具有重要影响。

4 结论

（1）当入口流速和初始表面粗糙度越小、圆孔直径越大时，AB线上局部压差越小，其压力分布的均匀性也越好，磨粒流加工中的壁面效应越弱。

同时，各参数对AB线上压力的影响程度又是不一致的，从大到小排序如下：圆孔直径，入口流速，初始表面粗糙度，其中，圆孔直径从10 mm增至15 mm时，压力均匀性有较为明显的提高，总共提高约52.91%。在实际磨粒流加工前，可以通过减小工件在上一道工序中加工后的表面粗糙度，或者减小入口流速来提高磨粒流流场压力分布的均匀性。

（2）入口处圆孔壁面速度的突变导致剪切力突变，从而产生过抛现象。入口流速对AB线上剪切力的影响程度最大。更小的圆孔直径和入口流速、更大的初始表面粗糙度，可以在AB线入口处产生更小的剪切力，更有利于减弱入口处的过抛现象，导致壁面效应也更弱。在实际加工中可考虑在工件两端各加一段材料特性、表面形貌等与所加工圆孔一致的专用夹具，将入口处的过量切削区域转移至此夹具上，从而避免入口处产生过抛现象。

（3）对不同初始表面粗糙度的圆孔壁面进行磨粒流光整加工试验，结果表明：随着圆孔壁面初始表面粗糙度的减小，其壁面的粗糙度值分布均匀性更好，更有利于减弱磨粒流加工中的壁面效应，其分布均匀性由好到差的排序为：抛光，镗孔，铰孔，线切割；随着圆孔壁面初始表面粗糙度的增大，壁面的粗糙度值变化率更快，最快约53.95 nm/次，其变化率由快到慢的排序为：线切割，铰孔，镗孔，抛光。试验结果与表面粗糙度状态对壁面效应影响的数值模拟结果相吻合。

参考文献：

［1］CHEUNG C F， WANG C J， CAO Z C， et al. Development of a Multi-jet Polishing Process for Inner Surface Finishing［J］. Precision Engineering， 2018， 52：112-121.

［2］焦悦， 贺斌， 李朋， 等. 大深径比微孔加工技术及其发展［J］. 航空科学技术， 2018， 29（3）：1-7.

JIAO Yue， HE Bin， LI Peng， et al. Large Depth Diameter Microporous Processing Technology and Its Development［J］. Aviation Science and Technology， 2018， 29（3）：1-7.

［3］ANTUNES R A， SALADOR C A F， OLIVEIRA M C L. Materials Selection of Optimized Titanium Alloys for Aircraft Applications［J］. Materials Research， 2018， 21（2）：e20170979.

［4］刘薇娜，蔡智杰，李云峰，等.喷油嘴微孔磨粒流抛光数值模拟与试验［J］.中国机械工程，2017， 28（1）：13-19.

LIU Weina， CAI Zhijie， LI Yunfeng， et al. Numerical Simulation and Experiment of Microporous Abrasive Flow Polishing of Fuel Injector［J］. China Mechanical Engineering， 2017， 28（1）：13-19.

［5］BARAIYA R， BABBAR A， JAIN V， et al. In-situ Simultaneous Surface Finishing Using Abrasive Flow Machining via Novel Fixture［J］. Journal of Manufacturing Processes， 2020， 50：266-278.

［6］李俊烨， 朱志宝， 张心明， 等.异形截面孔磨粒流精密加工质量分析［J］.中国机械工程，2021， 32（17）：2063-2073.

LI Junye， ZHU Zhibao， ZHANG Xinming， et al. Quality Analysis of Abrasive Flow Precision Machining of Special-shaped Section Holes［J］. China Mechanical Engineering， 2021， 32（17）：2063-2073.

［7］李琛， 計时鸣， 谭大鹏， 等.软性磨粒流加工特性及近壁区域微切削机理［J］.机械工程学报，2014， 50（9）：161-168.

LI Chen， JI Shiming， TAN Dapeng， et al. Microcarpiece Processing Characteristics and Near Wall Region of Soft Abrasives［J］. Journal of Mechanical Engineering， 2014， 50（9）：161-168.

［8］SINGH H， SANKAR M R， JAIN V K. Simulation and Experimental Investigations into Abrasive Flow Nanofinishing of Surgical Stainless Steel Tubes［J］. Machining Science and Technology， 2018， 22（3）：454-475.

［9］AZAMI A， AZIZI A， KHOSHANJAM A， et al. A New Approach for Nanofinishing of Complicated-surfaces Using Rotational Abrasive Finishing Process［J］. Materials and Manufacturing Processes， 2020， 35（8）：940-950.

［10］SHARMA A K， VENKATESH G， RAJESHA S， et al. Experimental Investigations into Ultrasonic-assisted Abrasive Flow Machining（UAAFM） Process［J］. The International Journal of Advanced Manufacturing Technology， 2015， 80（1/4）：477-493.

［11］WANG A C， CHENG K C， CHEN K Y， et al. A Study on the Abrasive Gels and the Application of Abrasive Flow Machining in Complex-hole Polishing［J］. Procedia CIRP， 2018， 68：523-528.

［12］高航， 付有志， 王宣平， 等.螺旋面磨料流光整加工仿真与试验［J］.浙江大学学报（工学版）， 2016， 50（05）：920-926.

GAO Hang， FU Youzhi， WANG Xuanping， et al. Simplified Assembly and Test Simulation and Test［J］. Journal of Zhejiang University（Engineering Edition）， 2016， 50（5）：920-926.

［13］李研彪， 陈强， 张利.钛合金薄壁曲面液态金属-磨粒流加工仿真与试验研究［J］.机械工程学报，2021， 57（23）：220-231.

LI Yanbiao， CHEN Qiang， ZHANG Li. Simulation and Experimental Research on Liquid Metal-abrasive Flow Machining of Titanium Alloy Thin-walled Surfaces［J］. Journal of Mechanical Engineering， 2021， 57（23）：220-231.

［14］尹洪超， 刘宵， 翟镇德， 等. 多角度弯曲管磨粒流加工数值模拟研究［J］. 中国机械工程， 2021， 32（11）：1299-1306.

YIN Hongchao， LIU Xiao， ZHAI Zhende， et al. Numerical Simulation of Multi-angle Bending Tube Grain Flow［J］. China Mechanical Engineering， 2021，32（11）：1299-1306.

［15］张克华， 许永超， 丁金福， 等.异形内孔曲面的磨料流均匀加工方法研究［J］. 中国机械工程， 2013， 24（17）：2377-2382.

ZHANG Kehua， XU Yongchao， DING Jinfu， et al. Research on Abrasive Flow Uniform Machining Method of Special-shaped Inner Hole Surface［J］.China Mechanical Engineering， 2013， 24（17）：2377-2382.

［16］兰文涛， 吴爱祥.非牛顿流体管道流动方程及其近似解［J］. 哈尔滨工业大学学报， 2020， 52（12）：140-146.

LAN Wentao， WU Aixiang. Non-Newtonian Fluid Pipeline Flow Equation and Its Approximate Solution［J］. Journal of Harbin Institute of Technology， 2020， 52（12）：140-146.

［17］计时鸣， 李琛， 谭大鹏， 等. 软性磨粒流加工方法及近壁区域特性［J］.浙江大学学报（工学版）， 2012， 46（10）：1764-1772.

JI Shiming， LI Chen， TAN Dapeng， et al. SoftAbrasive Flow Machining Method and Properties of Near-wall Region［J］. Journal of Zhejiang University（Engineering Science Edition）， 2012， 46（10）：1764-1772.

［18］劉宵， 尹洪超， 穆林. 基于欧拉-欧拉方法的细长管道内磨粒流加工数值模拟研究［J］. 大连理工大学学报， 2021， 61（2）：143-150.

LIU Xiao， YIN Hongchao， MU Lin. Numerical Simulation of Waste Flow Processing in Employed Pipeline Based on Euler-Euler Method［J］. Journal of Dalian University of Science and Technology， 2021， 61（2）：143-150.

［19］FU Youzhi， GAO Hang， YAN Qiusheng， et al. A New Predictive Method of the Finished Surface Profile in Abrasive Flow Machining Process［J］. Precision Engineering， 2019， 60：497-505.

（编辑 陈 勇）

作者简介：

汤炉滨，男，1998年生，硕士研究生。研究方向为超精密加工。

孔凡志（通信作者），男，1976年生，副教授。研究方向为超精密加工。E-mail：franzkong@zjut.edu.cn。

收稿日期：2022-06-06

基金项目：浙江省科技计划（2021C01G6232927）；浙江省公益技术应用研究项目（LGG22E050033）