运动链基本环路集新的定义及其生成方法

孙亮波　洪熙熙　刘小翠　刘新

摘要：环路是运动链结构的固有特征，已有研究和应用多集中在基于环路的构型综合、同构判定、刚性子链消除等方面。给出了基本环路集的新定义，提出了运动链的树状结构表达及相关理论，以及基于此的基本环路集提取原则，方便快捷地获得各种运动链的基本环路集。案例分析证明，所提方法规则简单，便于计算机程序化实现，可快速地获得结构复杂、对称性高的运动链的基本环路集。通过实例证明了上述理论的正确性和有效性。

关键词：基本环路集；树状结构；最短环路；环路特性

中图分类号：TH112

DOI：10.3969/j.issn.1004-132X.2023.09.006

New Definition of Basic Loop Set of Kinematic Chain and Its Generation Method

SUN Liangbo HONG Xixi LIU Xiaocui LIU Xin

Abstract： Loops were an inherent feature of kinematic chain structures， and most of the existing researches and applications were focused on configuration synthesis， isomorphism determination and rigid sub-chain elimination based on loops. A new definition of basic loop set was proposed， and the dendrogram expression of kinematic chain and related theories were proposed， as well as the basic loop set extraction principles based on the holographic matrix expression of inter-component connection relations and complex hinge determination. The proposed method is simple in rules， easy to implement by computer programmatically， and may obtain the basic loop sets of kinematic chains with complex structures quickly， and the correctness and validity of the above theory were proved by examples.

Key words： basic loop set; dendrogram; shortest loop; loop characteristics

0 引言

运动链型综合是机械产品和机构创新设计的基础，1964年，FREUDENSTEIN等［1］首次将图论引入机构学，用于表示运动链的拓扑结构。借助图论［2］这一工具，学者们综合了大量的各种构件数和运动副数的运动链［3-4］。描述运动链的结构参数不仅有杆件数和运动副数等基本信息，还包括杆件类型、多元构件数量和类型、独立环路集、最长环路、运动副类型等信息，不同的结构参数组成大量不同的机构，这极大地丰富了机构的结构类型。Symbol`@@其中，运动链中独立环路数、最长环路及其包含的构件个数、最长环路中多元构件的排列、各个环路间的耦合关系等体现了运动链的结构特征。学者们提出基本环路集的定义［5］，采用基本环和辅助结构法用于运动链生成［6］，后续基于环路提出同构判定方法［7-8］，采用基本环路集解决刚性子链判定问题和拓扑图的自动绘制问题［5，8］。RAO等［9］对运动链的环路进行分析，得到了一些概念和定义，以及环路与铰链、构件间的不变关系式。杨廷力等［10］也提出了相关的环路特性理论。总体来说，如同构判定［11-12］、刚性子链判定［13］、最长环路［5］、拓扑图自动生成［7，14-16］等都采用环路或基本环路集进行，因此对于基本环路集，应有更严谨和可操作性的定义和生成方法，这将有助于对大量的运动链构型综合进行相应的处理。

对于结构具有一定对称性的运动链，其基本环路集的选取有多种可能。目前，关于基本环路集的自动生成，研究成果较少。DING等［7］给出了基本环路集的数学定义，通过环路的“+，-，×”操作获得运动链的其他环路和最长环路，但是对环路的获取方法并没有详细说明。LIU等［17］提出广度优先生成树求得图的基本回路，该方法生成的基本环路集只是众多环路集组合中的一种，并且不包含复铰。

对于结构复杂的多构件运动链，基于目测的网孔状环路的选取是非常困难的。同时，选择网孔状的环路作为基本环路集的环路，不适用于计算机自动化程序设计。本文给出了基本环路集的新定义，并与文献［5］进行了对比分析，提出树状结构、含复铰的运动链基本环路集提取方法，对3个实例进行分析，以此来论证所提方法的正确性和可行性。

1 基本环路集的新定义

在研究基本环路集之前，给出2个与环路有关的特性。

（1）环路特性。独立的环路是运动链中某些构件首尾依次相连构成的封闭链，因此，独立环路中不允许出现重复的运动副或构件。对于通过简单铰链连接的构件，运动副的重复必然伴随构件的重复；而对于复铰连接的构件，复铰处对应不同构件间的连接運动副，因此将复铰点置于环路中，以甄别和满足环路特性。

（2）运动链结构特性。对于闭式的可分离或不可分离运动链，任意一组基本环路集都可以唯一确定运动链的环路结构。

文献［5］给出了基本环路集的定义1：①环路集的环路数刚好等于其独立环路数；②运动链的所有其他环路都能通过基本环路集里面的环路经过“+”运算得到。

本文给出基本环路集新的定义2：①环路集的环路数等于独立环路数；②每个环路为包含其中的某个或多个构件的所有环路中的最短环路；③环路集应包含运动链中的所有构件。

上述两种定义如果不加以严格甄别是难以区别的。定义1给出了一个广泛的定义，并且其获取方式是模糊的；定义2则给出了更严格的定义，规定了基本环路集中的每个环路必须是环路中一个或多个构件的最短环路，并且给出了基本环路集的可行的获取方式。

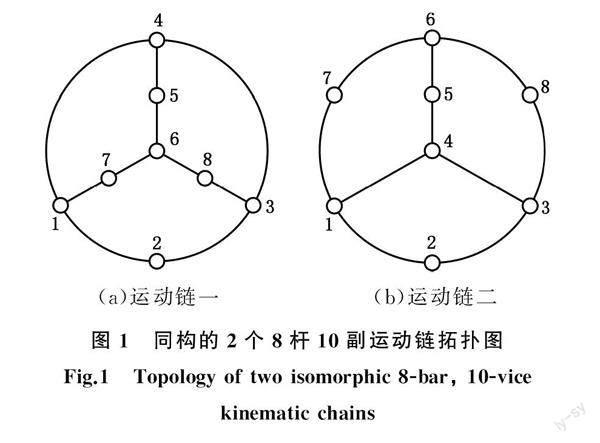
下例很好地解释了2种定义的区别。图1所示两个同构的8杆10副1自由度运动链拓扑图，根据欧拉定理的独立环路数计算公式为

L=p-n+1=10-8+1=3

其中，p为运动副个数，n为杆件数。其基本环路集包含3个独立环路。

该拓扑图为网状和非交叉，往往可以直接观测得到一组基本环路集。如果直接从网状环路判断，图1a得到的基本环路集如下。L1：1-2-3-8-6-7，L2：1-4-5-6-7，L3：3-4-5-6-8， 该环路集分别是2个5构件的环路和1个6构件的环路。由图1b得到的基本环路集如下（分别对应包含括号中构件的最短环路）。L1：1-2-3-4（构件1，2，3，4），L2：1-4-5-6-7（构件5，6，7），L3：3-4-5-6-8（构件5，6，8），上述3个环路分别是1个4构件环路和2个5构件环路。图1a中的环路1-2-3-8-6-7可以通过对图1b中的三个最短环路进行“+”运算得到。

对于结构具有一定对称性的运动链，某个构件i对应的最短环路个数Li是一个确定的数。根据欧拉定理，独立环路数L是一个较小的数值，这就意味着根据本文给出的基本环路集定义2，基本环路集的选取是從所有构件的最短环路中随机选取L个环路的操作。

2 基于树状结构的基本环路集相关理论和生成方法

在数据结构中，各元素间的从属关系用树状结构表示［18］。本文用改进的树状结构来描述机构运动链中各构件的连接关系，通过检索描述运动链获得各构件间的连接关系。当以任一构件作为树状结构的根节点时，均可获得该根节点的连接关系和环路信息。制定一定的规则，可获得以运动链中所有构件作为根结点的最短环路。

2.1 树状结构及其环路相关理论

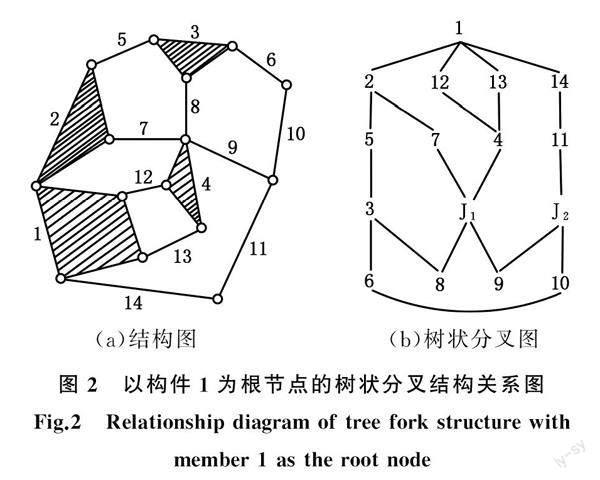
对应图2a所示运动链，图2b为以构件1作为根节点所对应的树状分叉结构关系图，用线条表示构件间的连接关系。可以看出，树状结构图能很好地表达运动链中各个构件间的连接关系，但要想编制一定的规则，通过计算机自动获得所有的环路信息或基本环路集，尤其是在含有复铰的情况下，是非常困难的。若要获得包含某个构件的最短回路，即树状结构图中包含根节点的最短回路，则相对容易得多。

由于多元构件和多元复铰的存在，用树状分叉结构表达运动链，不同于图形结构和数据结构，各个节点可以与上层节点、下层节点、同层节点有连接关系。根据构件间的连接关系和树状分叉图，给出以下定义和理论。

根节点：第一层节点为根节点。根节点只有1个。

父节点、子节点和兄弟节点：两个不在同一层且有直接连接关系的节点，上一层节点为下一层节点的父节点，反之为子节点。同层节点之间有连接关系的，称为兄弟节点。运动链中由于多元构件和多元复铰的存在，故一个父节点可能有多个子节点，一个子节点也可能有多个父节点，同时一个节点可能有多个同层的兄弟节点。

主链：根节点引出的与其子节点间的连接关系或支链称为主链。如图2b所示，树状分叉图的4条主链为1-2、1-12、1-13、1-14。

支链：根节点与2层及以上子节点构成的连接称为支链。例如图2b的树状分叉图的两条支链为1-2-5-3-6、1-14-11-10-6。

最短环路：衍生自不同主链的支链，到达同一个子节点，则构成了环路，其中包含该节点的最少构件数的环路为该根节点的最短环路。

n个长度相等的最短环路（n≥2），可能是不同主链经由不同的支链构成之间构成的，也可能是相同2个主链经由不同的支链构成的，上述最短环路全部记录为该根节点的最短环路。构件2作为根节点，

例如不同主链、不同支链构成的最短环路有：2-7-4-12-1-2，2-5-3-8-7-2。

构件14作为根节点，相同主链、不同支链构成的最短环路有：14-11-9-4-13-1-14，14-11-9-4-12-1-14，14-11-9-7-2-1-14。

2.2 基于树状结构图的基本环路集提取规则

采用树状结构表达运动链间构件的连接关系，树的深度即节点的层数，对于一个构件数的耦合运动链，其树状结构的深度约为3-4，因此检索得到树状结构的计算量相对较小。

以每一个构件作为根节点，检索到有基本环路生成，即退出检索，后续进行重复环路剔除、环路分析和选择。该方法计算和分析量较少，规则和判定条件较为简单和清晰，可快速获得运动链的基本环路集。以图1所示运动链为例，构件11检索出的树状分叉图见图3。

基于图3的树状分叉结构，提取基本环路集的规则和步骤如下。

（1）首先检索运动链中的复铰以及构成复铰的构件，若有多个复铰，则对其进行编号，如J1，J2，…，并标记其连接的构件编号。

在图3的树状分叉图中，有复铰J1（4，7，8，9）和复铰J2（9，10，11）。

（2）根据构件编号，从1开始逐一将每个构件作为树状结构的根节点，检索每个根节点的最短环路。

①检索获得与根节点有连接关系的构件，作为第2层子节点，获得该根节点下的多个主链。

检索第二层子节点为9、10和14，获得3个主链：11-9，11-10，11-14。

②由i-1层子节点i≥3检索得到与其有连接关系的i层子节点，获得并记录这些子节点到根节点的连接关系（即支链），比较不同支链间i层子节点是否相同，若相同，则获得最短环路。

若i层无相同子节点，则判断这些子节点之间有无直接连接关系，否则获得最短环路。

注意：对于结构具有对称性的运动链，上述两种情况下均可能有多条等长的最短环路，所以每一种情况均应检索所有的子节点情况。

检索图3第3层子节点1、4、6、7、8，分别对应的支链为：11-9-4、11-9-7、11-9-8、11-10-6、11-14-1。各支链之间无相同的子节点，子节点4、7、8之间有连接，但是在第3层获得的支链没有相同的节点，没有形成闭合环路，因此不予考虑。检索第4层子节点2、3、12、13，分别对应的支链为：11-9-4-12、11-9-4-13、11-9-7-2、11-9-8-3、11-10-6-3、11-14-1-2、11-14-1-12、11-14-1-13。各支链间有相同的子节点，根据最短环路定义，不同的主链引出的支链可以构成最短环路，将构件按编号从小到大排列，获得对应的4个长度为6的最短环路：1-2-7-9-11-14，1-12-4-9-11-14，1-13-4-9-11-14，3-6-10-11-9-8。

③上述最短环路的最终确定必须满足环路特性和最短环路特性，否则该最短环路无效。

要满足最短环路特性，只需要对比每条支链的第2个元素（即第2层子节点）是否相同，若不相同，则满足最短环路特性，即不同主链对应的支链能构成最短环路。

要满足环路特性，将两条支链组成环路后，根据之前的检索信息，将复铰插入相应的构件之间，检索复铰在环路中有无重复出现，若没有重复出现，则满足环路特性。

根据环路特性，将复铰插入上述最短环路中，获得相应的包含复铰的环路，即L1：1-2-7-J1-9-J2-11-14，L2：1-12-4-J1-9-J2-11-14，L3：1-13-4-J1-9-J2-11-14，L4：3-6-10-J2-11-J2-9-8。判别复铰在环路中的重复性，环路L4中具有重复的复铰，因此根因点11对应有3个最短环路L1、L2、L3。

④若步骤②中i层检索不到对应最短环路，则继续检索下一层，执行步骤②和③，直至最终获得最短环路。

（3）获得每个构件作为根节点的最短环路后，将每一个环路按照连接关系和构件编号从小到大排列，并比较这些环路，去掉重复的环路，得到最短环路集合L′。

图3所示运动链中构件1-14的最短环路检索不再赘述，各最短环路及对应的构件见表1。

由表1可以看出，构件11、14对应有3个最短环路，构件3、7、8对应有2个最短环路，其他构件按对应1个最短环路。除构件7对应的最短环路1-2-7-4-12没有重复外，其他6个环路均有重复，而该运动链的独立环路数为5。因此，优先选择重复度大的环路2-5-3-8-7、3-6-10-9-8、1-12-4-13，然后从11、14对应的3个最短环路中随机选择2个，如1-2-7-9-11-14、1-12-4-9-11-14，满足运动链结构特性，即所有环路中的构件都出现在上述环路组合中。最终得到包含所有构件的基本环路集为，L1：1-12-4-13， L2：2-5-3-8-7，L3：1-2-7-9-11-14，L4：1-12-4-9-11-14，L5：3-6-10-9-8。

（4）若L′=L，则获得的所有环路构成基本环路集。若L′>L，则在最短环路集合L′中随机抽取数量等于独立环路数L的最短环路，根据本文给出的基本环路集新的定义2中的第3条，基本环路集应包含运动链所有环路中的所有构件。

若L′

图4a中到步骤（3）获得了3个最短环路：1-2-3-4-5，6-7-8-9，10-11-12-13，检索到2个最短环路1-2-3-4-5与10-11-12-13，构件1与11有连接关系，因此，1-11作为检索的第一层节点，按照上述规则，可最终检索出包含1-11的最短环路1-5-4-6-9-10-11，获得上述5个最短环路集。同理，图4b中到步骤（3）获得4个最短环路：1-2-3-4，5-6-7-8-9，10-11-12-13，14-15-16-17-18，检索到构件4和17有连接关系，以4-17作为第一层节点，可检索到3-4-17-18-9-5。继续检索，以8-10为第一层节点，可检索到8-9-18-14-13-10，最终可获得上述6个环路的最短环路集。

以上基本环路集的获取规则，对于构件数较少或结构不对称的运动链，一般不需要进行步骤（3）操作即可得到与基本环路数对应的基本环路集；而对于构件数较多且结构对称性高的运动链，可能会出现最短环路数多于基本环路数的情况，依据上述优化选择方法，可大大减少分析对比计算量，快速获得基本环路集。

3 最短环路集分析实例

3.1 可分离运动链的基本环路集

可分离运动链大量应用于机械手和机器人，对于可分离运动链的基本环路集，获得复铰信息，再根据环路特性判定最短环路。

图6所示的运动链，若不考虑复铰J1，检索构件1的最短环路会得到1-2-3-4-5的最短环路，注意到复铰J1连接构件1、2、5、10，因此，将复铰插入相应的位置后得到的环路为1-J1-2-3-4-5-J1，该环路有复铰重复出现，不应作为构件1的最短环路。

该可分离运动链的最短环路集为：1-6-7-8-9-10，2-3-4-5，分别对应环内所有构件的最短环路。

3.2 具有较大对称性的运动链的环路集

图7为28构件、具有较大对称性的运动链拓扑图［19］，根据欧拉公式计算其独立环路数L=p－n+1=13。如以三元构件1作为根节点，检索获得的最短8构件环路有19个，而以二元构件3作为根节点，检索获得的最短8构件环路有8个。根据本文的定义和操作规则，限于篇幅，仅直接给出该运动链的一组基本环路集：1-2-3-4-5-6-13-14， 1-2-9-8-7-27-25-26，1-14-13-6-5-18-19-26，1-14-13-12-11-24-25-26，1-14-15-22-21-20-19-26，2-3-4-5-18-17-10-9，2-3-4-23-22-21-8-9，4-5-6-13-14-15-22-23，4-5-18-17-10-11-24-23，4-5-18-19-20-21-22-23，7-8-9-10-11-24-25-27，10-11-24-23-22-15-16-17，11-12-28-20-19-26-25-24。

4 讨论

（1）基本环路集是运动链的重要结构特性，由一组基本环路集可以反向推导出运动链的确定结构，运动链型综合过程中的其他关键问题（如刚性子链消除、拓扑图和结构图的自动绘制等），也可在本文的研究基础上进一步深入或优化研究。

（2）本文提出的基本环路集定义严谨，获取方法简单，获取过程中只需要检索构件之间的连接关系以及环路之间的重复性对比等，易于程序化设计实现，且计算分析量较小。

5 结论

（1）本文提出了基本环路集新的严密、生成便利的定义。

（2）提出了表达运动链构件间连接关系的树状结构图和相关理论，基于树状结构图和全息矩阵，阐述了基本环路集的生成规则和步骤，进一步提出了具有较多构件或较高对称性的运动链的基本环路集的优化选择方法。

（3）分析了几个运动链的基本环路集提取方法，通过这些实例证明了本文所提方法具有规则简单、可靠性好、计算量小，可快速地获得运动链的基本环路集等优点。

参考文献：

［1］FREUDENSTEIN F， DOBRJANSKYJ L. On a Theory for the Type Synthesis of Mechanisms［M］∥Applied Mechanics. Berlin：Springer，1966：420-428.

［2］卢开澄.图论及其应用［M］.北京：清华大学出版社，1984：3-20.

LU Kaicheng. Graph Theory and Its Applications［M］. Beijing：Tsinghua University Press， 1984：3-20.

［3］杨廷力.机械系统基本理论——结构学·运动学·动力学［M］.北京：机械工业出版社，1995：1-69.

YANG Tingli. Basic Theory of Mechanical Systems—Structure， Kinematics， Dynamics［M］. Beijing：Machinery Industry Press， 1995：1-69.

［4］曹惟庆.连杆机构的分析与综合［M］.2版.北京：科学出版社， 2002：1-8.

CAO Weiqing. Analysis and Synthesis of Linkage Mechanisms［M］.2nd ed.Beijing：Science Press， 2002：1-8.

［5］丁华锋.运动链的环路理论与同构判别及图谱库的建立［D］.秦皇岛：燕山大学，2007.

DING Huafeng. Loop Theory and Isomorphic Discrimination of Kinematic Chains and the Establishment of a Library of Graphs［D］. Qinghuangdao：Yanshan University， 2007.

［6］宋黎， 廖愛红， 聂松辉. 含复铰有移动副平面机构运动分析数学模型的自动建立方法［J］. 机械科学与技术， 2015， 31（2）：213-218.

SONG Li， LIAO Aihong， NIE Songhui. An Automatic Method for Establishing Mathematical Models for Motion Analysis of Planar Mechanisms Containing Complex Hinges with Moving Subassemblies［J］. Mechanical Science and Technology， 2015， 31（2）：213-218.

［7］DING Huafeng， HUANG Zhen. A New Theory for the Topological Structure Analysis of Kinematic Chains and Its Applications［J］ Mechanism and Machine Theory， 2007， 42（10）：1264-1279.

［8］丁华锋，黄真.平面机构统一拓扑描述模型的建立及同构判别［J］.机械工程学报，2009，45（3）：99-103.

DING Huafeng， HUANG Zhen. Establishment of a Unified Topological Description Model for Planar Mechanisms and Isomorphism Discrimination［J］. Journal of Mechanical Engineering，2009，45（3）：99-103.

［9］RAO A C， DESHMUKH P B. Computer Aided Structural Synthesis of Planar Kinematic Chains Obviating the Test for Isomorphism［J］. Mechanism and Machine Theory， 2001，36（4）：489-506.

［10］杨廷力，罗玉峰，张策，等.回路秩、通路约束度与图耦合度及其应用［J］.自然科学进展，2004，14（10）：1156-1163.

YANG Tingli， LUO Yufeng， ZHANG Ce，et al. Loop Rank， Pathway Constraint Degree and Graph Coupling Degree and Their Applications［J］. Advances in Natural Sciences， 2004，14（10）：1156-1163.

［11］黄真， 丁华锋. 多环运动链环路代数基础理论的建立及其应用［J］. 中国科学：E 辑， 2007， 37（7）：904-913.

HUANG Zhen， DING Huafeng. Establishment of Algebraic Ground Theory of Multi-loop Kinematic Chain Loops and Its Applications［J］. Chinese Science：Series E， 2007， 37（7）：904-913.

［12］李树军， 宋桂秋， 杜立群， 等. 用拓扑特性矩阵辨识运动链的同构体及机架变换研究［J］. 机械工程学报， 2002， 38（1）：149-153.

LI Shujun， SONG Guiqiu， DU Liqun， et al. Identification of Isomorphs of Kinematic Chains by Topological Characteristic Matrix and Study of Frame Transformation［J］. Journal of Mechanical Engineering， 2002， 38（1）：149-153.

［13］张瑶. 平面八杆含复铰杆组型综合研究［D］. 武汉：武汉科技大学， 2019.

ZHANG Yao. A Comprehensive Study on the Group Type of Planar Eight-bar Containing Compound Hinge Bar ［D］. Wuhan ：Wuhan University of Science and Technology， 2019.

［14］赵瑞清， 陈克西. 带框矩阵及其在图论中的应用［J］. 桂林电子工业学院学报， 1985（1）：37-48.

ZHAO Ruiqing， CHEN Kexi. Framed Matrices and Their Applications in Graph Theory［J］. Journal of Guilin Institute of Electronics Technology， 1985（1）：37-48..

［15］袁勇. 基于閉环运动链图谱库的可分离结构运动链的自动综合［D］. 秦皇岛：燕山大学，2012.

YUAN Yong. Automatic Synthesis of Kinematic Chains of Separable Structures Based on Closed-loop Kinematic Chain Mapping Library［D］. Qinghuangdao：Yanshan University，2012.

［16］张锦丽. 基于图谱库的平面4和6自由度可分离运动链自动结构综合［D］. 秦皇岛：燕山大学，2014.

ZHANG Jinli. Automatic Structural Synthesis of Planar 4- and 6-degree-of-freedom Separable Kinematic Chains Based on Atlas Library［D］. Qinghuangdao：Yanshan University，2014.

［17］LIU Yong， XIAO Renben. New Approach to Automatic Sketching of Planar Kinematic Chains Based on Loop Configuration and Its Computerization［J］. Chinese Journal of Mechanical Engineering，2002，38（6）：21-27.

［18］陈世敏.树状结构大数据类型的高效支持［J］.大数据，2018，4（4）：35-43.

CHEN Shimin. Efficient Support for Tree-structured Big Data Types［J］. Big Data，2018，4（4）：35-43.

［19］DING H， HUANG Z. Isomorphism Identification of Graphs：Especially for the Graphs of Kinematic Chains［J］. Mechanism and Machine Theory， 2009， 44（1）：122-139.

（编辑 陈 勇）

作者简介：

孙亮波，男，1979 年生，教授、博士。研究方向为机械设计及理论。E-mail：sunlb1979@163.com。

收稿日期：2022-06-01

基金项目：国家自然科学基金（51875418）