例析抽象函数问题的特殊化思想求解策略

福建省漳州实验中学 (363000) 方细贤

在导数及其应用的客观题中,有一类不给出具体的函数解析式,只给出函数f(x)满足的一些条件,需根据这些条件,探究f(x)所具有的性质的题目.此类问题能够全面考查同学们对函数的概念和性质的理解,但因为“抽象”,很多同学对这类问题感到茫然,找不到解题突破口.

基于特殊化思想,我们可以尝试,通过构造具体函数满足题设要求,再从具体函数出发对问题进行求解,以规避繁杂的转化过程,优化整个解题过程.笔者通过总结,归纳出应用特殊化思想求解抽象函数问题的策略:罗列出抽象函数满足的所有条件;根据条件的结构特点,尝试以简单初等函数(指数、对数、幂函数、三角函数等)为基本素材,经过适当的组合(加、减、乘、除、复合)构造出具体函数,从而对问题进行分析求解.

本文通过几个典型例子,阐述上述策略在求解抽象函数问题中的应用.

1、将抽象函数特殊化为常数函数

A.(-∞,2)B.(1,+∞)

C.(-∞,1)D.(2,+∞)

2、将抽象函数特殊化为一次函数

A.(0,2) B.(2,+∞)

3、将抽象函数特殊化为二次函数

例3 (2021届重庆市高三数学第一次诊断第8题,单选)已知定义在R上的可导函数f(x)的导函数为f′(x),f(x)=f(-x),当x>0时,f′(x)>2x,则关于x的不等式f(2-x)-f(x)>4-4x的解集为( ).

A.(-∞,-1)∪(1,+∞) B.(-1,+∞)

C.(-∞,1) D.(-1,1)

分析：本题若正面求解,需要通过f′(x)>2x构造函数F(x)=f(x)-x2,将不等式f(2-x)-f(x)>4-4x变形为F(2-x)>F(x),利用F(x)的单调性和奇偶性得到|2-x|>|x|,得到x<1.整个过程思维量较大,基于特殊化思想,结合题设条件,我们可以尝试令f(x)为某个常见的函数.

解析：函数f(x)满足条件:①f(x)=f(-x);②当x>0时,f′(x)>2x.由条件f(x)=f(-x),得f(x)为偶函数,尝试令f(x)=ax2+c.当x>0时,f′(x)>2x,得2ax>2x,只需a>1即可,特别地,取f(x)=2x2.当f(x)=2x2,不等式f(2-x)-f(x)>4-4x即2(2-x)2-2x2>4-4x,化简得4x<4,解得x<1,排除其他三个选项,故选C.

4、将抽象函数特殊化为三角函数

例4 (2021年全国新高考Ⅱ卷第8题,多选)设函数f(x)的定义域为R,且f(x+2)为偶函数,f(2x+1)为奇函数,则( ).

C.f(2)=0 D.f(4)=0

分析：正面求解本题需要分别通过f(x+2)为偶函数,f(2x+1)为奇函数,得到相关的两个等式,再将两个等式通过代换,进行关联,再得到第三个等式,在此基础上得到f(x)的对应性质,实现问题的求解.这样的求解过程,思维量加大,大部分学生难以完成.由f(x+2)为偶函数,得f(x)图象关于x=2对称,由f(2x+1)为奇函数,得f(x)图象关于(1,0)对称,考量同时具有轴对称和中心对称的函数,自然能够联想到将f(x)特殊化为某个三角函数.

C.f(-1)=f(4) D.g(-1)=g(2)

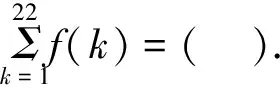
A.-3 B.-2 C.0 D.1

分析：本题的常规解法是通过计算特殊值,再通过解析式的变换,求解得到函数f(x)周期,再借助周期及前6个函数值,求得最终的结果,整个过程思维量较大,需要学生有较强的恒等变换能力.关注到本题题设条件具有一般性,但是结果具有恒定性,关注题设条件中f(x+y)+f(x-y)=f(x)f(y)的模型特点,与2cosxcosy=cos(x+y)+cos(x-y)这一关系式结构相似,通过类比,可尝试将f(x)的表达特殊化为某个余弦函数.

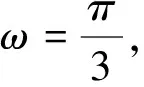
基于特殊化思想,通过构造具体函数,实现了一类抽象函数问题的轻松求解,彰显了数学思想在解题过程中的引领作用.在日常解题过程中,老师们应引导学生尝试换一个角度去思考问题,可能会对问题有更深刻的认识,获得不一样的学习体验.