基于目标规划的语言值OWA算子及其在大学生综合测评的应用

林君雅,陈豪,杨昔阳*

(1.泉州师范学院 数学与计算机科学学院,福建 泉州 362000;2.福建省大数据管理新技术与知识工程重点实验室,福建 泉州 362000;3.智能计算与信息处理福建省高等学校重点实验室,福建 泉州 362000;4.数字福建智能制造大数据研究所,福建 泉州 362000)

大学生综合素质评价不仅关系着高校的办学导向,也为学生的个性化发展起到引导性的作用.综观目前较为常见的综合测评方法,大多采用构建综合测评量化指标体系,对评价对象在各指标的得分进行加权综合.其难点在于指标权重的分配.例如,基于层次分析法的第二课堂综合测评[1],基于熵值法的大学生创新能力评价[2]和基于模糊综合评判的模糊综合评判[3].这类评价方法的缺点在于无法鼓励学生发挥自己的特长,评价者无法根据学生的特长使用不同的指标权重.例如将学科竞赛和学业成绩两个指标的权重都设置为0.5,甲在两个指标的得分均为80分,乙在两个指标的得分分别为100分和60分.在鼓励学生发挥特长的场合,乙优于甲;但是按照加权综合计算,两者的得分相等.此外,在一些场合,学生的许多指标适合采用语言值进行评价,数值型的综合评测算法无法直接处理语言指标值.

有序加权平均(OWA)算子;目标规划;高斯模糊集;综合测评;语言值;大学生(ordered weighted averaging,OWA)算子[4]是解决此类学生综合测评问题的方法之一.OWA算子已广泛应用于医疗设备评价[5]、生态评价[6]、交通系统评价[7]等.从文[8-9]关于OWA综合评价方法的研究进展分析可以发现,语言值OWA算子和OWA权重的优化是两个重要的研究方向;将OWA算子应用于大学生综合测评的研究尚不多见.一些学者基于模糊集合提出语言值OWA算子.例如Xu提出不确定语言值OWA算子解决了群决策问题[10],Herrera等提出一种不平衡模糊语言值并将其应用于OWA算子中[11],Yu等在犹豫模糊集的假设下提出一种基于最小调整量的模糊语言值OWA方法[12],Serrano等提出基于一型模糊集的语言值OWA方法[13],杜文胜等提出一种模糊诱导OWA(FIOWA)算子[14].在许多场合,诸如“较好”“一般”的语言值比数值更适合描述属性值,因此语言值也广泛应用于各类综合评价[15].然而,语言值缺乏明显的序关系,因此有必要通过定义语言值的距离确定序关系,再将它应用于OWA算子.

OWA算子的另一个研究热点是权重的优化,文[16]综述了近些年权重优化研究的进展.一种常见的方法是利用先验的概率分布生成OWA的初始权重[17],例如正态分布[18],二项式分布[19]等.另一种方法是基于“orness”[1]的概念,利用规划模型确定OWA的权重.文[20]综述了基于熵最小原则构建的数学规划模型.此外,权重的方差[21]、χ2值[21]、最大不一致度[22]也常常作为数学规划模型的目标函数,极小化数学规划模型便可以获得合理的算法.

1 预备知识

1.1 OWA算子

定义1[9]OWAW算子根据评价对象的n维属性值(a1,a2,…,an)和n维权重向量W=(w1,w2,…,wn)给出评价对象的综合评价值,即

(1)

OWAWmax(a1,a2,…,an)=b1;

(2)

反之,如果评价者只关心表现最差的属性值,则可以取权重向量Wmin=(0,…,0,1),此时有

OWAWmin(a1,a2,…,an)=bn.

(3)

因此,设置合理的权重是OWA算子的一个重要研究课题.合理的权重应该反映评价者的乐观程度,将评价结果设置在最好和最差的属性值之间.

1.2 Orness值

定义2权重W=(w1,w2,…,wn)的Orness值[24]可以写成

Yager在文[4]中提出的Orness值α(W)可以看作是评估者乐观水平的度量.一方面,有

当且仅当w1=1,w2=w3=…=wn=0时,α(W)=1,此时OWAW是式(2)的最乐观评价.另一方面,有

当且仅当w1=w2=…=wn-1=0,wn=1时,α(W)=0,此时OWAW是式(3)的最悲观评价.

1.3 高斯模糊集

正如正态分布是最常见的连续型随机变量的分布,高斯模糊集也是常用的模糊集合之一,高斯模糊集G(μ,σ)的隶属度函数可以写成

(5)

它表示“大约为μ,不确定程度为σ”的语言值.当x=μ时,隶属度为1,表示x百分之百属于语言值G.

当μ=60,σ=10时,G(μ,σ)的隶属度图像如图1所示,其中x轴表示取值,y轴表示该值的隶属度.Rλ(G(μ,σ))={x|f(x;μ,σ)≥λ}称为G(μ,σ)的λ截集.

图1 高斯模糊集的隶属度函数

2 基于熵最优权重目标规划模型

基于熵和Orness值的概念,提出一种融合主客观因素的目标规划模型(goal programming model,GPM),用以生成OWA算子的权重,并且给出这类目标规划模型的性质.该目标规划模型即考虑到了评价者的主观乐观水平,也考虑到了权重的客观最大熵原则,因此可以合理地给出OWA算子的权重向量.

所设计的目标规划模型(GPMα)为

(6)

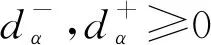
可以证明,由GPMα确定的最优权重具有以下的对称性质.

(7)

从GPM1-α的约束条件还可以发现

(8)

由式(7)可得

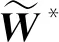
(9)

该定理表明,乐观系数为α对应的最优权重,正好是乐观系数为1-α对应的最优权重的倒序排列,说明所提出的模型具有优良的对称性。

3 高斯模糊集的运算性质

在学习成绩评价的场合,学生的学科成绩有时是以等级语言值给出的,例如“优秀”“良”中“及格”“不及格”等,而这些语言值可以通过高斯模糊集刻画.高斯模糊集通过隶属度函数描述各个(分数)数值属于某个语言值等级的程度.基于高斯模糊集的评价可以由评价者(科任教师)给出,也可以收集该课程多次考核成绩,拟合出一个语言属性值G(μ,σ).由于OWA和IOWA算子都需要对属性值进行数乘运算和求和运算,因此有必要定义模糊集的数乘和加法运算.

3.1 高斯模糊集的运算

使用高斯模糊集来描述学生的分数有两个方面的优点:一是模糊集的高斯隶属函数与广泛使用的正态分布函数非常类似,和有明确的现实意义;二是高斯模糊集的线性运算具有和实数线性运算非常类似的形式.

定理2多个高斯模糊集G(μ,σ)的线性组合仍然是一个高斯模糊集,即有

(10)

其中:系数W=(w1,w2,…,wn)∈Rn可以视为G(μi,σi),i=1,2,…,n的权重.

(11)

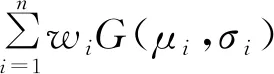
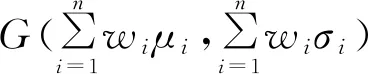
该结果表明,高斯模糊集的线性运算具有优良的运算性质:多个高斯模糊集G(μi,σi)的数乘运算的结果是对应参数μ和σ的对应数乘运算。

3.2 高斯模糊集的排序

高斯模糊集是一种常见的描述模糊语言值的工具,其原因在于高斯模糊集参数个数少,含义明确,而且它们还具有如定理1和定理2所示的优良性质.OWA算子需要对模糊语言属性值进行排序,再配合优化权重进行加权综合.为了区分各个评价对象的优劣,需要对基于高斯模糊集的模糊语言值进行排序.因此,有必要设计一种针对高斯模糊集的排序算法.

高斯模糊集包含两类参数,均值μ表示评价的平均值、标准差σ表示评价的标准差.通常,评价者希望评价均值μ越大越好,也希望评价的波动σ越小越好.基于此,一个高斯模糊集的评价可以写成

f(G(μ,σ))=ω1μ+ω2(-σ).

(12)

其中:ω1,ω2≥0,ω1+ω2=1反映了评价者对评价均值和标准差的重视程度.当ω1=1,ω2=0时,评价者只关心评价结果的均值;当ω1=0,ω2=1时,评价者只关心评价结果是否稳定.通常,合理的评价方法是这两者的折中.基于式(12)便可以对OWA算子得到的模糊语言值进行排序.

4 基于高斯模糊集和优化权重的GOWA评价方法

基于优化权重和高斯模糊集给出一种新的GOWA(Gaussian fuzzy OWA)算子,它可以用来处理评价对象的属性值为高斯模糊语言值的决策问题.

(13)

基于GOWA的多属性综合评价模型,可以概括为如下几个步骤.

步骤1优化OWA权重.给定Orness值α和权重系数β1,β2.基于采用基于式(6)的目标规划模型GMPα确定优化权重W.

步骤2确定模糊语言属性值.对于第i个评价对象,根据评价者的语言值评价或者多个历史数值成绩,构建基于高斯模糊集的语言属性值{Gij(μij,σij)|j=1,2,…,n},n是属性值的个数.在后一种情况中,μij为多个数值数据的平均值,σij为数值数据的标准差.

步骤3计算评价结果.采用式(13)计算最终评价结果Gi.

步骤4基于式(12)计算评价对象的排序.

在式(13)中,各个属性的权重完全由目标规划模型(6)确定.在多数场合下,评价者在所构建的评价体系往往对各个属性的权重赋予了初值.为了兼顾主客观因素,可以将式(13)改写为

(14)

5 基于目标规划的语言值GOWA算子的大学生综合测评

以某专业49名学生的综合测评为例,介绍基于目标规划的语言值OWA算子的应用.高校重视学生的综合测评工作,为促进学生身心健康、全面发展,创新德智体美劳过程性评价办法,建立以品行考评(F1)、学业考评(F2)、竞赛考评(F3)3个指标的综合测评体系.其中,品行考评以政治态度、品德修养、集体观念等思想政治素质为评价指标,其语言属性值由辅导员确定;学业考评以学期各门课程的学分绩点为评价标准,其高斯模糊语言属性值的参数μ,σ由所有课程学分绩点的平均值和标准差给出;竞赛考评以学科竞赛、文体活动等个人特长为评价指标,该数值型属性值由各类竞赛加分求和而得,可以看作是σ=0的高斯模糊语言值.

收集49个学生的综合测评语言指标(属性)值,如表1所示.评价者希望根据每个学生在这3个指标上的表现,给出一个语言值评价.考虑用5个语言值(优秀、良、中、及格、不及格)来评价学生,采用高斯模糊集刻画这些语言值,其隶属函数如表2和图2所示.

表1 综合测评的语言属性值

表2 评价等级

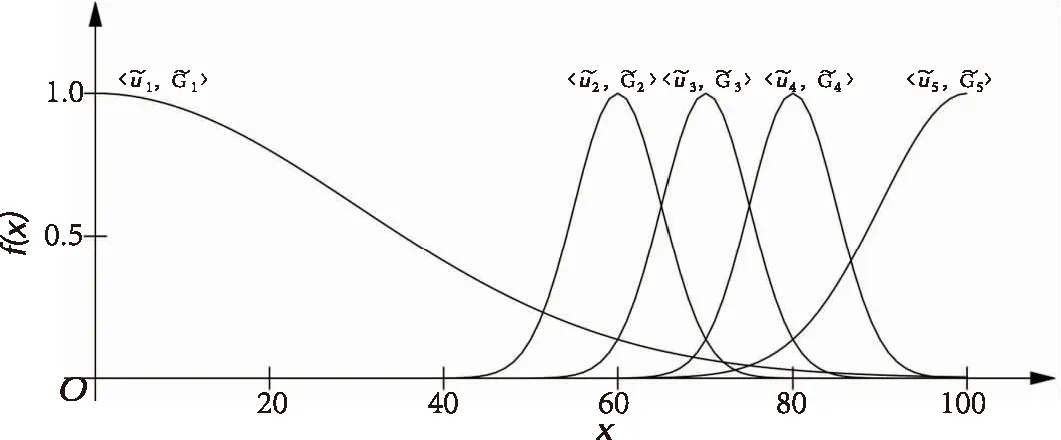
图2 基于高斯模糊集的语言值评价

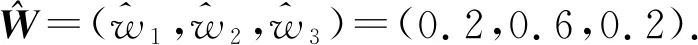
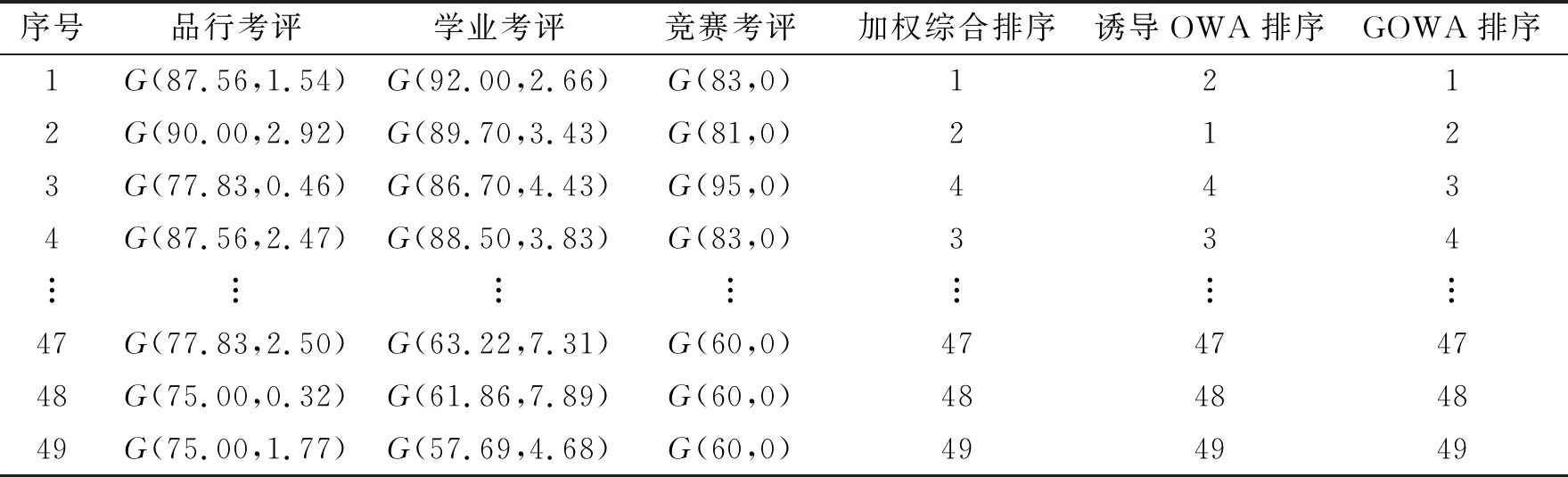
表3 班级综合评价评价结果

6 总结

传统的OWA算子可以对具有数值属性值的对象进行评价.然而在大学生综合评价的场合,许多属性值往往具有语言值描述。本文提出了一种基于高斯模糊集的GOWA综合评价方法,制定了高斯模糊集的数乘运算,并针对综合测评的场合提出了一种新的高斯模糊集的排序方法.为了鼓励大学生发展特长,设计了一种结合评价者乐观水平和熵值的目标规划模型,得到了综合主客观因素的综合评价权重,所得出的目标规划模型具有良好的对称性.大学生综合测评的实验结果表明,所提出的模型可以得到与主观感觉一致的评价结果,在某方面表现突出的学生,可以获得较好的排名,说明设置适当的乐观水平后,新的评价方法可以鼓励学生发挥自己的特长.