基于评价信息满意度的群体信息集结方法
宫诚举,郑 红,李玲玉,郭亚军
(1.哈尔滨工程大学 经济管理学院,哈尔滨 150001;2.东北大学 工商管理学院,沈阳 110169)
0 引言
综合评价是指对被评价对象所进行的客观、公正、合理的全面的评价[1]。如何集结各评价者的评价信息是群体评价需要解决的关键问题,常用的集结方法主要有线性加权综合法、非线性加权综合法、理想点法等。而目前对于群体评价中的信息集结方法以算子集结方法的研究最为广泛,文献[2,3]分别提出了加权算术平均(WAA)算子和加权几何平均(WGA)算子,这两种算子在集结过程中主要考虑评价者或评价信息自身的重要程度。文献[4,5]分别提出了有序加权平均(OWA)算子和有序加权几何平均(OWGA)算子,这两种算子则是在集结过程中考虑评价信息的位置权重,与评价信息自身的重要程度无关。文献[6,7]则是对上述四种算子的扩展,以适用于不同的评价活动。文献[8,9]则是在上述算子的基础上提出了密度加权平均(DWA)算子和密度中间(DM)算子,这两种算子在信息集结过程中考虑了属性分布的疏密程度。文献[10]提出了一种兼顾“功能性”和“均衡性”的组合集结模式,目的是在信息集结过程中综合多种集结方法的优点。
尽管关于群体评价中评价信息集结方法的研究已有丰硕的成果,但是已有的研究基本上都存在一个问题,即信息集结过程中的评价者权重是不变的。而事实上,由于各评价者的知识背景、实践经验以及看待问题的角度不同,不同评价者对同一被评价对象在同一评价指标下的认知程度不尽相同,同一评价者对不同被评价对象在不同评价指标下的认知程度也不尽相同,因此应在信息集结的过程中针对集结对象中不同元素(指表1和表2中的单个数值)赋予不同的评价者权重,使集结结果更加贴近现实。针对上述问题,本文引进评价信息满意度概念,从评价信息离散程度的角度对评价信息满意度进行界定,提出了一种基于评价信息满意度的群体信息集结方法,以解决上述分析中发现的问题。

表1 各评价者的指标赋值

表2 各评价者的评价结果
1 问题描述与假设条件
1.1 问题描述
对于一个群体评价问题,设评价者的集合为S=被评价对象的集合为评价指标的集合为存在不同看法或具有利益冲突的评价者对不同的被评价对象在不同指标下的赋值以及最终的评价值也不尽相同,设xijk表示评价者sk对于被评价对象oi关于评价指标xj的赋值,其中i=1,2,⋅⋅⋅,p,j=1,2,⋅⋅⋅,m,k=1,2,⋅⋅⋅,n,不 失 一 般性,令m,n,p≥3,由xijk组成的评价信息矩阵如表1所示。yik为评价者sk给出的被评价对象oi的评价值,由yik组成的评价信息矩阵如表2所示。目前大多数以固定的评价者权重代替评价者所有评价信息重要程度的集结方式缺乏一定的公平性,将会降低集结成的群体信息的准确度和可接受程度,因此,如何在信息集结的过程中确定各评价者不同评价信息的重要程度是群体评价研究中值得考虑的问题。
1.2 假设条件
(1)评价者熟悉评价问题所属的相关领域,具备参与评价的愿望及能力;
(2)评价问题在实际生活中获得广泛关注,评价者对该评价问题的评价信息完备;
(3)本文仅考虑评价信息由评价者主观给出的情况,且大部分评价者能够给出比较贴近实际情况的评价信息。
2 信息集结方法
2.1 评价信息满意度矩阵的确定
2.1.1 指标信息满意度矩阵的确定
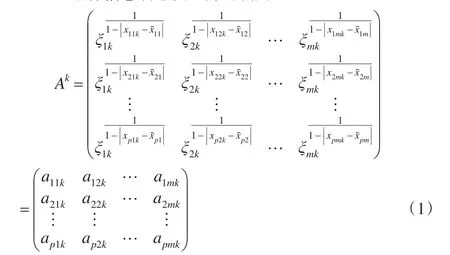
其中Ak表示构造的评价者sk的个体指标信息满意度矩阵,ξjk表示由评价者sk的指标信息矩阵得出的评价指标xj提供信息量的大小表示评价者sk对被评价对象oi在第评价指标xj下的赋值与所有评价者对其赋值的均值的距离表示评价者sk被评价对象oi在评价指标xj下的赋值与所有评价者对其赋值的平均值的偏离程度,其中1,2,…,p,j=1,2,…,m,k=1,2,…,n。
可采用的是熵值法计算ξjk[1]。在本文中,对于每一个个体指标赋值矩阵,熵值越大,表示这个指标在这个个体指标信息矩阵中的差异越小,即它所包含的信息量越少,同理,当熵值越小,表示这个指标在这个个体指标信息矩阵中的差异越小,即它所包含的信息量越大。熵值法的具体计算过程如下:
(1)计算被评价对象oi在各评价者的各评价指标下的特征比重

(2)计算各评价者的各评价指标的熵值

(3)计算各评价者的指标信息矩阵中指标xj包含的信息量ξjk

其中ξjk∈(0,1)。
ξjk表示根据各指标包含信息量的大小反映各评价者对各指标赋值的满意程度,ξjk越大说明评价者sk对指标xj赋值的满意程度越高,反之说明评价者sk对指标xj赋值的满意程度越低从各评价者对同一被评价对象在同一指标下的赋值与所有评价者对其赋值的均值的偏离程度反映各评价者对不同被评价对象在不同指标下赋值的满意程度,偏离程度越低说明满意程度越高,反之,偏离程度越高说明满意程度越低。
2.1.2 评价结果满意度矩阵的确定
评价结果满意度矩阵的确定方法与指标信息满意度矩阵的确定方法类似,不同的是评价信息满意度矩阵的个数与评价者的个数相同,而评价结果满意度矩阵只有一个。
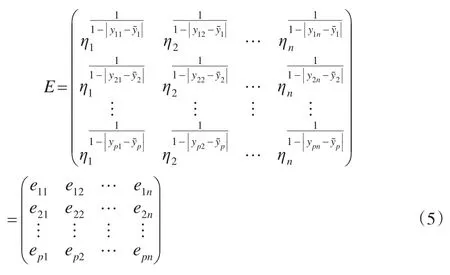
其中ηk表示评价者sk给出的所有被评价对象的评价值提供的信息量大小,计算方法与熵值法相同,表示评价者sk给出的被评价对象oi的评价值与所有评价者给出的被评价对象oi的评价值的均值的偏离程度,其中
2.2 集结过程中评价者权重的确定
由于群体评价中各评价者的知识水平、实践经验以及看待问题的角度不尽相同,因此不同评价者对同一被评价对象在同一评价指标下的认知情况不同,同一评价者对同一被评价对象在不同评价指标下的认知程度也不同,因此,群体评价的信息集结过程中应对各评价者评价信息矩阵中的不同元素赋予不同的权重。
2.2.1 集结信息为指标信息时评价者权重的确定
(1)各评价者对各被评价对象的总体认知程度αk的确定

其中bik表示评价者sk从总体上对被评价对象oi认知的稳定程度,dik表示评价者sk从总体上对被评价对象oi的认知高度,λ1,λ2为参数,且λ1+λ2=1,用于反映评价需求者的态度,当λ1>λ2时,表示更注重评价者的认知高度,当λ1<λ2时,表示更注重评价者认知的稳定程度,当λ1=λ2,表示对评价者的认知高度和认知稳定性持平等的态度。bik和dik的计算方法如下:
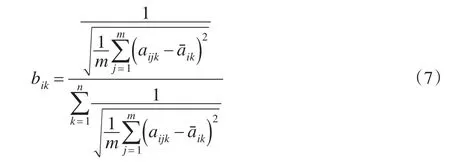
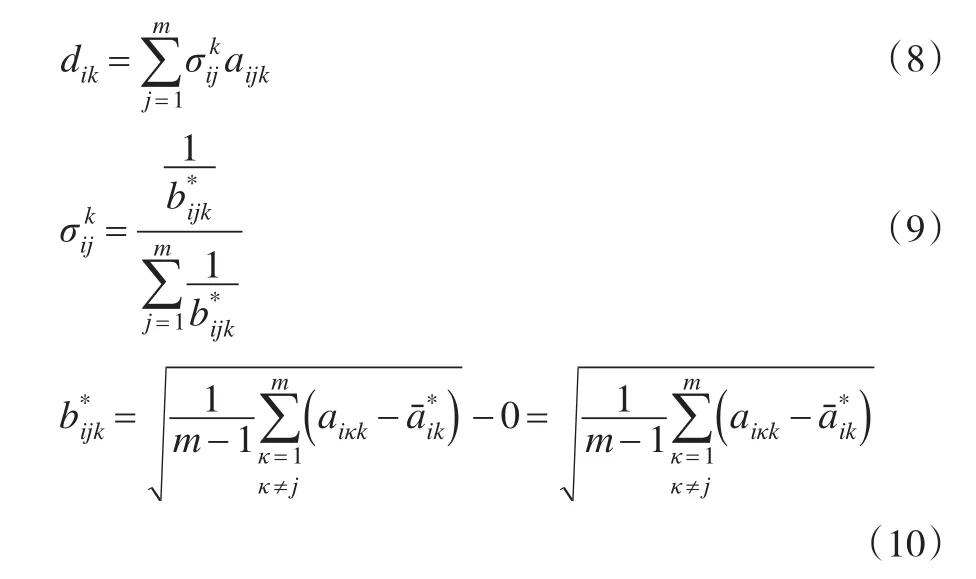
2.2.2 各评价者对各评价指标的总体认知程度βk的确定

其中gik表示评价者sk从总体上对评价指标xj认知的稳定程度,hik表示评价者sk从总体上对评价指标xj的认知高度,λ1,λ2为参数,意义同上。gik与hik的计算方法与bik和dik的计算方法类似,如下所示:

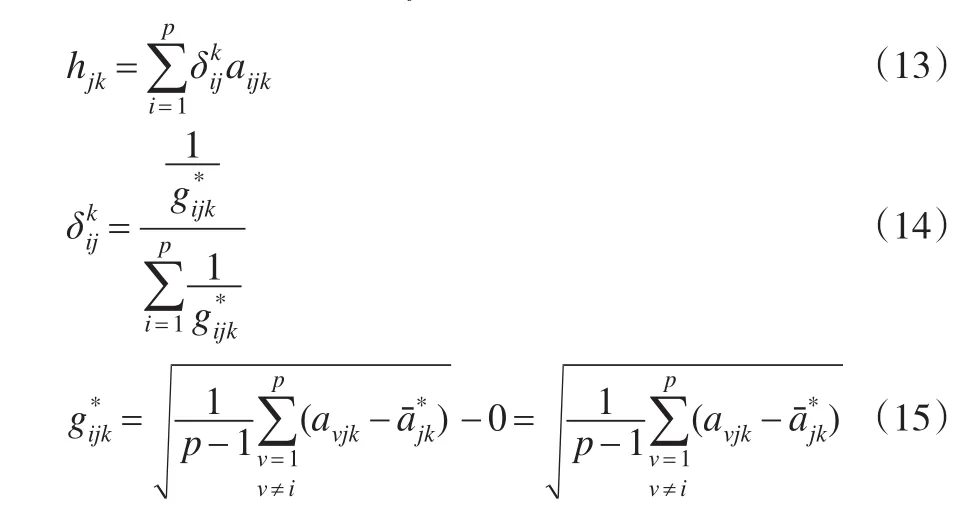
2.2.3 各评价者对指标信息矩阵中各元素的认知程度γijk的确定

γijk越大说明评价者sk对指标信息矩阵中的元素xijk的认知程度越高。
2.2.4 各评价者指标信息矩阵中同一元素下的评价者权重ωijk的确定。

集结信息为评价值时评价者权重ωik的确定。
将根据评价信息为各评价者的评价值时计算出的评价信息满意度矩阵(5)中的元素大小作为各评价者权重,并对其做归一化处理。

2.3 基于评价信息满意度的信息集结模型
当集结信息分别为指标信息和评价值时,根据上文计算出的评价者权重矩阵分别如下:

当评价信息为指标信息时的集结方式为:

当评价信息为评价值时的集结方式为:

2.4 基于评价信息满意度的信息集结方法的步骤
综合上面的讨论和分析,归纳出基于评价信息满意度的信息集结方法的步骤:
步骤1:请各评价者根据实际的评价问题给出评价信息,并对各评价者提供的评价信息做预处理。
步骤2:利用熵值法并根据式(1)至式(5)计算需要集结的评价信息的满意度矩阵Ak或E。
步骤3:当集结信息为指标信息时,根据式(6)至式(16)分别计算各评价者对各被评价对象和各评价指标从总体上的认知程度以及对指标信息单个元素的认知程度,并根据式(17)计算各评价者的权重矩阵Ωk。当评价信息为指标值时,则根据公式(18)计算评价者权重矩阵Ω。
步骤4:根据不同的集结信息,选择式(19)和式(20)对评价信息进行集结,得出群体信息最终的集结结果。
3 应用算例
本文选取文献[11]中的算例做参考(背景从略),共有4位评价者从10个极大型指标对4名教师进行评价并排序,其中10个评价指标的权重为ωi=(0.14,0.05,0.03,0.03,0.11,0.16,0.15,0.15,0.12,0.06),各评价者给出的指标信息(预处理后)如表3至表6所示。
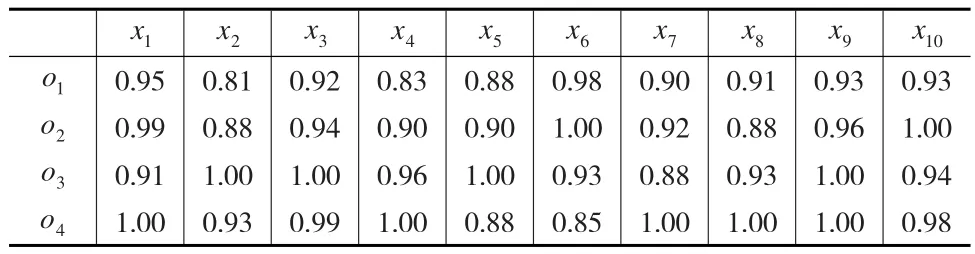
表3 评价者s1给出的指标信息
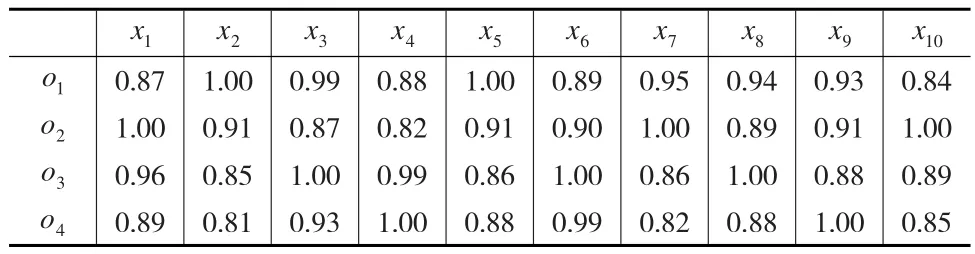
表4 评价者s2给出的指标信息
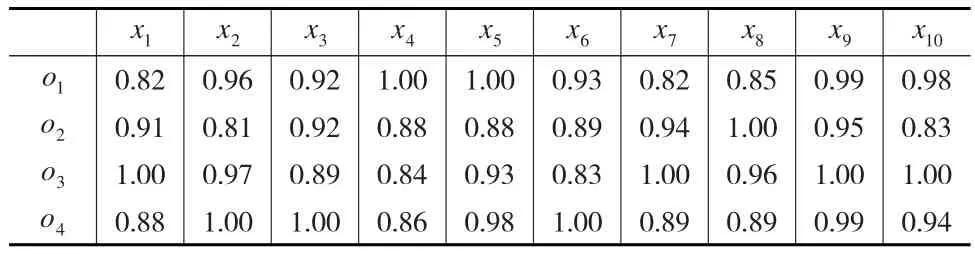
表5 评价者s3给出的指标信息
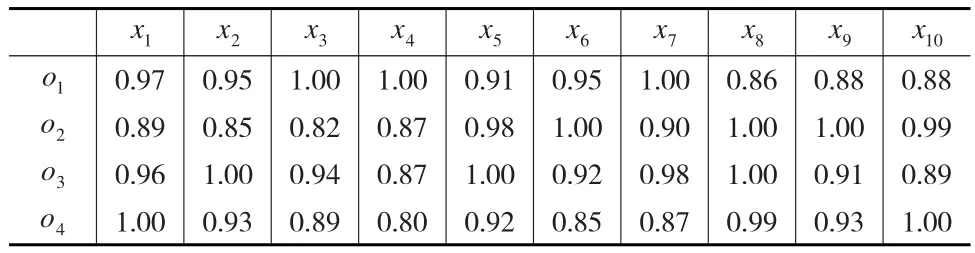
表6 评价者s4给出的指标信息
(1)根据式(1)至式(4)计算各评价者的指标信息满意度矩阵,其中参数c=0.5,计算结果见表7(为节省篇幅,仅列出评价者s1的计算结果)。

表7 评价者s1的指标信息满意度矩阵
(2)根据公式(6)、公式(11)、公式(16)及公式(17)计算各评价者的权重矩阵,其中λ1=λ2=0.5,计算结果如表8所示(仅列出评价者s1的计算结果)。
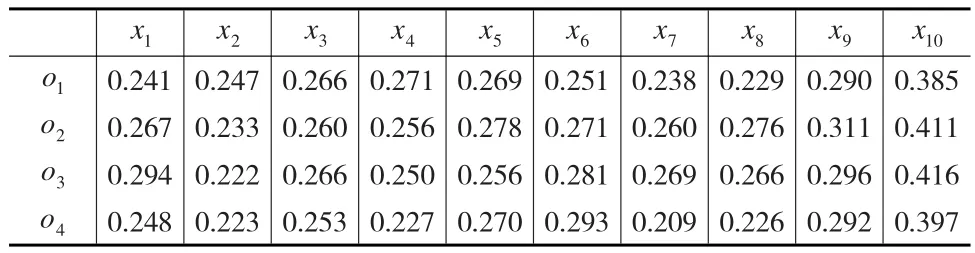
表8 评价者s1的权重矩阵
(3)根据式(19)得到最终的群集结结果如下页表9所示。
(4)根据OWGA算子对最终的群集结结果进行集结,得到各教师的群体综合评价值为Zi=(0.918,0.935,0.943,0.927),i=1,2,3,4。故最终的排序为o3≻o2≻o4≻o1,与文献[11]的排序结果o3≻o4≻o2≻o1明显不一样。本文采取的评价方法与文献[11]的方法相同,不同之处在于群体信息集结方法的选择,说明本文提出的群体信息集结方法对评价结果产生了影响,原因在于本文提出的信息集结方法赋予评价者的是一组权向量,而不是唯一的评价者权重,在评价的过程中考虑的信息更加全面,有效地避免了信息集结过程中不公平现象的产生,从而得到的结果更准确也更容易被接受。本文提出的集结方法对评价信息为指标值的情况同样有效,由于篇幅限制,算例从略。
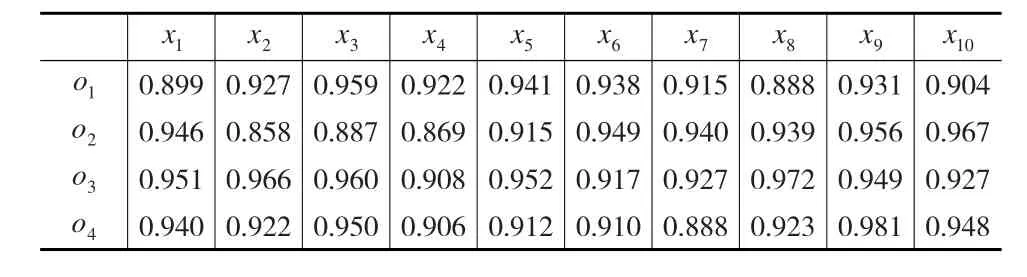
表9 最终的群集结结果
4 结束语
本文针对群体评价中不同评价信息集结的问题,综合考虑各评价者提供的评价信息的满意程度,提出了一种基于评价信息满意度的群体信息集结方法,该方法具有以下特征:(1)本文提出的方法改变了以往研究中评价者权重不变的思想,避免以固定的权重代表评价者提供所有信息的重要程度的弊端,而是针对不同的评价信息赋予评价者一组权重;(2)考虑的信息更加全面,文中评价者的权重综合考虑了各评价者对评价指标,被评价对象以及单个评价元素的认知情况,使集结结果更易接受;(3)本文提出的方法可以为以后评价活动中评价者的选择提供参考。最后通过实例的计算表明,该群体信息集结方法更加贴近现实,便于理解和推广。该方法可普遍适用于由多个评价者参与、且各评价者独立给出判断信息的群体评价活动中,如教师晋升评选中的专家打分等问题的处理。

