考虑贮料-钢板筒仓相互作用的静动态侧压力模拟研究*

戴士博 静行，2 郭旭 欧阳德光

1.河南工业大学土木工程学院 郑州450001

2.河南省现代绿色生态仓储体系国际联合实验室（河南工业大学） 郑州450001

引言

粮食钢板筒仓作为储存粮食的一种薄壁圆柱壳体结构，具有轻质高强、仓储容量大、易于机械化操作等优点，显示出良好的发展前景［1］。但这类仓储结构由于内部贮料的质量远大于结构自重，故在钢板筒仓的设计中也存在许多特殊问题，如几何尺寸和支撑形式、贮料力学特性、贮料与仓体复杂的相互作用及不同类型荷载作用的影响［2］。其中，仓内贮料对仓壁产生的侧压力是筒仓结构受力分析与设计的关键问题［3］，且目前各国筒仓结构设计规范对于侧压力的计算差异较大［4，5］。因此，有必要对贮料-筒仓结构体系的侧压力分布规律进行深入研究。

目前，通过建立精细化的有限元数值模型进行筒仓结构受力分析已成为该类研究的主要手段。张翀等［6］对地震作用下贮料的侧压力进行了研究，结合有限元数值模型提出了一种便于实际工程采用的筒仓侧压力计算方法。Mehretehran［7］等利用Drucker-Prager 模型模拟仓内贮料，对不同高径比的筒仓模型侧压力进行模拟，结果表明，有限元计算结果与经典Janssen 理论预测的压力分布吻合较好。杨鸿等［8］采用Drucker-Prager

模型描述贮料的本构关系，建立了考虑贮料与筒仓相互作用的有限元数值模型，进行了参数的拓展分析，讨论了贮料泊松比、内摩擦角、膨胀角及贮料与仓壁摩擦系数对侧压力的影响。Herle［9］等认为颗粒材料的应力-应变关系可以用亚塑性模型来描述，并对模型参数的确定方法进行了研究。周长东［10］等基于亚塑性本构理论对贮料的静态压力作用进行有限元模拟，提出贮料侧压力受初始孔隙比、内摩擦角、颗粒硬度和摩擦系数影响较大。

综上，为准确计算贮料-钢板筒仓结构体系的静、动态侧压力，本文采用亚塑性模型描述仓内贮料的力学行为，利用ABAQUS软件建立考虑散-固耦合效应的有限元数值模型，研究浅仓及深仓模型在自重和地震作用下的贮料侧压力分布，并将分析结果与中国、欧洲规范进行对比，以期明确粮食贮料-钢板筒仓结构体系静动态侧压力的分布规律。

1 亚塑性本构模型

亚塑性本构理论是一类新型的散粒型土体本构模型理论，其基本思想由德国学者Kolymbas［11］提出。它不是从弹塑性理论发展而来，没有屈服面、流动法则、硬化定律以及把应变分解为弹性和塑性部分等概念，而是以连续介质力学为基础，以张量函数为运算工具，将应力速率描述为应力、应变速率和孔隙比的函数，主要用于描述砂、碎石等无黏性散粒型土体的非弹性和非线性等主要力学特性。1996 年，Gudehus 和Wu等［12，13］提出了率的相关方程，随着研究的深入，von Wolffersdorff［14］对模型提出改进，应用于单元试验的模拟，并将数值计算与砂土试验结果进行对比，结果表明该模型很好地反映了颗粒材料的非线性特性，但应用于预测小振幅的循环应力或变形时，存在小应力循环下散粒体材料的变形过度累积的棘轮效应。为了能够正确反映土体在小变形范围内的变化，消除棘轮效应，Niemunis和Herle［15］基于von Wolffersdorff 提出的本构模型，引入了考虑颗粒间应变的概念，对模型进行进一步优化。

von Wolffersdorff 修正后的亚塑性本构模型如下：

式中：φc为材料临界摩擦角。

特征孔隙比为：

向密性函数fe、fd的表达式为：

正压性函数fb的表达式为：

式中：hs为颗粒硬度；n 为hs与所对应的参数；α、β为确定三轴试验中内摩擦角峰值的相关参数；ei、ec和ed分别为颗粒材料的上限孔隙比、临界孔隙比和下限孔隙比。

由式（1）～（9），von Wolffersdorff 亚塑性本构模型共需要8 个参数：颗粒硬度hs；临界摩擦角φc；在零压状态下颗粒材料的最大孔隙比ei0、临界孔隙比ec0和最小孔隙比ed0；参数n、α、β。

为了消除在小应力循环下散粒体材料变形过度积累的棘轮效应，Niemunis 和Herle［15］基于von Wolffersdorff修正的8 参数本构模型，补充5个材料参数描述材料在荷载逆转后的刚度变化：R、mR、mT、βr、χ。其中，参数R 定义了颗粒间应变的范围；参数mR、mT定义了在应变空间内，应变路径出现90°和180°负载时对应于0°的刚度变化；参数βr、χ 用于对刚度的变化进行平滑处理。

2 数值模型建立与合理性论证

钢板筒仓中的贮料是由颗粒组成的带有空隙的集合体，其动力学行为具有固体和液体双重特性。本文采用亚塑性模型来表征小麦粮食散体贮料的本构模型，综合考虑了散料的初始孔隙比、颗粒硬度及颗粒间应变的影响，具体材料参数见表1［16］。其中，筒仓仓壁采用4 结点双曲线薄壳单元（S4R）建模，贮料采用8 结点三维实体单元（C3D8）模拟。筒仓仓壁、筒仓底部和筒仓内颗粒材料之间的界面由ABAQUS 中提供的“接触对”算法建模。将筒仓仓壁和仓底表面视为主表面，将与筒仓仓壁和仓底接触的颗粒材料外表面视为从表面。二者之间的摩擦模型选用库仑模型，摩擦系数设定为0.3［4］。对于接触约束，考虑了“罚”接触算法，这类似于在主从表面之间引入刚性弹簧以防止从面穿透主面。为减小误差，模型中壳单元与实体单元表面的网格划分为一一对应的关系。

表1 亚塑性模型参数Tab.1 Parameters of the hypoplastic model

为了验证以上建模方法的有效性，采用该数值模拟方法对既有筒仓模型试验［17，18］进行建模分析。该试验模型为落地式圆形钢板筒仓，钢材型号为Q235，筒仓直径为800mm，高度为900mm，仓壁厚度为1mm，试验过程中，仓壁始终处于弹性状态，故考虑钢板筒仓为弹性体进行建模计算。

将模拟计算结果与试验数据进行对比如图1所示，不同测点位置处的数值模拟结果与试验结果的最大误差均在15%以内，且二者的分布趋势基本一致，由此表明亚塑性本构模型可以较好地描述小麦贮料的力学行为，从而验证了利用该建模方法分析贮料筒仓结构体系侧压力的合理性。

图1 筒仓仓壁侧压力试验值与模拟值对比Fig.1 Comparison of experimental and simulated values of silo wall lateral pressure

3 粮食钢板筒仓模型建立与结果分析

3.1 模型建立

中国规范根据筒仓高径比的不同，将筒仓划分为浅仓和深仓；欧洲规范划分为储存仓、粗矮筒仓、中等细长筒仓和细长筒仓，具体划分标准见表2［4，5］。基于上述建模方法，建立浅仓（H／D ＝1.2）和深仓（H／D ＝1.8）两种有限元模型，浅仓模型高6m，深仓模型高10m，直径均为5m，厚度0.02m。对模型施加竖直方向上的重力荷载。重力分析完成后，对筒仓底部沿X 方向输入Elcentro地震波，采用隐式动力分析，地震波总持时为20s，时间间隔为0.02s，参考《建筑抗震设计规范》［19］设计基本地震动峰值加速度，将输入峰值地面加速度PGA分为0.05g、0.1g、0.2g和0.3g四个等级，其中0.05g对应较小地震烈度工况，0.1g和0.2g 对应中等地震烈度工况，0.3g对应较强地震烈度工况（表3）。图2 为贮料-钢板筒仓结构体系模型的网格划分，其中壳体单元与实体单元的表面网格划分为一一对应关系。

图2 有限元模型的网格划分Fig.2 Meshing of the finite element model

表2 不同规范的筒仓分类Tab.2 Classification of silos with different specifications

表3 多遇、设计基本、罕遇地震加速度值Tab.3 Earthquake acceleration values for multiple，basic design and rare intensities

3.2 静态侧压力

对于浅仓而言，中国规范基于Rankine 理论提出贮料侧压力的设计计算公式；而对于深仓侧压力的计算，两国规范都以基于连续介质模型的Janssen理论为基础，但侧压力系数k的取值不同。

中国规范规定不同筒仓类型计算深度为s处的贮料静态压力标准值方法如下［4］：

式中：k ＝tan2（45° -φ／2）为侧压力系数；γ为贮料的重度；μ为贮料对仓壁的摩擦系数；ρ ＝dn／4为筒仓净截面的水力半径。

欧洲规范对筒仓类型的划分不同于中国规范，本文所建立的有限元数值模型属于中等细长筒仓，对于填充结束时任意深度z处的水平压力计算方法如下［5］：

式中：K ＝1.1（1-sinφ）为侧压力系数；n ＝-（1 +tanφ）（1 -h0／z0）；h0为粮堆锥面重心到锥底的垂直距离；z0为Janssen深度特征值；A为筒仓横截面面积；U为筒仓横截面周长；YR为筒仓压力深度变化函数。

图3 为仓内贮料的Mises 等效应力云图。可以发现，沿筒仓深度变化，各筒仓模型贮料的应力分布均表现出一定的非均匀性。同一深度面处，靠近结构顶部的贮料应力分布较为一致，最大应力位于贮料底部位置，且呈现出“中心大，四周小”的趋势。深仓模型较浅仓模型更为明显，这表明随着装粮高度的增加，受粮食拱效应的影响，贮料内部应力分布的非均匀性更为显著。

图3 仓内贮料Mises 等效应力云图（单位：Pa）Fig.3 Mises equivalent force cloud of the silo storage material（unit：Pa）

如图4 所示，将有限元模拟结果与两国规范计算所得不同深度位置处静态压力标准值进行对比分析。可以发现，浅仓模型与深仓模型侧压力的数值模拟结果均与中国规范计算所得侧压力标准值的分布趋势吻合较好，这也进一步验证了所建立有限元数值模型的合理性。

图4 筒仓静态侧压力分布Fig.4 Static lateral pressure distribution of silos

由图4 可以看出，对于浅仓模型，根据中国规范计算所得设计侧压力的分布趋势更接近于模拟结果，计算值较有限元结果最大高出16.5%，具有足够的安全储备，表明中国规范采用Rankine理论对浅仓模型进行侧压力设计是合理的，而欧洲规范则过于保守；对于深仓模型，根据欧洲规范计算所得的设计侧压力明显大于中国规范和数值模拟的结果，原因在于中国规范与欧洲规范贮料侧压力计算所采用的基本理论虽然相同，但两国规范选取侧压力系数不同，使得两种规范计算所得的贮料侧压力存在较大差别。中国规范计算设计值与模拟值差距较小，但模型底部的模拟值比规范值高11.2%，反映出有限元数值模拟计算时，筒仓底板对仓壁底部约束的增强，使得筒仓仓壁底部的刚度较顶部位置发生突变而产生应力集中现象，从而模型底部位置的侧压力显著增大，而规范中并未考虑筒仓底部约束效应的影响。文献［9］指出伴随着筒仓高度的进一步增加，此部分差值可能会更大，故对中国规范侧压力系数的取值应适当增大。

3.3 动态侧压力

除静态侧压力外，粮食散体在地震作用下会对仓壁产生额外的附加法向压力（相对动态侧压力）。欧洲规范中提出了对地震作用下圆形筒仓仓壁粮食散体产生的动态侧压力的估算方法［20］：

式中：Δph，so为基准压力；θ 为筒仓壁相关点对应的径线与地震作用水平分量方向之间的角度（0°≤θ ＜360°）。

在离仓底垂直距离为x 处筒仓壁的各点上，基准压力Δph，so可取值为：

式中：α（z）为离贮料等效面的垂直距离为z处的筒仓反应加速度与重力加速度之比；γ 为贮料的重度；＝min（hb；dc／2），hb为筒仓的总高度；dc为与筒仓的内径。

图5 为浅仓模型和深仓模型在不同PGA作用下沿筒仓高度变化的相对水平动压力包络。由于在对模型进行动力分析前的分析步中考虑了各筒仓模型整体的自重作用，因此，为了得到动态侧压力包络图，首先计算各测点的动压力时程，再用重力分析步末的压力值减去动压力时程，最后将各测点动压力最大值作为动压力的包络值。

图5 筒仓动态压力分布Fig.5 Dynamic pressure distribution of silos

从图5 可以直观看出，不同PGA作用下，浅仓模型与深仓模型的相对动态侧压力变化趋势相同，均随着PGA的增大而逐渐增大，但浅仓模型的相对动侧压力沿筒仓高度变化较为均匀。在小震与中震区间内（PGA 为0.05g 与0.1g），浅仓和深仓模型最大相对动态侧压力均出现在结构的中上部区域，而顶部较小；随着地震动强度的增加（PGA为0.2g与0.3g），深仓模型相对动侧压力峰值出现的位置较浅仓模型显著提高，且计算所得动态侧压力最大值较浅仓模型分别增大了1.2 倍和2.4 倍。由此可见，PGA 与高径比的变化对贮料筒仓结构体系动侧压力分布影响较大；相同PGA作用下，浅仓模型下部的相对动态侧压力值要略高于深仓模型。原因在于，随着高径比的增大，仓内充填贮料随之增多，此时上部贮料在自重作用下对中下部贮料的压实作用显著增大，故在地震作用下，深仓模型中下部的贮料与仓壁更趋于整体运动，贮料对筒仓仓体的碰撞冲击作用低于浅仓模型；值得注意的是，贮料最大相对动态侧压力并不在顶部位置产生，而是在模型的中部及中上部附近位置。这是由于在地震作用下，贮料顶部为自由区域，可以沿水平及垂直方向运动，而中间位置受到上部及下部贮料的双重约束，故此时对筒仓侧壁的碰撞及冲击会较顶部更为剧烈。

图6 为浅仓及深仓模型最大相对动态侧压力平均值（图5 中压力分布的平均值）与根据欧洲规范计算所得平均值的对比。

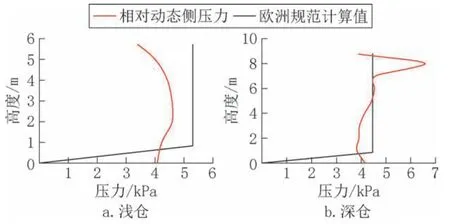
图6 平均相对动态侧压力分布与欧洲规范的对比Fig.6 Comparison of average relative dynamic lateral pressure distribution with eurocode

从图6 中可以看出，靠近筒仓底部附近，欧洲规范建议的动压力值并不保守，这与文献［21］所得结果一致。除了底部位置外，浅仓模型的动压力包络均低于欧洲规范建议的压力值；而对于深仓模型，靠近结构顶部位置处相对动态侧压力分布具有显著的放大效应，最大相对动态侧压力超出欧洲规范计算建议值的47%。这说明，对于浅仓模型，欧洲规范给出的建议是合理的；在深仓模型中，由于仓内贮料对筒仓仓壁的碰撞及冲击，欧洲规范假设α（z）为恒定值（不考虑加速度响应沿结构高度的变化）并不合理。

4 结论

本文采用亚塑性本构模型描述仓内小麦贮料的力学行为，基于ABAQUS有限元软件建立了考虑贮料与仓体相互作用的钢板筒仓有限元数值模型，研究了浅仓和深仓模型贮料静动态侧压力的分布规律，并将分析结果与中国及欧洲规范进行对比分析，得出以下结论：

1.钢板筒仓贮料静动态侧压力有限元模拟结果与实仓模型振动台试验结果吻合较好，表明利用亚塑性本构模型可以较为准确地描述仓内小麦贮料的力学行为，同时也验证了所用建模方法的合理性。

2.自重作用下，贮料内部应力分布具有明显的非均匀性，最大应力位于筒仓底部，且同一水平面应力分布呈现出“中心大，四周小”的趋势；计算所得浅仓和深仓模型静侧压力均与中国规范吻合较好，Rankine 理论可以较为准确地计算浅仓静侧压力；欧洲规范由于侧压力系数偏大导致计算结果过于保守。

3.同一地震强度下，深仓模型底部附近相对动态侧压力较浅仓模型略有降低，随着地震动强度的增加，浅仓模型的相对动侧压力沿筒仓高度变化较为均匀，而深仓模型在大震作用下仓顶附近的相对动侧压力分布具有较大的放大效应；欧洲规范建议的浅仓动压力分布具有一定的保守性，而深仓动压力计算中有关加速度响应沿结构高度变化恒定的假设并不合理。