箱形基础在火电厂塔式锅炉中的运用及计算分析

葛小丰 黄小玲 葛新峰 张建军

中国能源建设集团江苏省电力设计院有限公司 南京210024

引言

世界上大容量机组的锅炉主要有Π型和塔式两种炉型。相较而言，塔式炉在燃用易结焦的煤质、减轻烟温偏差、受热面磨损、启动疏水等方面存在结构性优势。目前，国内最先进的1000MW超超临界二次再热机组锅炉大多选用塔式炉。

1000MW机组塔式炉高度超过100m，其巨大的本体荷载大部分支承在锅炉构架核心钢柱上，桩基是最常用的基础结构方案。本文根据某工程的地质特点，提出了塔式炉核心承重柱采用箱形基础的方案，并计算论证其适用性。

1 工程背景及箱形基础方案确定

1.1 工程外部条件

某工程项目建设2 ×1000MW 超超临界二次再热燃煤发电机组，厂址位于江苏省连云港市。厂区的地基岩土上部主要由人工填土、第四系全新统冲积、湖积及海滨相沉积土层和第四系中、上更新统冲积、湖积、洪积及坡积土层组成，下部由前震旦系锦屏组花岗片麻岩组成。岩土设计参数见表1。厂址抗震设防烈度为Ⅶ度，建筑场地类别为Ⅱ类，设计地震分组为第三组。地震安评报告提供的参数见表2。

表1 岩土设计参数Tab.1 Geotechnical parameters for design

表2 抗震设计参数Tab.2 Seismic parameters for design

厂址50 年一遇的基本风压为0.55kN／m2，100 年一遇的基本风压为0.65kN／m2。

1.2 箱形基础方案的确定

根据锅炉厂家提供的资料，每座塔式锅炉总荷重约570000kN（标准组合），其中大部分荷载由4根2.5m×2.5m的箱形核心钢柱承担，这4根柱的柱网尺寸为30.5m×31.5m。通常情况下塔式炉基础多采用桩基承台方案，由于本工程浅层深度内分布承载力较高的土层，故对采用天然地基箱形基础方案与桩基承台方案进行详细的分析对比。

桩基承台方案要素简述如下：桩型采用C40人工挖孔灌注桩，桩长约15.6m，持力层为⑥，桩径1000mm。桩基方案布置见图1。为满足承载力的要求，上述4根箱形钢柱对应的基础灌注桩采取了扩孔+后注浆措施，单桩承载力的计算及相关技术要求按文献［1］执行，结果见表3。

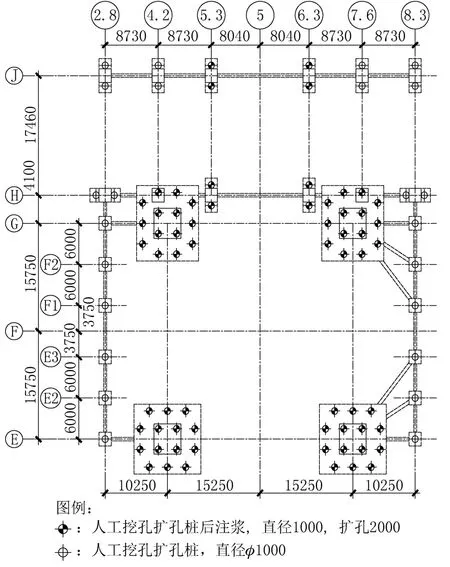
图1 桩基方案Fig.1 Pile foundation layout plan

表3 灌注桩承载力（单位：kN）Tab.3 Bearing capacity of cast-in-place piles（unit：kN）

箱形基础方案采用天然地基，持力层为④，其布置方案见图2。两种方案的经济技术对比见表4、表5，可见两个方案经济性基本持平，在技术上箱基方案更具优势。鉴于建设方对项目开工日期（以浇第一罐混凝土为标志）和总工期有要求，因此塔式炉最终采用了天然地基的箱形基础方案。

图2 箱形基础方案Fig.2 Box foundation layout plan

表4 锅炉基础方案经济对比（一台炉）Tab.4 Economic comparison of boiler foundation（One Boiler only）

表5 锅炉基础方案技术对比Tab.5 Technical comparison of boiler foundation

2 塔式炉箱形基础的计算与分析

2.1 箱基初步方案

箱形基础平面尺寸41.06m ×44.4m，箱基高度取6.5m，参照文献［3］规定，箱基中间隔墙水平截面总面积大于1／10 的基础底面积，同时平均每平方米面积上的墙体长度大于0.4m，箱基平、剖面见图3。

图3 箱形基础平、剖面Fig.3 Sketch of box foundation section

2.2 分析方法与分析重点

采用大型有限元软件AYSYS 为工具，对箱型基础方案的地基和基础统一建模进行有限元法分析，参考文献［5］、［6］，土层及箱基本体均采用六面体实体单元模拟，基础采用线弹性本构模型；土层则按线弹性和弹塑性本构模型分别建模，土层弹性模量直接使用压缩模量，并根据沉降经验系数进行修正；为考虑开挖部分土体自重及水浮力对沉降和承载力计算的影响，在箱形基础底板顶面生成表面效应单元，用于施加水浮力及开挖土体自重形成的上托力。

为验证有限元法的合理性，采用倒楼盖法、BOX软件计算法进行对比分析。倒楼盖法假定地基反力按弯矩作用下的梯形荷载作用于底板，将顶板、底板作为一定宽度的翼缘和墙组成工字形混凝土梁，采用PM建模、SATWE计算，该方法最简单但同时也是最粗略的。

倒楼盖法沉降计算采用布辛奈斯克附加应力模型，可采用文献［7］给出的分层总和法公式计算：

式中：s1为基坑回填再压缩沉降量；s2为基底附加应力的沉降量；ψ'、ψs分别为回弹沉降经验系数和沉降经验系数；Esi取Es1-3。

BOX法采用箱基设计软件，参考文献［4］，选择底板刚性假定计算地基反力，各分块的柔度系数ξij计算采用压缩层分层的地基模型，其中地基模型系数Kij取0.35。

选取锅炉厂提供的炉架柱脚恒、活、风、震参与组合的最大轴力标准组合工况作为计算比较荷载。计算分析的重点包括沉降变形、地基承载力、箱基的整体弯矩、箱基主梁（隔墙）的弯矩及剪力分布，以进一步探究结构方案的适用性和合理性。

2.3 分析结果

1.地基沉降计算与对比

有限元法计算时，土体分别采用弹性和弹塑性建模，二者的沉降计算值差别不大，见图4。

图4 箱基沉降云图（单位：mm）Fig.4 Foundation settlement（unit：mm）

有限元法计算的沉降未考虑基坑回弹再压缩沉降，且计算结果需要按沉降经验系数进行修正。根据经验和计算，取沉降经验系数ψs＝0.45。线弹性土体模型修正后角点最大沉降约为38mm，中间最大沉降约为27mm。

倒楼盖法采用公式（1）～（3），根据经验取Es1-3＝（1.1～1.2）Es1-2、ψ' ＝1.0。ψs同有限元法，取0.45。沉降计算结果如下：中心点沉降s ＝81.5mm（其中s1＝16.5、s2＝65）、角点沉降s ＝23.7mm（其中s1＝4.2、s2＝19.5）。

BOX法由于采用刚性底板假定，整体地基沉降均为25mm，该值同样未考虑基坑回弹再压缩。

建设及运维期间中对锅炉的4 个钢柱及箱形基础顶面所设的沉降标进行了长期观测，结果如图5 所示。

图5 沉降观测数据Fig.5 Settlement observation data

以上沉降计算及实测结果对比见表6。由表6 可见，三种方法计算出的沉降值特点有显著差异：有限元法反映了土体和基础的实际刚度影响，沉降呈现角点大、中心小的特点；BOX法由于假定基础底板为刚体，导致角点与中心沉降一致；倒楼盖法由于假定基底反力梯形分布，导致角点沉降小、中心沉降大。

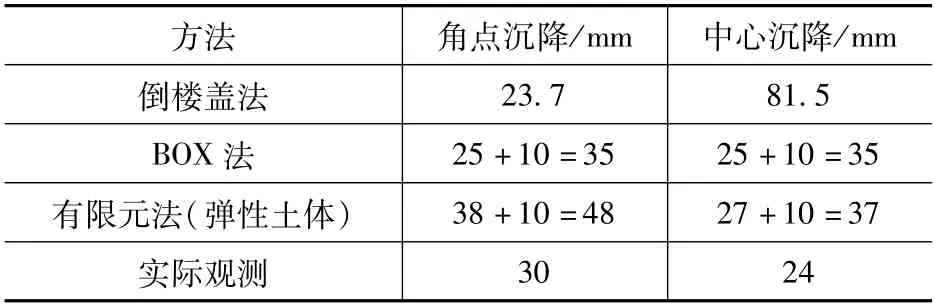
表6 沉降数据对比汇总Tab.6 Summary of settlement data

实测数据体现的沉降值分布特点与有限元法基本一致，但数值偏小，其原因是沉降计算过程中涉及到的ψs为半经验值，另外地基参数、土层分布、实际荷载等与计算输入可能存在一定差异。

总体而言，有限元法计算的地基沉降分布特点相对于其他算法与实测更加吻合，结果偏于安全，且总沉降量和沉降差（包括锅炉本体柱间及锅炉与主厂房之间）满足文献［2］的相关要求。

2.地基承载力验算与对比

有限元法计算所得土体线弹性和弹塑性条件下的应力见图6。图7 显示了箱基中间横向（图3的1-1 剖面）和箱基中间纵向（图3 的2-2 剖面）分别用s-x和s-y表示得出的有限元法地基反力断面图。

图6 地基反力云图（单位：MPa）Fig.6 Foundation reaction（unit：MPa）

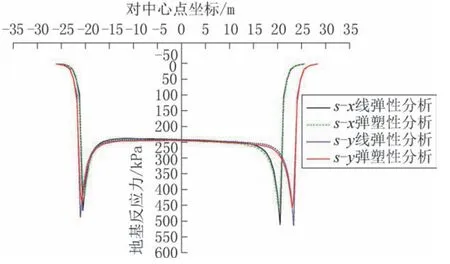
图7 有限元分析地基反力分布断面Fig.7 The section of foundation reaction by finite element analysis

倒楼盖法、BOX法和有限元法计算的地基反力结果见表7。由表7 所示：倒楼盖法假定箱形基础为一个完全刚体，地基反力呈现弯矩作用下的梯形平面分布；BOX法和有限元法地基反力分布都呈现出四边大、中间小的特点，这与文献［7］附录E的地基反力系数趋势上是一致的，但有限元法显示的边、中差距更为突出，反力数值的收敛比文献［7］及BOX法更为迅速，且收敛后很快进入平段；另外，有限元法结果显示基础外周土体并非零应力，而是承受了一定的荷载，这也使得箱基平面内有限元法的地基反力平均值相对其他两种计算方式略小。

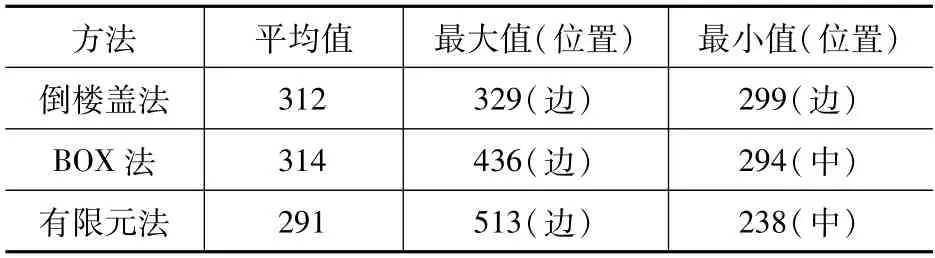
表7 地基反力计算结果（单位：kPa）Tab.7 Results of foundation reaction（unit：kPa）

倒楼盖法没有考虑地基应力、应变的协同；BOX法通过将箱基底板划分为许多区格，建立各区格应力和位移协同方程，并通过地基模型系数Kij来考虑土的应力、应变扩散能力后的折减系数，但Kij取值为经验值；有限元法相对于BOX法，在单元划分上更为精细，能更加准确地考虑土-基础的协同变形和受力，沉降计算结果和实测的对比也验证了这一点。因此，采用有限元法计算的地基反力结果来验算地基承载力更为合理。

地基承载力允许值按文献［8］如下公式计算：

式中：基础的深度修正系数ηd＝1.6；宽度修正系数ηb＝0.3；基础宽度取b ＝6m。修正后的层④承载力特征值为422kPa，对应最大应力时取1.2 倍，为507kPa，该值略小于有限元法土体线弹性计算结果的最大应力513kPa，但大于土体弹塑性条件下的最大应力495kPa，因此地基承载力是满足要求的。

3.整体弯矩分析与对比

以1-1 剖面对应的整体跨中弯矩为对象进行分析对比。有限元法需要编制后处理程序，将应力导出为对应于截面中和轴的弯矩值；倒楼盖法的整体弯矩可以从SATWE 程序输出文件中的构件弯矩图叠加取得；BOX法计算整体弯矩，文献［4］提出了弹性交叉梁系和整体静定梁两种方法，塔式炉高度大，横向刚度主要通过钢支撑提供，不满足弹性交叉梁系法上部结构刚度大而且布置规则的假定，因此选择整体静定梁法。

有限元法与BOX 法构件定义一致，对构件的定义为墙和板，墙指顶、底板间的竖向构件，相当于倒楼盖法工字形混凝土梁的腹板。有限元法得到的墙X 向正应力云图见图8a（Y 向相似，不再赘述）；另在1-1 剖面中间350 厚墙两侧取截面分析顶、底板的拉、压力（该处整体Mx最大），对应的正应力云图见图8b。

图8 正应力云图（单位：MPa）Fig.8 Normal stress（unit：MPa）

BOX法的整体静定梁法主要原理为：整个箱基在X、Y方向上分别计算各截面的弯矩和剪力，其中剪力由箱基的横墙或纵墙承受，弯矩一部分转化为墙的受弯，另一部分转化为顶、底板的拉、压力，计算简图见图9a，整体弯矩输出见图9b。

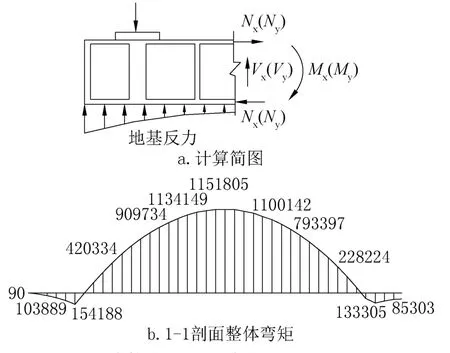
图9 整体静定梁法整体弯矩（单位：kN·m）Fig.9 Overall bending moment value（unit：kN·m）

图8a显示有限元法计算的箱基墙体最大正应力在剖面的中部，与图9b 所示弯矩图一致；图8b显示有限元法计算的箱基底板全程受压、顶板全程受拉，这与图9a 所示的BOX 法整体静定梁的计算假定也是吻合的。

整体弯矩计算的结果为：有限元法1009026kN·m、BOX法1151805kN·m、倒楼盖法1020403kN·m。三种算法的整体弯矩结果与前节所述基底反力特点是相对应的：有限元法由于基底反力从四周向中间很快收敛到接近平均值，因此计算值和倒楼盖法基本接近；BOX法由于基底反力收敛到平均值的速度相对较慢，且箱形基础偏中部的地基反力比有限元法大，因此跨中总体弯矩相较于有限元法略大。

箱型基础的整体弯矩分析对比表明，有限元法所揭示的受力特性是符合对比算法BOX 的基本假定的；其数值与基底反力相对应，也是合理的。

4.主要构件内力计算与对比

除了整体弯矩以外，还需要对墙体承担的弯矩（图9a中的Mx、My）分担比例进行比较，由于倒楼盖法构件定义的不同，分担比例的比较仅BOX法和有限元法参与。两种方法墙体分担弯矩见表8。

表8 箱基典型截面整体弯矩及墙分担弯矩对比（单位：kN·m）Tab.8 Overall bending moment and wall shared bending moment（unit：kN·m）

在墙体分担弯矩比例上，BOX法墙体的弯矩占总比例的31%，而有限元法只占21%，说明有限元法箱基顶、底板承受了更大的拉、压力，翼缘作用更加明显。

在抗剪承载力方面，图10 为有限元法计算的墙xz向剪应力云图，可见剪应力最大的是四根连结柱墩的1.7m 宽墙体（yz 向相似，不再赘述）。

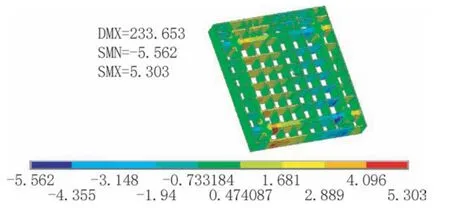
图10 xz 向墙体剪应力云图（单位：MPa）Fig.10 xz direction wall shear stress（unit：MPa）

以4.2-E轴的柱墩为例，BOX法和有限元法1.7m宽墙端剪力计算结果对比见图11。

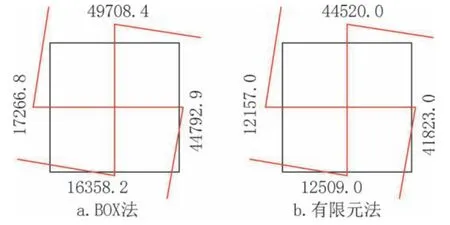
图11 墙端剪力对比（单位：kN）Fig.11 Wall end shear force（unit：kN）

在剪力总值上，BOX 法比有限元法多约13%；在剪力分配上，BOX法外侧悬挑的墙剪力分配比例比有限元法大，而内侧连接柱墩的墙分配比例比有限元法小。主要原因是有限元法地基、基础整体建模计算，柱墩截面范围内的地基反力抵消了一定的上部荷载（即总剪力），另外两者地基反力收敛特性的不同也对剪力总值和分配比例有一定的影响。

虽然有限元法计算结果从理论上分析更为精确，但基于BOX 法揭示的薄弱部位，在实际方案应用时，建议对隔墙的顶、底部增加纵向配筋，并在柱墩连接隔墙的的端部采取箍筋加密措施，确保基础的薄弱部位得到有效加强。

3 结论

1.在承载力合适的地基上，塔式炉采用箱形基础是可行的，而且在结构整体稳定性和协同主厂房沉降差方面具有优势；

2.塔式炉采用箱形基础受力比较复杂，需要进行详细的计算分析，各种方法计算结果对比表明，采用有限元法进行数值分析是合理、可靠、准确的设计手段；

3.箱形基础的塔式炉实际投产运行良好，实测沉降小于有限元法计算值，但沉降分布规律与实测吻合较好；

4.塔式炉箱形基础的地基反力有限元分析结果呈现出四周大、中间小的锅底状，且收敛速度比规范给出的参考值更为迅速；

5.由于塔式炉核心受力柱间距大，箱形基础明显表现出整体受弯的特性，连接柱墩的顶、底板及主墙体是受力的薄弱环节；

6.本文仅对最大轴力组合进行了整体及主要构件的分析，其他荷载工况及构件对应的计算在实施过程中需要进一步细化，以确保结构的安全可靠。