地下装配式大直径组合筒仓仓壁稳定性分析

张 昊 王馨康 谌 磊

（河南工业大学土木工程（建筑）学院，河南 郑州 450001）

关键字：地下仓；稳定性分析；组合圆筒壳；等效屈曲；钢板-混凝土结构

0 引言

粮食安全事关国家安全。随着国内、国际形势的变化，我国对粮食储备安全和技术手段的要求也越来越高，而地下粮仓在节能节地、绿色环保、优质储粮等方面有着显著优势，是我国建立绿色储粮新体系的重要技术支撑，也是今后粮仓建设的发展方向之一［1］。预制装配式钢板-混凝土地下粮仓采用内衬钢板防水，实现结构防水受力一体化，同时可通过逆作法解决地下现浇组合结构土方工作量大、施工工期长的问题，如图1 所示。目前，地下装配式组合结构已应用于实际工程中［2-4］，但随着地下粮仓单仓储量的不断增大，仓体埋深和仓壁直径不断增加，如何对水土压力作用下的装配式组合仓壁稳定性进行验算，成为当前进一步推广装配式地下粮仓亟须解决的问题。

图1 预制装配式地下粮仓仓壁

装配式地下结构接头是影响结构整体受力性能的关键部位，国内外对类似地下结构进行了大量研究。叶亮等［5］对一种新型型钢-混凝土组合接头的抗弯性能进行试验研究；焦勇强等［6］总结了整体预制拼装式综合管廊常用的接头型式及防水构造的优缺点及适用范围，为综合管廊接头的设计与改进提供参考；Liu 等［7］通过试验和数值分析，对比采用预制侧壁节点与现浇侧壁节点的地铁车站在低周往复荷载作用下的抗震性能，为地下混凝土结构设计提出节点最优的形状和设置位置。在装配式地下粮仓方面，张昊等［8］对地下组合粮仓竖向接头的受弯性能进行研究，结果表明，接头处传力钢板与内侧止水钢板可共同发挥抗拉作用；王振清等［9］在装配式地下粮仓钢板-混凝土组合仓壁轴压试验的基础上进行非线性有限元分析，并给出组合仓壁轴压峰值荷载简化计算式。

综上所述，国内外对装配式地下组合筒仓仓壁稳定性研究较少，本研究对地下装配式钢板-混凝土仓壁在外表面均布荷载作用下的稳定性问题进行研究，为工程应用提供理论依据及设计参考。

1 有限元法分析

为验证有限元法计算地下仓仓壁屈曲荷载的可靠性，利用有限元软件Abaqus 建立大直径无接头混凝土仓壁数值模型进行线性屈曲分析。

地下仓在施工和使用阶段存在多种工况，在施工阶段，当预制的组合仓壁管片全部拼装完成，且还没有施工仓底漏斗和仓顶盖时为最不利工况。取地下粮仓仓壁最底部高度为1 m 的仓壁圆筒为研究对象，并近似认为空仓（最不利工况）时，仓壁承受的外侧径向水土侧压力为均布荷载，且不考虑仓底、仓顶对仓壁的约束作用。

建立地下仓壁的稳定性分析数值模型，以仓壁径向为X轴、环向为Y轴、高度方向为Z轴，建立空间柱坐标系。仓壁圆筒模型结构对称，外部压力荷载也对称，利用对称性建立半个圆筒有限元模型，仓壁模型的参数及尺寸见表1。经网格收敛性分析后，网格尺寸取为0.04 m、混凝土材料采用C3D8R实体单元。地下粮仓仓壁主要以受压为主，钢筋与混凝土在弹性受压阶段协同工作，将其视为一个整体，忽略线性屈曲分析中配筋对仓壁整体稳定性的影响。在仓壁模型两端截面施加对称面约束以限制在Y方向的位移和绕X轴、Z轴方向的转动，利用约束方程控制两个端面内侧节点在X方向的位移，在仓壁顶面和底面施加Z方向的位移约束，在仓壁模型外表面施加单位大小的径向均布荷载。

表1 地下组合仓壁数值模型参数

本研究使用Lanczos 法对250 mm 厚现浇混凝土仓壁进行屈曲分析，得到其特征值为48 575.3，即其屈曲荷载数值解为48.575 kPa，屈曲模态如图2所示。

图2 现浇地下钢板-混凝土仓壁屈曲模态

Timoshenko［10］给出径向均布荷载作用下单层圆筒壳屈曲荷载的表示，见式（1）。

式中：qcr为薄壁圆筒的屈曲荷载；E、I、μ分别为材料的弹性模量、截面惯性矩和泊松比；R为圆筒截面中心点到筒壁圆心的距离。

通过该公式可计算得到屈曲荷载理论解。屈曲荷载数值解与理论解的对比结果见表2，证明利用有限元法对地下组合仓壁进行屈曲分析是准确、可靠的。

表2 现浇混凝土仓壁屈曲荷载

2 装配式地下筒仓仓壁稳定性分析

为进一步研究在大直径装配式地下组合仓壁设计中接头刚度对仓壁整体稳定性的影响，对内径为25 m、径厚比为100∶1 的装配式组合仓壁进行分析。

2.1 接头设计

装配式钢板-混凝土组合仓壁预制构件通过竖向接头连接成环，考虑实际工程需求，本研究设计的喇叭形竖向接头如图3 所示。该接头由钢桩、外侧包边钢板、腹板、内侧包边钢板、止水钢板、外侧包边延伸钢板组成。喇叭形开口方便施焊，同时接头空腔内可灌注防水材料，与钢桩翼缘板、止水钢板组成三道防水层。其中，内侧包边钢板、外侧包边钢板与腹板厚度为20 mm，外侧包边延伸钢板厚度为5 mm，钢桩翼缘板与止水钢板厚度为t0，通过调整t0的大小可控制接头抗弯刚度的大小。

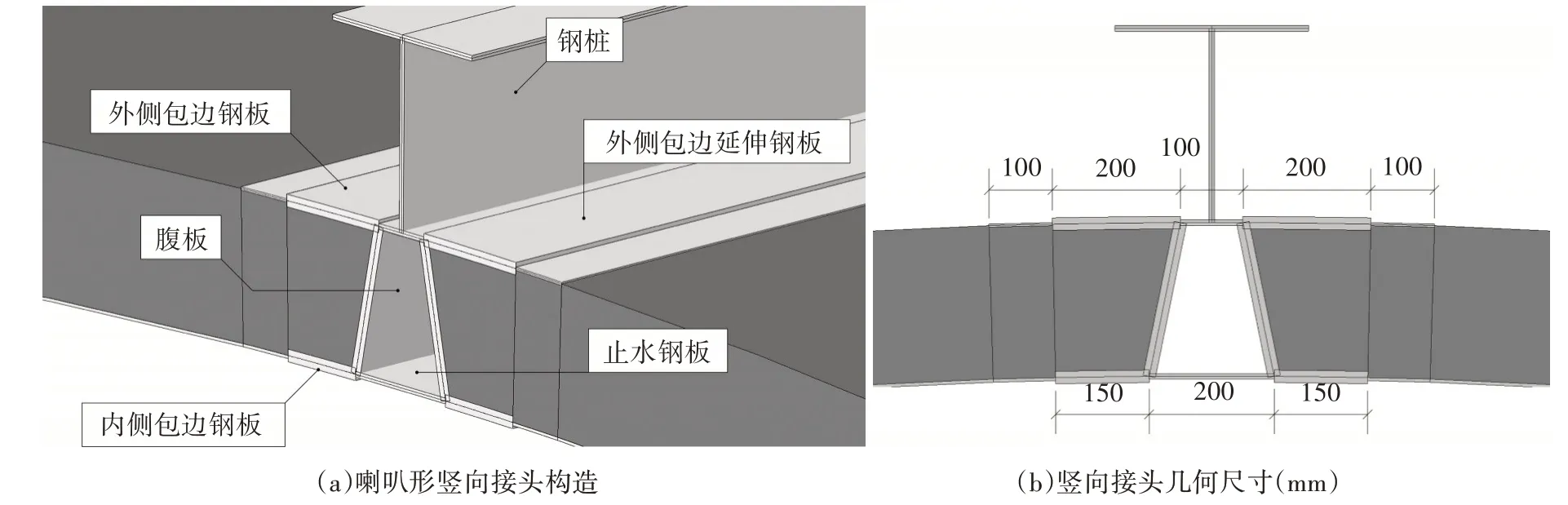
图3 地下装配式大直径组合仓壁喇叭形竖向接头

2.2 组合仓壁稳定性分析

已有的研究［8-9］证明，通过在钢板上设置间距合理的栓钉能保证钢板混凝土组合构件在弹性受力阶段，其钢板与混凝土可协同受力变形，两种材料之间可近似看作是刚性连接。

根据前文设计的仓壁竖向接头形式，建立直径为12.5 m、径厚比100∶1的地下装配式钢板-混凝土仓壁数值模型，模型参数参见表1。仓壁混凝土采用C3D8R 实体单元，内侧钢板与竖向接头钢板选择S4R 壳单元，接头材料属性与仓壁内侧钢板相同。装配式组合仓壁模型网格尺寸控制为0.1 m，其边界条件与加载方式与现浇混凝土仓壁相同。内侧钢板、接头钢板与混凝土之间的刚性连接通过共用节点实现。

对接头抗弯刚度为2.16×107～3.24×107N·m2的装配式钢板-混凝土仓壁进行稳定性分析，屈曲荷载数值解见表3。接头刚度不同的装配式组合仓壁一阶屈曲模态如图4 所示。由图4 可知，模型ACSW-1～ACSW-8 均为“椭圆形”整体屈曲，与文献［10］中均布荷载作用下单层薄壁圆筒一阶屈曲模态一致。

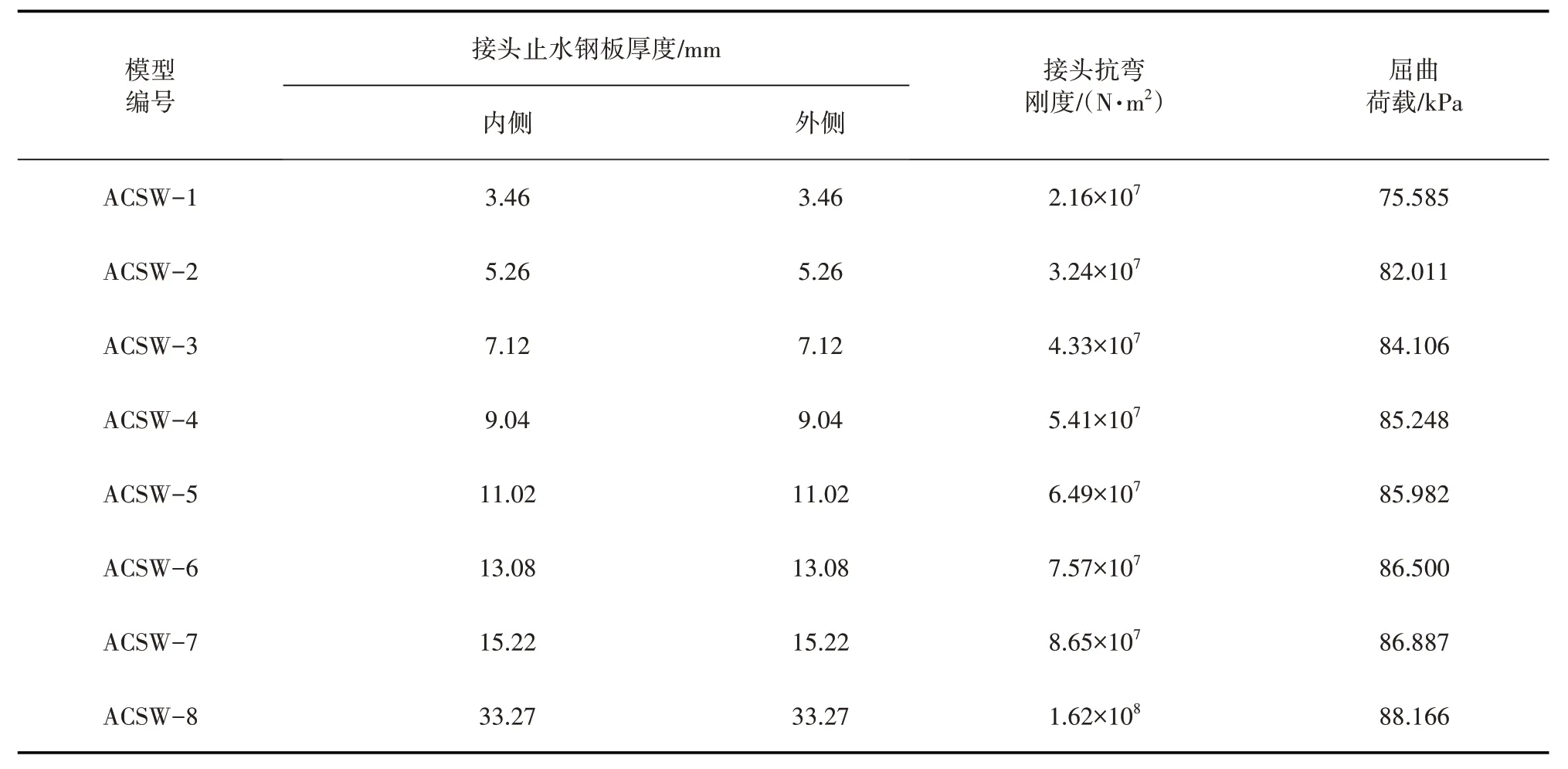
表3 地下装配式钢板-混凝土仓壁屈曲分析数值解

图4 地下装配式钢板-混凝土仓壁一阶屈曲模态

对与装配式钢板-混凝土组合仓壁有相同几何尺寸和材料属性的现浇（无接头）钢板-混凝土仓壁进行稳定性分析，得到的一阶屈曲模态为与图4 相似的“椭圆形”，现浇组合仓壁的屈曲荷载数值解为84.210 kPa。

组合仓壁截面抗弯刚度为D1，竖向接头截面抗弯刚度为D2，现浇组合仓壁屈曲荷载为Pcr1，装配式组合仓壁的屈曲荷载为Pcr2。定义刚度比γ=D2/D1，荷载比λ=Pcr2/Pcr1，得到刚度比-荷载比曲线如图5所示。由图5 可知，随着刚度比γ的增大，荷载比λ逐渐增大但增幅逐渐减小。当γ不小于1 时，装配式钢板-混凝土组合仓壁屈曲荷载与现浇组合仓壁屈曲荷载之比λ不小于1，即此时装配式组合仓壁屈曲荷载不小于现浇组合仓壁，此时喇叭形竖向接头钢板厚度为9.04 mm。

图5 地下装配式钢板-混凝土仓壁刚度比-荷载比关系曲线

对图4 中各点进行拟合，得到荷载比λ与刚度比γ的拟合曲线关系式，见式（2）。

通过式（2）可将装配式组合仓壁屈曲荷载等效为现浇组合仓壁进行整体稳定性验算。首先，根据装配式组合仓壁的内径、仓壁外层混凝土厚度、仓壁内衬钢板厚度和材料参数建立复合圆筒壳有限元数值模型，计算其在均布荷载作用下的屈曲荷载Pcr1；其次，计算装配式组合仓壁竖向接头的抗弯刚度D2和组合仓壁截面抗弯刚度D1，将接头抗弯刚度D2与组合仓壁抗弯刚度D1之比γ代入到式（2）中，计算得到荷载比λ；最后，代入λ=Pcr2/Pcr1，得到装配式组合仓壁在径向均布荷载作用下的极限稳定承载力。

3 结语

本研究对采用喇叭形竖向接头的地下大直径装配式钢板-混凝土筒仓组合仓壁在径向均布荷载作用下的整体稳定性进行分析，得到以下3个结论。

①采用喇叭形竖向接头的钢板-混凝土仓壁的一阶屈曲模态为“椭圆形”整体屈曲，与现浇混凝土仓壁和无接头钢板-混凝土组合仓壁的一阶屈曲模态一致。

②通过改变竖向接头抗弯刚度，得到大直径装配式钢板-混凝土组合仓壁的刚度比-荷载比关系曲线，结果表明：当接头抗弯刚度不小于组合仓壁截面抗弯刚度时，装配式钢板-混凝土仓壁的屈曲荷载不小于现浇钢板-混凝土组合仓壁。

③通过刚度比-荷载比曲线，得到可用于计算地下装配式钢板-混凝土仓壁极限稳定承载力的关系式。