量子近似优化算法在约束优化问题中的应用

刘 畅,张学锋

安徽工业大学 计算机科学与技术学院,安徽 马鞍山 243000

1 引 言

量子近似优化算法(Quantum Approximate Optimization Algorithm,QAOA)是一种可变量子算法,旨在为组合优化问题提供解决方案。由于量子近似优化算法的核心问题是计算目标哈密顿量期望值,在一般的浅层量子电路上,能否找到一种求解量子期望值的有效经典算法以便快速获取最佳可变参数对于在含噪声的中型量子硬件上展示潜在的量子优势至关重要。在量子近似优化算法背景下求解带约束的组合优化问题时,需要找到一种将问题的约束编码到方案中的方法。对于约束问题,在QAOA中有两种处理约束的方法。

第一种是二次无约束二元优化方法,是当有约束违反时,在目标算符中加入惩罚项[1-3],将不符合解的期望值降低,但初始时需要在全部解集上迭代,使得迭代次数变多。另一种方法是量子交替拟设方法,主要思想是重新设计编码了约束条件的演化算符,使得量子态演化限制在可行解范围内[4-6],虽然初始时混合操作被限制在可行解空间中,但向目标函数演化时,最优解的期望值不一定是最优的,使得用该方法求解出问题的最优解不一定是问题的最优解,准确性较低。

对于约束优化问题融合了二次无约束二元优化方法和量子交替拟设方法这两种方法,通过将约束问题中不符合约束条件的解剔除,只留下可行解作为量子近似优化算法框架的初始基态,使得混合操作在初始基态上进行。数值证明了这可以提供更高质量的解。并在目标函数中添加惩罚项,将对角线中不符合解的期望降低。将一个约束问题转变成一个无约束问题,从而高质量解决一般约束问题。

2 最小顶点覆盖问题

最小顶点覆盖(Minimum Vertex Cover,MVC)问题是一个著名的NP-hard问题[7]。最小顶点覆盖问题描述为:给定一个图G=(V,E),其中V是图的顶点集,E是边集。A为V的子集,若G中的每一条边都至少接触集合A中的一个顶点,则称A为覆盖集,包含顶点最少的A则称为最小顶点覆盖集。

A中的顶点可用一个取值为0或1的变量xi表示,xi=1表示图中对应的顶点i在覆盖集A中,xi=0表示顶点i不在A中。那么,A可以用向量x表示,x=(xi)∈{0,1}|V|,并满足约束:任意的(i,j)∈E,xi=1或者xj=1。由此,该问题即是寻找x*:

|x*|=minimize∑i∈Vxi

subject to all(i,j)∈E,thenxi=1∨xj=1

3 量子近似优化算法

3.1 绝热量子计算

绝热量子计算(Adiabatic Quantum Computation,AQC)是一种通过连续绝热量子演化的方式来解决计算问题的量子计算模型。对于一个物理系统,其哈密顿量是可以调控的。针对一个给定的问题,找到目标哈密顿量,在准备一个具有简单哈密顿量的系统并初始化为基态,简单的哈密顿量绝热地演化为期望的目标哈密顿量。最后系统的状态描述了问题的解决方案。

绝热量子计算是通过以下过程解决特定问题和其他组合搜索问题。通常这种问题就是寻找一种状态满足C1∧C2∧…∧CM,表达式包含可满足条件的M个子问题,每个子问题Ci值为True或 False,并且可能包含n位,这里的每一位都是一个变量xj∈{0,1} 所以Ci是一个关于x1,x2,…,xn的布尔值函数,绝热量子算法利用量子绝热演化解决了这类问题。它以初始哈密顿量HB开始:

HB=HB1+HB2+…+HBM

这里HBi对应于该子问题Ci的哈密顿量,通常选择的HBi不会依赖于其他的子问题。然后经历绝热演化,以问题的哈密顿量Hp结束:

这里HP,C是满足问题C的哈密顿量,它有特征值0和1。如果子问题C满足条件,则特征值为1,不满足则特征值为0。对于一个简单的绝热演化路径,如图1所示。

这就是算法的绝热演化哈密顿量。

图1 绝热演化路径Fig.1 Adiabatic evolutionary path

根据绝热定理,从哈密顿量的基态开始HB,首先,经历一个绝热过程,最后以问题哈密顿量的基态结束HP;然后测量最终状态n个自旋的z分量,这将产生一个字符串Z1,Z2,…,Zn这很可能就是问题的结果。

3.2 量子近似优化算法

量子近似优化算法是由Farhi等提出的一种启发式算法,作为一种近似算法,它并不是给出最好的结果,而是给出一个“足够好”的结果。量子近似优化算法是一种利用经典和量子资源寻找组合优化问题近似解的算法框架[8-10],从量子绝热算法的近似推导而来。在求解具有约束的组合优化问题时,需要找到一种将问题约束编码到方案中的方法,并通过期望的质量来解决每个问题实例。

图2 QAOA的工作流程Fig.2 Work flow of quantum approximate optimization algorithm(QAOA)

(1)

(2)

3.3 二次无约束二元优化方法

二次无约束二元优化方法是对量子近似优化算法的改进算法,现已被广泛研究,并被用于建模和解决许多类别的优化问题。约束优化问题的目标是最小化或最大化一个代价函数,这个代价函数在物理上可以解释为找到一个典型的伊辛哈密顿函数的基态。二次无约束二元优化方法通过预处理将问题的约束条件转换到代价函数中,从而提高解的质量和运行时间。二次无约束二元优化的一个主要优点是它提供了一个统一的算法框架,适用于解决许多类型的问题。

3.4 量子交替拟设方法

HADFIELD等扩展了量子近似优化算法框架,根据不同问题设置了不同的基态代替了固定的初始基态,将全集均匀叠加态转化为可行解均匀叠加态,这个扩展的实质被称为量子交替算符拟设方法。对于只需要在期望的子空间内进行混合的情况,初始哈密顿量在可行解子空间基态上混合运行能够得到比在原始框架中更高效的结果。这种方法对于具有约束的优化问题特别有用,将满足约束条件的集合定义为一个可行解子空间。使得在量子近似优化算法的框架下更高效地得到问题的最好结果。

4 基于QAOA的MVC问题求解

4.1 提出方法的算法描述

根据最小顶点覆盖问题的定义,给出了在量子近似优化算法框架中的解决方案。求解的过程如算法1所示:

算法1: 求解最小顶点覆盖问题输入:图G=(V,E),迭代次数p输出:最小顶点覆盖集A1) A←satisfy_constraints(G) //satisfy_constraints为求解出图G的满足约束的所有解,A为可行解集合2) Ω←x∈binary_systemA(){} //binary_system为将集合A转化为二进制集合,x为二进制向量3) 初始化:β→,γ→←rand-π,π()4) |s〉←Ω5) B^←∑ni=1σ(xiσxi+1+σyiσyi+1)6) C^←∑2n-1x=0x→·e→|x〉〈x|+2∗∑i,j()∈Eσzi+12∗σzj+127) ψβ→,γ→()〉←e-iβpB^e-iγpC^…e-iβ1B^e-iγ1C^s〉8) fβ→,γ→()←〈ψβ→,γ→()C^ψβ→,γ→()〉9) β∗,γ∗←Simplex_optimize(argmaxβ→ ,γ→f(β→,γ→)) //Simplex_optimize为单纯性优化方法10) A←measure_max(|ψβ→,γ→()〉 //测量ψβ→,γ→()中最大概率对应的二进制向量A11) return A

(3)

(4)

4.2 对比方法的算法描述

在本节中,将讨论一些对比方法。

(3) 热启动量子近似优化算法。Egger等[14]对经典算法做了两个主要的修改。首先,初始的叠加态如式(5)所示:

(5)

(6)

连续松弛解c*可以等于0或1,但最优离散解可以分别为1或0。在实验中,将设置为0.25(与原作者一致)。

4.3 实验结果与讨论

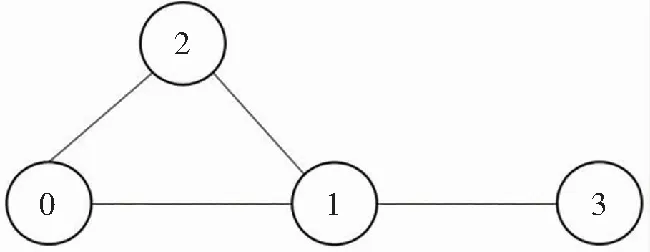
(a) 一个最小顶点覆盖问题实例

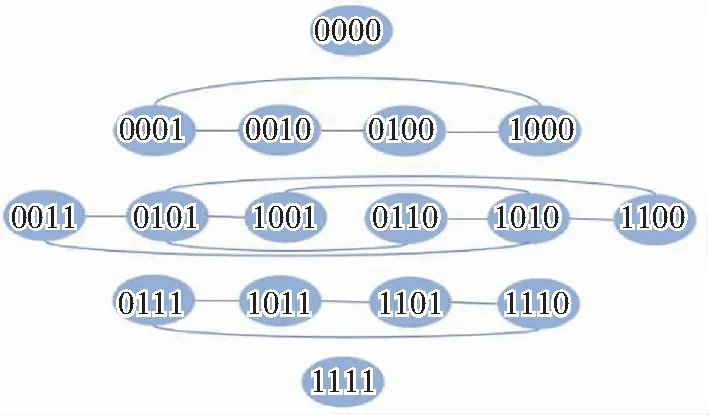
(b) 提出方法的连接结构

(c) 提出方法运行得到的期望值图3 提出方法在实例运行下的结果Fig.3 The results of the proposed method running in an example

图4给出了在10个随机图上运行各种方法得到的近似比。从图4可以看出,随着p的增加,所有方案平均解的质量都有所提高。提出的方法优于经典方法,QAOA+,热启动量子近似优化算法,提出的方法在p=3时,就已经趋于最高近似比。

图4 随演化步数增大时的近似比Fig.4 The approximate ratio as the number of evolutionary steps increases

图4中QAOA+算法的性能相比其他3种方法得到的近似比收敛效果最差。因为Farhi等提出QAOA+,这是为了为通过解析的方式分析每一步的效果,并不是为了提高算法的性能。经典方法优于热启动量子近似优化算法,热启动量子近似优化算法是将离散的初始解变为连续的初始解状态,一个好的松弛初始解可以缩短到最优解的进化距离。但实验结果可以看出,使用连续解得到的最终最优解与问题最优解相差甚远。反之,无偏差的均匀叠加状态更有利于后续进化到最终最优状态。

提出的方法优于经典方法,因为提出的方法的演化空间更小,收敛到最优解的迭代次数减少。所以在图4中,可以看到提出的算法的性能非常优异。

5 结 论

研究提出了新的方法并回顾了现有的方法,将这些方法应用到带有约束的最小顶点覆盖问题中。提出的方法中,先确定可行解空间,使初始态为可行解的均匀叠加态。这样做缩小了初始态的范围,使混合操作限定在可行解空间内, 对混合算子进行了约束,将一个不等式约束问题转化为等式约束问题。再在目标函数中添加惩罚项,将对角线中不符合解的期望降低。将一个约束问题转变成一个无约束问题。同其他方法相比较,方案可高效率、高准确性地解决问题。

在未来的工作中,计划将提出的方案变成量子线路。并将应用于其他约束组合优化问题,如最大割问题、旅行商问题等。这些问题在许多学科中都有重要的应用,并将研究基于机器学习的量子近似优化算法方法应用于约束组合优化问题中。