混合策略改进型秃鹰搜索算法

曹 慧,秦江涛

上海理工大学 管理学院,上海 200093

1 引 言

随着科学技术的进步,需要解决的优化问题越来越多,如函数极值、聚类问题等,大多都具有复杂、多维、非线性等特点,用常规的数学方法难以解决。因此一些学者根据大自然中种群活动或自然规律的启发提出多种元启发式优化算法[1],这类算法通过模拟生物行为或物理现象,建立不同的数学模型以解决优化问题。常见的元启发式算法有粒子群优化算法(PSO)[2],遗传算法(GA)[3],灰狼优化算法(GWO)[4],鲸鱼优化算法(WOA)[5],蚁狮优化算法(ALO)[6],麻雀搜索算法(SSA)[7]等。这些元启发式算法具备方法简便,参数少,易于实现等优势,可以解决不同类型的优化问题,目前多被用于特征选择、路径规划等相关领域[8-12]。此外,一些学者对这类算法也进行了相应的改进,以进一步增强算法的性能。但按照NFL(No Free Lunch)[13]理论,不存在一种可以独立处理全部优化问题的元启发式算法,因此应不断探索新算法并对算法进行改进。

秃鹰搜索算法(Bald Eagle Search,BES)在2020年由Alsattar等[14]受秃鹰的搜索和狩猎行为的启发而提出的元启发式算法。目前,国内外一些学者已将秃鹰搜索算法应用于实际工程问题的优化,如文献[15]将BES用于支持向量机(SVM),构建了BES-SVM预测模型,BES算法可以对SVM算法进行有效的优化,提高了SVM的预测精度。文献[16]将其应用于光伏参数估计,结果证明所使用的BES算法能够获得更好的光伏参数结果,但学者忽略了BES算法本身所存在的易陷入局部最优等问题。文献[17]将其用来解决水下无线传感器网络(UWSN)的高能耗等问题,根据实验结果,BES算法在UWSN中表现的性能具有极大的优越性。大部分文献将BES算法用于实际问题的优化中,并取得了较好的结果,但是并未考虑BES算法本身所存在的问题。而BES作为新型元启发式算法,类似于其他传统算法,具有收敛速度慢,寻优精度不高等问题,因此文献[18]提出了基于莱维飞行和模拟退火策略的秃鹰搜索算法(IBES),使用莱维飞行扩大群体的搜索范围,模拟退火策略增强原算法在局部邻域内求解精度,算法的性能得到一定程度的改善,但该算法侧重于跳出局部最优解,收敛速度和精度还有一定的提高空间。

上述改进策略侧重于算法跳出局部最优,在提升算法局部搜索上具有一定的改善,但是对于算法的收敛速度以及平衡局部和全局搜索方面还具有很大的改进空间。为了弥补这些不足,本文将提出一种混合策略改进型秃鹰搜索算法(HSIBES),此算法利用Logistic映射策略初始化种群,使其分布更加均匀,有助于算法在全局范围内搜索。考虑莱维飞行具有长短步长交替搜索的特点,使用莱维飞行进行搜索空间中步长的控制,扩大搜寻区域,提高算法跳出局部极值点的能力。最后使用自适应惯性权重,协调秃鹰搜索算法在局部以及全局范围内的寻优能力,提高算法寻优的精度和速度。将HSIBES算法在9个基准测试函数上进行仿真实验,并且进行Wilcoxon秩和检验。实验结果说明本文提出的HSIBES算法具有更快的收敛速度和更高的收敛精度,可以更好地平衡全局和局部搜索能力。

2 秃鹰搜索算法

秃鹰种群主要分布于北美地区, 它们具有视力敏锐,观察能力优秀的特点。在进行捕食食物时,秃鹰种群会先根据食物的浓度来确定搜寻空间,之后飞向所确定的区域;接着在所选择的搜寻空间中搜寻食物;最终秃鹰根据食物所在的位置,慢慢改变飞行高度,加速向下飞行,直至成功获取猎物。

Alsattar 等根据秃鹰捕获食物的活动建立了秃鹰搜索算法(BES)数学模型,算法可以总结为3个阶段,分别是选取搜寻空间、搜寻空间食物以及俯冲捕获食物。

2.1 选取搜寻空间

秃鹰选取搜寻区域,根据区域内食物的数量选择最优搜索位置,易于搜寻食物,该行为用数学模型表示如下:

Pi,new=Pbest+α×r×(Pmean-Pi)

(1)

式(1)中:α是控制秃鹰位置改变的因子,取值在1.5和2之间;r是0和1之间的随机数;Pi,new为秃鹰的更新位置;Pbest是秃鹰种群搜寻选择的最优位置;Pmean是当前种群的平均位置;Pi表示种群中第i只个体的位置。

2.2 搜寻空间食物(探索)

在此搜索阶段,秃鹰种群在确定的搜寻空间中搜寻食物,并在空间中以螺旋状飞行,加速对猎物的追捕,寻求最优向下飞行捕获食物的位置。秃鹰种群以螺旋状搜寻食物的飞行轨迹可用以下数学模型进行表示:

θ(i)=a×π×rand()

(2)

r(i)=θ(i)+R×rand()

(3)

xr(i)=r(i)×sin(θ(i))

(4)

yr(i)=r(i)×cos(θ(i))

(5)

x(i)=xr(i)/max(|xr|)

(6)

y(i)=yr(i)/max(|yr|)

(7)

其中:θ(i)表示螺旋方程的极角,r(i)表示螺旋方程的极径;a表示控制螺旋轨迹的因子介于5至10之间,R用来确定搜索周期数,取值在0.5至2之间,x(i)与y(i)为极坐标方程中个体所处的位置,取值范围均在-1到1之间。秃鹰位置更新如下:

Pi,new=Pi+x(i)×(Pi-Pmean)+y(i)×(Pi-Pi+1)

(8)

2.3 俯冲捕获猎物

秃鹰从所选择的搜寻区域的最优位置加速飞向目标食物,所有个体也会飞向最优位置去捕获食物,飞行轨迹仍然使用极坐标数学模型进行描述,公式如下:

θ(i)=a×π×rand()

(9)

r(i)=θ(i)

(10)

xr(i)=r(i)×sinh(θ(i))

(11)

yr(i)=r(i)×cosh(θ(i))

(12)

x1(i)=xr(i)/max(|xr|)

(13)

y1(i)=yr(i)/max(|yr|)

(14)

加速飞向目标过程中秃鹰的位置更新公式为

(15)

Pi,new=rand×Pbest+δx+δy

(16)

其中:c1和c2分别表示秃鹰向最佳位置与中心位置的运动强度,取值区间均为[1,2]。

3 混合策略改进型秃鹰搜索算法

标准的秃鹰搜索算法与其他标准元启发算法相比有良好的收敛速度和收敛精度,但与其余基准元启发式算法相同也存在寻优精度低,易陷入局部最优的缺陷,为了提升收敛速度和精度,提出了一种混合策略改进型秃鹰搜索算法,并设计了3种改进策略,分别是:Logistic混沌映射,进行种群初始化,增加种群多样性;莱维飞行,控制步长,扩大搜索范围,跳出局部最优解;自适应惯性权重,改善群体之间的信息交流,平衡局部和全局搜索能力。

3.1 Logistic混沌映射

秃鹰搜索算法采用随机法初始化种群,使得秃鹰个体在搜索空间内分布不均匀,从而导致算法在解空间的遍历性低,降低收敛速度和求解精度。将Logistic混沌映射[19]引入BES算法,增加种群的多样性,提高算法的收敛速度并提升算法在全局范围内的寻优能力,其数学模型如下所示:

yt+1=μyt(1-yt)

(17)

式(17)中,yt表示第t次迭代产生的混沌变量,取值范围为[0,1],μ为控制参数,取值范围为[0,4]。当μ的取值为4时,变量会遍历整个搜索空间。

将获得的混沌序列yt通过下式逆映射到搜寻空间中,得到初始化种群Pt:

Pt=Lt+(Ut-Lt)yt

(18)

其中,Ut和Lt分别为搜索空间的上界和下界。

3.2 莱维飞行

莱维飞行[20]是一个随机漫步的过程,由法国数学家莱维提出,莱维飞行大步长与小步长随机交替,可有效跳出局部最优。由于秃鹰搜索算法在选择搜索空间阶段的搜索步长是一个定值,容易陷入局部最优。而引入莱维飞行能够控制步长,扩大搜索范围,使算法有机会跳出局部最优解。根据莱维飞行,改进后的选择搜索空间阶段位置更新函数如下:

Pi,new=Pbest+α*r(Pmean-Pi)×Levy

(19)

Levy符合莱维分布,满足Levy(λ)～u=t-λ(1<λ≤3)。由于莱维飞行的复杂性,通常使用Mantegna算法对其进行模拟[21],步长S的计算式为

(20)

式(20)中,u、v均遵循正态分布:

(21)

(22)

其中,τ为Gamma函数,参数β=1.5。

3.3 自适应惯性权重

在搜寻空间食物中只依照当前秃鹰种群的信息来更新所处位置,而未考虑其余迭代中出现的位置信息,会导致在搜索更新位置中,位置更新不准确,并在一定程度上限制了算法的搜索效率。因此,将引入自适应惯性权重,在权重值较大的情况下,算法的在全局范围内的搜寻能力比较强,在权值较小的情况下,算法后期在局部范围内的寻优能力较强。因此,加入自适应惯性权重,可以有效改善群体之间的信息交流,平衡局部和全局搜索能力,提高算法寻优的精度和速度[22]。

自适应权重公式如式(23)所示:

ω=sin((π×p)/(2×M)+π)+1

(23)

其中,p为当前迭代次数,M为最大迭代次数。

将式(23)代入式(8),得到改进的秃鹰位置更新函数:

Pi,new=Pi+ω×x(i)×(Pi-Pmean)+ω×y(i)×(Pi-Pi+1)

(24)

3.4 算法流程

step1：初始化秃鹰算法种群规模,空间维度等参数,使用Logistic混沌映射进行秃鹰种群初始化;

step2：计算适应度值,获得最优个体;

step3：秃鹰选择搜索空间,利用式(19)更新位置;

step4：秃鹰在搜索空间搜索猎物,利用式(24)更新位置;

step5：秃鹰俯冲利用式(16),更新位置;

step6：当符合结束条件时,输出最优结果,否则继续进行从step2到step6的流程。

3.5 时间复杂度分析

假设种群规模为N,空间维度为D,则BES算法参数初始化的时间复杂度为O(1),计算函数适应度为O(N),迭代过程中种群复杂为O(ND),BES算法总的时间复杂度为

O(1)+O(N)+O(ND)=O(ND)

(25)

在HSIBES算法中,随机初始化替换为Logistic混沌初始化时间复杂度为O(ND),计算适应度为O(N),引入莱维飞行和自适应惯性权重进行位置更新所对应的时间复杂度均为O(ND),则HSIBES算法总的时间复杂度为

O(ND)+O(N)+O(ND)+O(ND)=O(ND)

(26)

基于上述分析,HSIBES算法和BES算法相比,时间复杂度并未增加。

4 实验结果分析

实验测试结果均在Intel(R) Core(TM) i7-10750H CPU @ 2.60GHz,64位Windows10操作系统和MATLAB R2018b上实现。

为了验证混合策略改进型秃鹰搜索算法的有效性,将从以下几个部分进行实验验证:

(1) 将HSIBES与基本秃鹰搜索算法(BES)[14]、粒子群优化算法(PSO)[2]、鲸鱼优化算法(WOA)[5]、蚁狮算法(ALO)[6]、灰狼优化算法(GWO)[4]这5个基本元启发式算法进行对比,验证混合策略改进型秃鹰搜索算法的寻优能力和鲁棒性。

(2) 将HSIBES与文献[18]中改进的秃鹰搜索算法进行对比,验证本文改进算法具有一定的竞争力。

(3) 通过Wilcoxon秩和检验进行差异性检验,验证HSIBES算法与其他对比算法的差异性。

为了检验提出的改进的秃鹰搜索算法的鲁棒性以及有效性,从文献[23]中选择了9个具备不同特征的基准测试函数进行实验测试,具体函数表达式如表1所示。这9个用于实验的测试函数主要分为单峰函数以及多峰函数,其中f1(x)—f6(x)是单峰函数,f7(x)—f9(x)是多峰函数,算法的局部搜索能力与收敛速度可用f1(x)-f6(x)测试,算法在全局范围内的寻优能力以及跳出局部极值点的能力可用f7(x)—f9(x)测试。

表1 基本测试函数Table 1 Basic test functions

4.1 与其他基准算法进行对比

将提出的HSIBES算法与BES[14]、PSO[2]、WOA[5]、ALO[6]、GWO[4]算法在9个基准测试函数上进行对比实验,为保证实验的公平性,种群规模均设为30,最大迭代次数为500,维度设为30维,各个算法其他参数设置与相应参考文献一致,实验将记录每种算法在测试函数上独立运行30次的平均值、方差和平均耗时以便进行对比,结果如表2所示。

表2 函数测试实验结果Table 2 Results of function test experiment

从均值来看,提出的HSIBES算法在测试函数f7(x)和f9(x)的均值达到了理论最优值,说明30次独立运行中得到的结果精度较高,稳定性较好。HSIBES算法在测试函数f5(x)的均值结果不是算法结果里最优的,劣于其他算法,但是差异不是非常显著,求解精度在1个数量级以内,在可以接受的范围内。在测试函数f1(x)—f4(x),f6(x),f8(x)上HSIBES算法明显优于其他对比算法,尤其在函数f1(x)、f3(x)和f4(x)上,HSIBES算法相较于BES、GWO、ALO、PSO、WOA均提升了100～200个数量级左右。在f2(x)、f6(x)和f8(x)函数上也提升了多个数量级,说明混合策略改进型秃鹰搜索算法求解精度较好。从标准差来看HSIBES算法测试函数上的标准差均是所有结果里最优的,说明提出的算法的鲁棒性较好。从平均耗时来看,PSO算法整体耗时最短,HSIBES算法相对于标准BES的平均耗时要小,说明引进的改进策略并未降低原算法的执行效率。经过上述分析,HSIBES算法在平均值标准差以及耗时方面整体来说要优于对比算法,具有较好的收敛速度和收敛精度,稳定性也较好。

4.2 与其他改进算法的对比

为了突出提出的混合策略改进型秃鹰搜索算法相比于其他学者改进的秃鹰搜索算法的竞争优势,选取文献[18]改进的秃鹰搜索算法IBES进行对比,和上文设置统一的参数条件:c1=c2=α=2,a=10,R=1.5,种群规模均设为30,最大迭代次数为500,维度设为30维,在上文的测试函数及运行环境上进行测试,独立运行30次,对所得结果求平均值与标准差,与本文提出的HSIBES进行对比分析,结果如表3所示。

对于函数f1(x)和f3(x),HSIBES算法的平均寻优精度高于IBES算法,高出20个数量级左右,两者的标准差相同,说明两种算法在函数f1(x)和f3(x)的稳定性相当,在测试函数f2(x)、f4(x)和f6(x)上,HSIBES算法的均值和标准差均高于IBES算法,在测试函数f5(x)上,HSIBES算法的寻优精度和稳定性不及IBES,在函数f7(x)—f9(x)上,二者的均值和标准差的求解结果相同。从平均值和标准差来看,HSIBES算法在55%以上的测试函数上优于IBES算法,33%测试函数和IBES算法结果相同。从平均耗时的结果来看,HSIBES算法在9个函数上的耗时都比IBES算法的耗时短。综上,和对比算法IBES相比,HSIBES算法具有一定的竞争优势。

4.3 算法收敛曲线对比分析

为了更加直观地反映HSIBES算法的性能,给出了算法在函数上运行30次中其中一次的收敛图,如图1所示。和其他基本算法相比,HSIBES算法在单峰函数f1(x)—f4(x),f6(x)的收敛速度和收敛精度明显高于其他对比算法,虽然在f5(x)函数上的精度略低于其他算法,但是其收敛速度明显优于其他对比算法,在多峰函数f7(x)—f9(x)上,HSIBES算法可以快速地收敛并且跳出局部最优,说明混合策略改进型秃鹰搜索算法HSIBES可以提高基本算法的收敛速度,跳出局部极值点,进行全局范围的寻优。

和IBES对比算法相比,HSIBES算法除了在函数f5(x)上表现不佳,在其他函数上都有较好的寻优精度和收敛速度。在函数f1(x)—f4(x)上,HSIBES算法和IBES算法相比精度显著提升,在函数f6(x)上HSIBES算法出现了多次拐点,但停滞次数相对较少,并且在后期跳出局部最优解,在函数f7(x)—f9(x)上,HSIBES算法可在较短的时间内和其他改进算法达到相同的寻优值,综上所述本文提出的HSIBES算法具有较好的收敛速度和寻优精度,能更好地平衡算法局部和全局搜索能力。

(a) f1(x)收敛曲线

(b) f2(x)收敛曲线

(c) f3(x)收敛曲线

(d) f4(x)收敛曲线

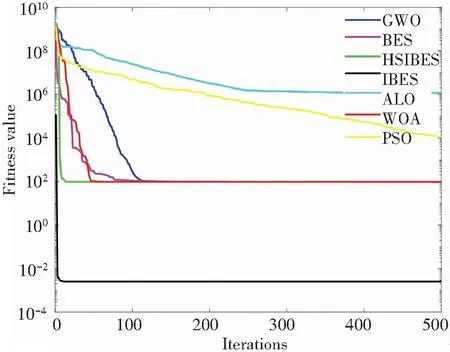
(e) f5(x)收敛曲线

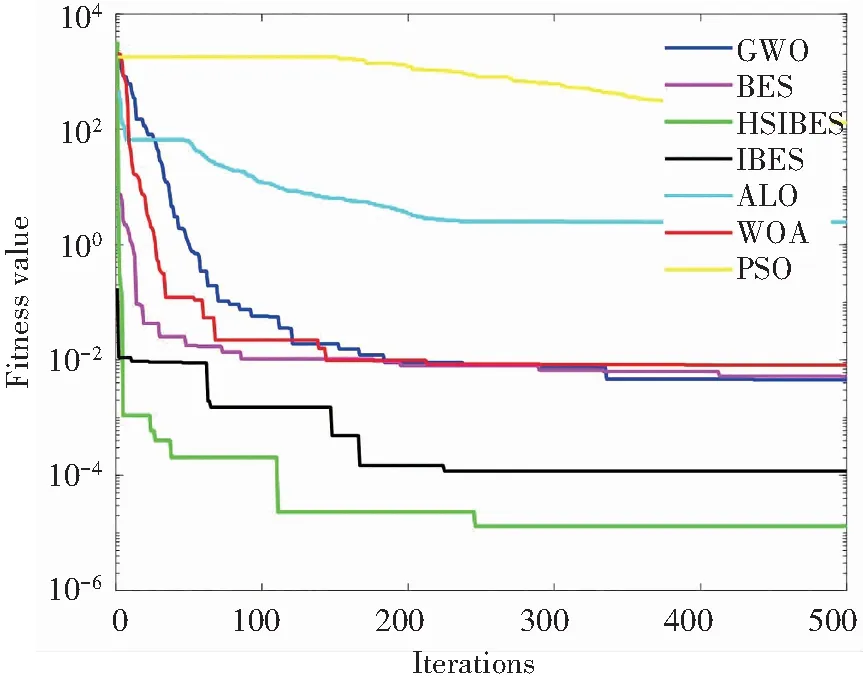
(f) f6(x)收敛曲线

(g) f7(x)收敛曲线

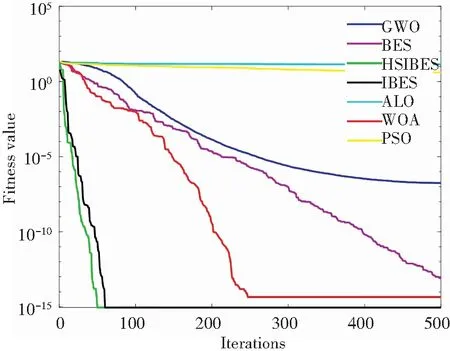
(h) f8(x)收敛曲线

(i) f9(x)收敛曲线图1 各测试函数下的收敛曲线Fig.1 Convergence curves under each test function

4.4 Wilcoxon秩和检验

运用Wilcoxon秩和检验[24]的方法来检验提出的HSIBES算法与其他算法的显著性差别。将获得的实验结果在5%的显著性水平下进行统计检验,在p大于0.05的情况下,说明两种算法性能相差不大,否则两种比较算法的性能具有显著性差异。为了判断HSIBES算法与其他算法的显著性区别,将以上算法在函数上独立运行30次的结果作为样本,进行实验验证。得到的Wilcoxon秩和检验的p值结果如表4所示,由于HSIBES算法不能和本身进行比较,所以在这里不再列出HSIBES算法的p值,当实验样本数据一样时,说明两个对比算法性能相当,此时数据无效,在下表中使用NaN表示。

表4 Wilcoxon秩和检验p值Table 4 Wilcoxon rank and test p-value

由表4可知,根据对比算法在测试函数f7(x)—f9(x)的检验结果来看,HSIBES算法与IBES算法性能相当,在函数f4(x)上,二者性能显著性差异不明显,在函数f7(x)上,HSIBES算法与WOA算法显著性差异不明显,除此之外,其余p值均小于5%,说明HSIBES算法和其他对比算法之间具有显著性差异,总体看来,本文提出的HSIBES算法的优越性在统计上是显著的,与其他对比算法具有显著性差异。

5 结束语

根据BES算法存在易陷入局部最优,收敛精度低的问题,提出了混合策略改进的秃鹰搜索算法(HSIBES),利用Logistic映射策略初始化种群,使种群分布更加均匀,其次引入莱维飞行,其长短步长交替搜索,控制搜索步长,有利于提高解的质量。最后在探索阶段使用自适应惯性权重,提高了算法寻优的精度和速度,平衡了局部和全局探索能力。最后在9个基准测试函数上进行了仿真实验,并与BES、PSO、WOA、ALO、GWO以及其他学者改进的IBES算法进行对比实验,分析得出了提出的HSIBES算法收敛速度、收敛精度以及鲁棒性都表现较好,并通过Wilcoxon秩和检验验证了HSIBES算法与其他算法的显著性差异。在后续的研究中,将会把HSIBES算法用于实际工程问题中,如神经网络的优化,图像分割等。