响应变量随机缺失的相依函数型单指标模型的k近邻估计
何文然,黄振生
南京理工大学 数学与统计学院,南京 210094
1 引 言
过去几十年来,高维数据处理一般采用单指标模型进行降维,一方面可以避免维数灾难问题,另一方面能够保持多元回归中非参数方法的优势。该模型在生物医学、自然科学和经济金融诸多领域已体现出巨大的研究价值和广泛的实际应用前景。伴随着函数型数据分析的热潮,统计学者考虑将单指标模型降维的半参数优点和函数型数据结合,引入了函数型单指标回归模型[1]:
Y=r(〈θ,X〉)+ε
(1)
其中,函数r(·)是未知连接函数,r:R→R;θ是未知函数型单指标参数,取值于可分的Hilbert空间H;ε是随机误差项,满足E(ε|X)=0;Y是标量响应变量;X是函数型协变量,取值于可分的Hilbert空间H。
Ferraty等[1]首先研究函数型单指标模型式(1),给出模型的核估计,并讨论了估计量的渐进性质,但并没有给出单指标函数的估计;随后,Ait-Saïdi等[2]提出采用交叉验证方法估计未知的单指标参数,基于固定带宽,采用核估计得到未知的连接函数,并给出了估计量的渐近一致收敛速度;Attaoui等[3]利用核方法研究函数型单指标模型的条件密度估计,给出估计量的逐点和一致几乎完全收敛速度,特别地,他们利用拟极大似然估计研究了单指标参数;Ferraty等[4]基于泛函导数估计提出一种新的估计方法;Said等[5]在强混合时间序列情况下,得到基于固定带宽的条件密度核估计量在一般条件下的均匀几乎完全收敛速度和渐近正态性,同时给出了估计量的置信区间;此外,Ding等[6]研究一类函数型部分线性单指标模型并提出一种结合局部常数平滑的剖面最小二乘法来估计斜率函数和连接函数。近年来,Novo等[7]第一次在独立条件下,在函数型半参数模型采用k近邻来估计未知连接函数,并讨论单指标已知与未知时估计量的渐近一致收敛速度,同时采用交叉验证来估计未知的单指标参数。但是,他们是在独立样本的条件下研究的,没有考虑相依情况下的函数型数据。
上述所有涉及的贡献都是在完全观测样本下发生的。然而,许多实际工作中,如市场调查、医学研究、信度检验等,一些观察结果可能不完整,通常被称为缺失数据,其统计分析因为内容很少或者缺失,变得非常困难和具有挑战性。随机缺失是最基本的,也是应用最广泛的关于缺失机理的假设。在解释变量为有限维时,可以在统计文献中找到许多这种情况的例子及其回归模型的统计推断。当解释变量为无限的情况或有函数型特征时,有很少的文献研究缺失数据的模型,仅有Ferraty等[8]基于独立同分布样本研究了响应变量随机缺失的函数型非参数回归模型;Ling等[9]同样基于函数型非参数模型,利用函数型平稳遍历数据研究了未知估计量的渐近性质。近年来,Febrero-Bande等[10]基于函数型线性回归模型,对于独立同分布样本下的标量响应随机缺失的函数型数据,提出一种效率更高的新模型估计方法;Ling等[11]则对于响应变量随机缺失的强混合时间序列数据,研究了函数型单指数回归模型的未知参数和未知函数的估计,同时在一些正则条件下,得到了估计量的一致几乎完全收敛速度以及渐近正态性。
综上所述,函数型数据分析方法大多是在独立同分布的情形下研究的,与之相比,具有强混合时间序列的数据分析并没有受到广大学者的足够重视。函数型单指标模型作为一种半参数模型,同时具有参数模型和非参模型的优势,通常的估计方法一般为经典核方法,具有更强数据适用性的k近邻方法并没有被普及,且同时对于响应变量随机缺失的情形,参考文献至今未被研究。但是响应变量随机缺失的缺失数据,以及具有强混合结构的函数型时间序列数据是一类重要的亟待处理的问题。
受以上论文的启发,本文在强混合函数型时间序列数据和响应变量随机缺失下研究模型式(1)。利用具有局部窗宽的k近邻方法估计给出未知连接函数的估计量,改进了具有全局窗宽的函数型经典核方法。k近邻方法可以自适应调整窗宽,对数据具有更好的适用性,利用模拟研究对比k近邻方法和函数型经典核方法的估计精度,验证所提模型和方法的有效性。同时,用两种估计方法对同一个实际例子进行分析拟合,通过实际数据拟合的好坏进一步说明k近邻估计方法的优越性。
文章的剩余部分如下:第一章给出了模型的估计方法,第二章进行了数值模拟,第三章给进行了实例分析,在第四章给出了结论。
2 函数型单指标模型和估计

考虑以下函数型单指标模型:
Y=r(〈Xi,θ〉)+εi,i=1,2,…,n
(2)
假设{(Xi,δi,Yi),1≤i≤n} 是一列来自总体 (X,δ,Y) 的函数型数据样本,Yi∈R;Xi∈H;θ∈θ(t),取值于可分的 Hilbert 空间H,t∈R;d(·,·) 为空间H上的半度量,dθ(x1,x2)=|〈x1-x2,θ〉|;εi要满足E(εi|Xi)=0;同时当Yi缺失时,δi=0, 否则δi=1; 假设P(δi=1|Yi,xi)=P(δi=1|xi)=p(xi),i=1,2,…,n。
类似于Ling等[11],r(〈θ,x〉) 的k近邻估计量构造如下:
其中,
上式中包含的K(·) 为核函数, 而Hn,k,θ(x) 为随机窗宽,定义如下:
其中,Bθ(x,h) 为以x为中心,h(h>0) 为半径的小球 ,IBθ(x,h)(·) 为集合的示性函数。若Hn,k,θ(x)=hn(x), 其中hn(x) 为一列非负随机正序列, 且随着n→∞,hn(x)→0,则类似于Kudrasz等[11]提出的经典核估计, 窗宽依赖于固定点, 表达式如下:
实际操作中,函数型单指标θ无法通过先验知识知晓, 为此需要一个估计它的方法。 这里和Ling等[11]一致, 借用Ding等[7]的一个想法, 采用剖面最小二乘法结合局部平滑常数技术来估计θ。
下面给出估计流程。
步骤1 构建含参数(θ)的目标损失函数:
步骤2 基于剖面最小二乘法,结合局部平滑常数技术来估计θ。将θ分解为协方差函数主成分分解得到的基函数的累加和形式,同时确定主成分基函数的数目,最后将估计函数的问题变为估计基函数前系数的问题。
步骤3 步骤1的含参(θ)目标函数,变为了未知量的基函数前系数,对损失函数求解最小值得到系数。

3 数值模拟
本节的目的是通过模拟对比k近邻方法(kNN)与经典核方法(NW), 以验证本文所提方法的有效性。基于模型式(2), 函数型解释变量Xi=Xi(t)由以下函数生成:


图1 曲线xi=1,…,200(tj),tj=1,…,100∈[0,π/3]Fig.1 Curve xi=1,…,200(tj),tj=1,…,100∈[0,π/3]
函数型单指标参数构造如下:
本文的θ(t) 估计方法同Ling 等[11]一致,用积分平方误差FRISE作为评价指标来评价θ(t)估计的好坏。


本文的缺失机制,参考Ling等[11],缺失机制满足:
其中,p(x)=P(δ=1|X=x),对任意w∈R,有exgit(w)=ew/(1+ew)。这里参数α控制缺失率,当α增加时,缺失率下降,这里选取α=2。
如表1所示,模拟研究了单指标θ已知、未知情形下,k近邻方法与经典核方法预测效果的好坏,评价指标为平均均方误差;同时也考虑k近邻方法与经典核方法对未知参数θ的估计优劣。模拟时,将样本分为训练集与预测集,用训练集来训练带宽,其中经典核方法为全局最优带宽,k近邻方法为自适应窗宽,它可以基于样本得到一个个局部窗宽,对样本的适应性更优。为了方便,预测集样本量统一设置为100。表1中的n为训练集样本量,同时对每个样本重复200次。

表1 两种方法在不同样本量下的积分平方误差和 平均均方误差Table 1 The integral square error and mean square error of the two methods under different sample sizes
从表1可以看出:在单指标θ未知情况下,预测集中,k近邻方法的估计精度要优于经典核方法。在训练样本量为100时,相比于经典核方法,k近邻方法对应的平均均方误差下降了47%,在训练样本量为300时,下降了60%。这说明随着样本量增加,k近邻方法比经典核方法估计效果更优。
在单指标θ已知情况下,同样在预测集中,k近邻方法的估计精度也要优于经典核方法,同样地,随着样本量的增加,k近邻方法的改进幅度要大于经典核方法。在训练样本量为100时,相比于经典核方法,k近邻方法对应的平均均方误差下降了45%,在训练样本量为300时,下降了60%,且相比于θ未知的时候,k近邻方法与经典核方法估计精度都得到了提高。因此,对θ估计效果的好坏也是影响最终估计效果的一个重要因素。
从表1可以看出:在估计θ时,k近邻方法的表现也要优于经典核方法,同时随着样本量的增大,k近邻方法对θ估计效果的提升也要高于经典核方法。在训练样本量为100时,相比经典核方法,k近邻对应的平均均方误差下降了37%,在训练样本量为300时,下降了39%。
在训练集中,k近邻方法的表现也同样优于经典核方法。
在训练集中,当θ未知时,可以看到k近邻方法的估计精度要优于经典核方法。随着样本量的增加,k近邻方法的改进幅度要大于经典核方法。在训练样本量为100时,相比于经典核方法,k近邻方法对应的平均均方误差下降了46%,在训练样本量为300时,下降了69%。
在训练集中,当θ已知时,可以看到k近邻方法的估计精度同样也要优于经典核方法。随着样本量的增加,k近邻方法的改进幅度要大于经典核方法。在训练样本量为100时,相比于经典核方法,k近邻方法对应的平均均方误差下降了47%,在训练样本量为300时,下降了70%。
综上可以看出:k近邻方法基于样本本身自适应调整带宽,其表现要优于经典核方法,因为核方法的带宽是全局固定带宽,并不会针对样本本身进行自适应调整;同时k近邻方法的表现随着样本量的增加,估计效果相较于经典核方法提升明显。基于样本自适应调整带宽的k近邻方法依赖于样本本身,随着样本量的增加,其效果更优。
图2为k近邻方法与经典核方法在预测集的平均均方误差箱线图,考虑训练集样本量为200的情形,进行了200次独立重复实验。
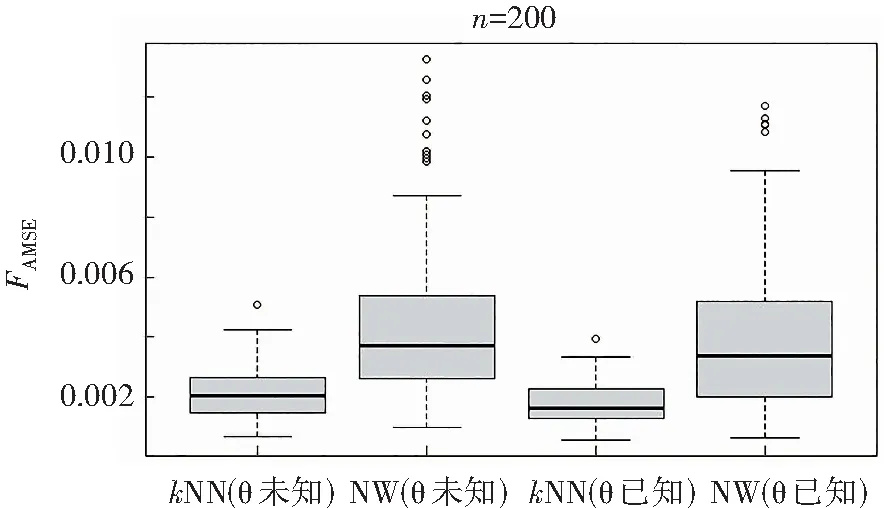
图2 kNN与NW预测集平均均方误差Fig.2 Mean square error of kNN and NW prediction sets
图2中,4个箱线图从左到右依次是θ未知时k近邻方法对应的平均均方误差,θ未知时经典核方法对应的平均均方误差,θ已知时k近邻方法对应的平均均方误差,θ已知时经典核方法对应的平均均方误差。
从图2左边两个图,可以明显看出:无论是θ未知还是已知,k近邻方法对应的平均均方误差均明显优于经典核方法,k近邻方法对应的平均均方误差要更集中且整体数值也要小;同时,在θ已知时,k近邻方法以及经典核方法对应的平均均方误差相较于θ未知时都得到了一定改善;无论θ已知还是未知,相比于k近邻方法,经典核方法对应的平均均方误差的离群值要多一些。
综上,在预测集上,从k近邻方法与经典核方法对应的平均均方误差的箱线图中,可以得到k近邻方法要优于经典核方法的结论。
图3为k近邻与经典核方法在训练集的平均均方误差箱线图,同样考虑是样本量为200的情形,进行了200次独立重复实验。
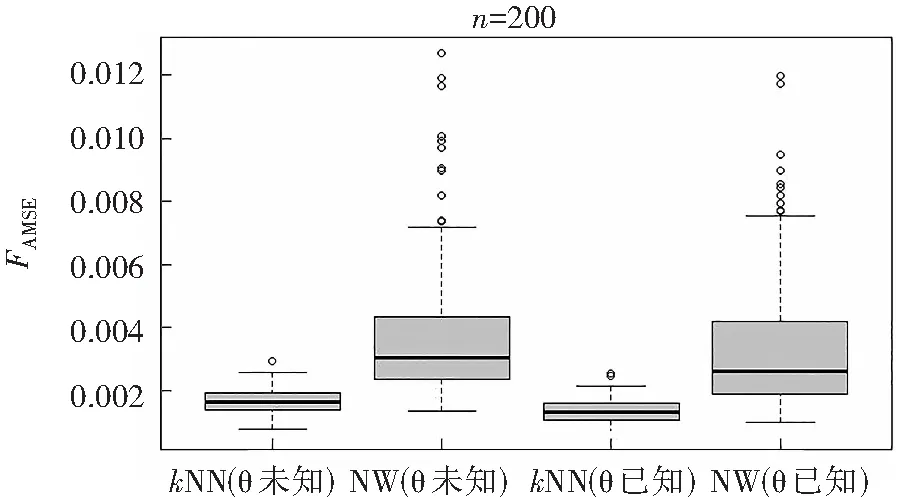
图3 kNN与NW训练集平均均方误差Fig.3 Mean square error of kNN and NW training sets
图3中,4个箱线图从左到右依次是θ未知时k近邻方法对应的平均均方误差,θ未知时经典核方法对应的平均均方误差,θ已知时k近邻方法对应的平均均方误差,θ已知时经典核方法对应的平均均方误差。
从图3可以看出:在训练集中,无论θ未知还是已知,k近邻方法对应的平均均方误差同样是优于经典核方法,k近邻方法对应的平均均方误差的集中性以及在数值大小上的表现与在预测集上一样优于经典核方法;无论θ是已知还是未知,k近邻方法的离群值要少于经典核方法。
综上,在训练集上,从k近邻方法与经典核方法对应的平均均方误差的箱线图中,可以得到k近邻方法优于经典核方法的结论。
图4为k近邻方法与经典核方法在训练集中估计效果的对比图,横坐标为真值,纵坐标为估计值,其中蓝色点为k近邻方法,黑色点为经典核方法,这里θ是未知的。从图中可以明显看出:k近邻方法估计效果要优于经典核方法,其对应点明显靠近y=x直线,即图4中红色的直线。

图4 kNN与NW 在训练集中比较Fig.4 Comparison between kNN and NW
4 实例分析
这部分进行实例分析,分析EL Nino地域(0~100 s,800~900 w),时间跨度为1982-01—2016-12的海平面月温度数据。数据来源:http://www.cpc.ncep.noaa.gov/data/indices/。本节的目的是利用真实数据比较k近邻与经典核估计的优劣,比较k近邻方法与经典核方法对真实数据的预测效果,同时采用与上一节模拟相同的随机缺失机制,对数据的处理方式参考Ling等[15]。
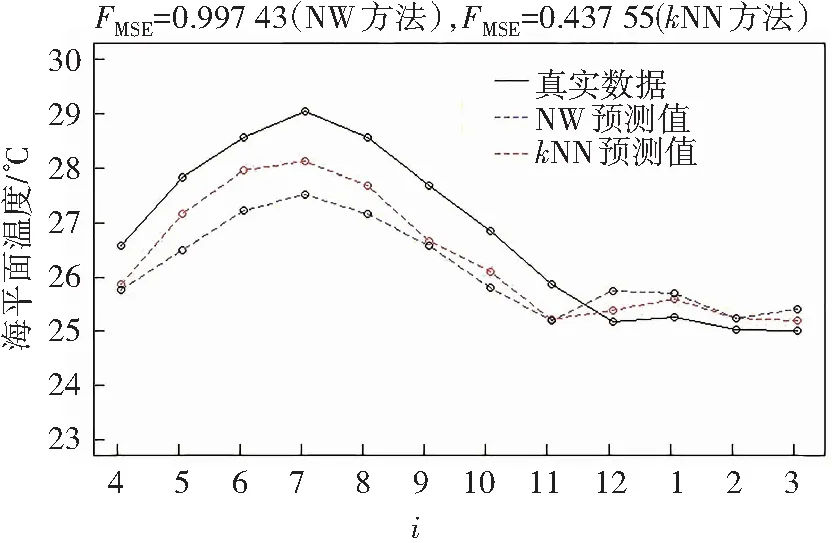
首先,将816个月的海平面月温度数据{zi,i=1,2,…,816}转化为函数型数据:将816个月的温度离散化数据分割成68a的温度曲线数据,将其表示为xi={vj(t),12(j-1)+4 图5 温度曲线Fig.5 Curves of temperature 响应实变量可以表示为Yi(s)={v12(j+s),s=1,2,…,12;j=1,2,…,67}。现在可以建立样本量为67的相依样本(xi,Yi(s))i=1,2,…,67,其中xi为函数型数据,Yi(s)为实值。 将67个样本观测值(xi,Yi(s))i=1,2,…,67分成两个部分,一部分是学习样本(xi,Yi(s))i=1,2,…,66用于建立模型,另一部分是检验样本(x67,Y67(s))。建模过程核函数的选取与数值模拟的核函数一致。 最后用k近邻方法和经典核方法预测第68个数据,结果如图6所示:红色折线为k近邻方法的预测值,蓝色折线为经典核方法的预测值,黑色折线为数据真值。 图6 kNN与NW预测比较Fig.6 Comparison between kNN and NW prediction 可以看到利用k近邻方法得到的均方误差(0.437 55)要小于经典核方法(0.997 43),在真实数据中,k近邻方法的表现同样保持优异。同时从曲线贴合度来看,k近邻方法优于经典核方法,即k近邻方法估计的预测值更接近于真实值。 从曲线的变化趋势上来看,k近邻方法也要优于经典核方法。气温在12月进入拐点,在这之后到3月气温保持相对平稳不变,虽然在11月和12月,k近邻方法和经典核方法预测的气温走势都与真实气温数据走势相反,但是在12月到1月以及2月到3月,经典核方法预测的气温走势与真实数据是相反的,此时k近邻方法预测的气温走势与真实气温数据一致,更能说明真实气温的走势情况。由此可以看出:k近邻方法预测的气温走势相比于经典核方法,更接近于真实数据。 在每个月份的估计效果上,k近邻方法都优于经典核方法,其中5月、6月、7月、8月优越性表现更为明显。 这说明k近邻方法用数据本身自适应调整带宽能够很好地改进估计效果及精度,相比于全局固定带宽的经典核方法表现要好很多。 经过上述分析可以看出:数值模拟中无论是训练集还是预测集,相对于经典核方法,采用k近邻方法可以明显改进估计效果,同时对于单指标θ的估计,k近邻方法比经典核方法要好,且随着样本量的增加,k近邻的提升效果要明显优于经典核方法。 从实例分析来看:k近邻方法在精确度以及稳定性上也都优于经典核方法,这说明采用k近邻对时间数据进行估计,其表现更加优异。这是因为核估计好坏主要受带宽的选取影响,k近邻方法基于数据本身,自适应调整带宽,可以更好地改进估计效果,而经典核方法采用的带宽为全局最优带宽,无法依托于数据本身进行自适应调整,对数据的适应性较差。从模拟和实例分析的结果来看:自适应调整带宽的k近邻方法的估计效果比经典核方法的估计效果要好。 综上可以得到:k近邻方法在响应变量随机缺失的时间序列单指标模型中表现优异,无论是模拟还是实例分析,其估计效果都明显优于经典核方法。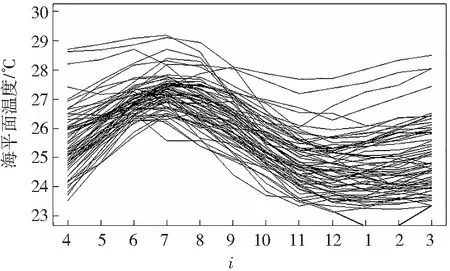
5 结 论

