基于自适应流形正则化自表示的无监督特征选择算法

宋 雨,许王琴,李荣鹏,宋学力,肖玉柱

长安大学 理学院,西安 710064

1 引 言

随着人工智能技术的突破和大数据时代的快速发展,各行业领域采集并储存了大量的高维数据。然而,高维数据中存在的大量冗余特征、无关特征和噪声增加了数据处理的复杂程度,带来了“维数灾难”问题,这给传统的数据处理方法带来了前所未有的挑战[1]。作为一种有效的数据降维技术,特征选择一般被用于高维数据的预处理过程中。在确保不丢失原始数据集中重要的特征前提下,特征选择通过相应的评价标准从原始特征集合中选择出一个满足条件的最优特征子集,以此来达到降低数据维数的目的,从而避免了由数据维数过高带来的一系列不利影响[2]。

根据数据集有无标签信息,特征选择方法可以大致分为有监督、半监督和无监督的特征选择方法[3]。在实际生活中收集到的高维数据大多数是没有标签的,而标签是指导模型搜索相关特征的重要信息。因此,无监督特征选择方法的研究相比于有标签信息的特征选择方法更艰难且充满挑战[4]。无监督特征选择方法一般会选择能保留与原始数据样本相似的全局或局部结构和包含判别信息的特征[5]。如何利用原始数据来发掘这些相似性结构和判别信息是研究无监督特征选择方法的关键。

基于自然界中物体的自相似性,即物体的一部分与自身的其他部分相似,有学者提出了基于自表示的方法并且应用到无监督特征选择算法中[6]。具体地,Zhu等[6]提出了基于正则化自表示的无监督特征选择算法(Unsupervised Feature Selection by Regularized Self-Representation, RSR),通过使用L2,1范数分别对表示残差矩阵和表示系数矩阵进行约束,抑制异常值对损失项的影响,有效地删除了冗余特征并选择了较为重要的特征;Zhu等[7]提出了非凸正则自表示的无监督特征选择算法(Non-convex Regularized Self-Representation for Unsupervised Feature Selection),选择L2,p范数(0≤p<1)对表示系数矩阵进行约束,从而获取更稀疏的自表示系数的解,取得了更有效的特征选择效果。由于Zhu等没有考虑样本空间的几何结构,可能会造成模型训练过程中样本的相似性结构发生变化,从而导致特征选择的效果不佳。针对这个问题,Liang等[3]受到流形学习的启发,提出了基于流形正则化自表示的无监督特征选择算法(Unsupervised Feature Selection by Manifold Regularized Self- Representation, MRSR),在目标函数中加入了对结构学习的流形正则化项,从而来选择出最具代表性且能保持局部结构的特征子集;Li等[8]提出了结合子空间学习和特征自表示的无监督特征选择算法(Unsupervised Feature Selection by Combining Subspace Learning with Feature Self- Representation),利用数据的性质构造自表示系数矩阵,通过稀疏表示寻找自表示系数矩阵的稀疏结构,并嵌入超图拉普拉斯正则化项来弥补普通图在多关系表示中的不足,从而优化特征选择的结果。上述算法均利用特征自表示的特性将特征的重要性表示出来,但忽略了重构过程中数据内部结构的变化。如果差异过大会进一步影响特征选择的效果。

流形正则化项要求原始空间中的相似样本应该在变换后的空间中依然保持接近,因此被广泛用于无监督特征选择中,构造出了一系列基于流形正则化的无监督特征选择算法。大多数现有的算法构造相似矩阵都是通过计算原始的样本空间中的相似性,并且在学习过程中是固定的。然而,样本的相似性矩阵构造不准确,这会导致特征选择的效果不佳。为了解决这一问题,Tang等[9]提出了基于对偶自表示和流形正则化的鲁棒无监督特征选择算法(Robust Unsupervised Feature Selection via Dual Self-Representation and Manifold Regularization, DSRMR),一方面使用特征自表示项来学习特征表示系数矩阵,以度量不同特征维度的重要性,另一方面使用样本自表示项来自动学习样本相似图,以保持数据的局部几何结构;Du等[10]提出了基于自适应结构学习的无监督特征选择算法(Unsupervised Feature Selection with Adaptive Structure Learning, FSASL),在模型训练过程中可以同时执行结构学习和特征选择,在保持样本结构的同时选择重要的特征;Zhang等[11]将相似矩阵的构造嵌入到优化过程中,与最大化类间散度矩阵的思想结合提出了自适应图学习和约束的无监督特征选择算法(Unsupervised Feature Selection via Adaptive Graph Learning and Constraint, EGCFS),从而选择出不相关但有区别的特征。相似矩阵的构造和约束是基于流形正则化的无监督特征选择方法的关键。自适应图学习的方法将相似矩阵的构造嵌入到优化过程中,不仅使图的相似矩阵自适应生成,而且使算法在每一步迭代中获取精确的数据样本的相似性结构,最终提高了算法的性能。从这些算法的结果中可以了解到,有流形正则化项的无监督特征选择算法的性能普遍比没有流形正则化项的算法要好,因为它可以帮助模型识别和保留了固有的几何流形结构。

MRSR算法采用文献[12]的方法,即学习的拉普拉斯矩阵在整个优化过程中是固定的,并且是在原始数据集上学习得到的,而在每一次迭代过程中,重构空间一直在发生变化。随着算法的迭代,如果在原始空间中学习到的样本相似性不准确,可能会导致算法的输出结果即选择的特征不理想。本文针对MRSR算法中样本的相似矩阵在重构空间中构造不准确的问题,将相似矩阵的学习嵌入到优化过程中,提出了基于自适应流形正则化自表示的无监督特征选择算法(Unsupervised Feature Selection Algorithm based on Adaptive Manifold Regularization Self-Representation, AMRSR)。设算法对相似矩阵施加了一个约束,即以更大的概率连接更近的数据点,不仅可以自适应地学习重构空间中的相似矩阵,而且可以获得相似矩阵的系数的闭式解[11],以较好地保持每一次迭代中重构空间样本间的相似性,从而选择出更具代表性且能保持数据几何结构的特征。

2 问题形式化

2.1 符号说明

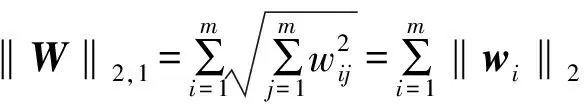
2.2 相关工作

特征选择算法通常将特征选择问题转换为一个多输出的回归问题[6],如式(1)所示:

(1)

其中,Y∈Rn×m是响应矩阵,W∈Rm×m是特征权重矩阵,L(Y-XW)是损失(Loss)项,R(W)是施加在W的正则化项,λ是正则化参数。

由于在无监督特征选择中很难选到一个合适的响应矩阵Y,依据特征的自表示特性,基于自表示的无监督特征选择算法一般使用数据矩阵X作为响应矩阵,即Y=X,可以理解为每一个特征都能由相关特征线性表示(包括它自身)。对于每个特征有

(2)

则对于所有特征有

X=XW+E

(3)

其中,W是特征自表示系数矩阵,E是表示残差矩阵。

RSR算法采用L2,1范数约束表示残差矩阵E,避免了Frobenius范数对数据异常值敏感的问题。此外,自表示系数矩阵W的第i行的值对应的是第i个特征在表示特征时的系数,那么‖wi‖2可以衡量第i个特征的重要性。如果‖wi‖2=0,表示第i个特征在重构其他特征时不起作用,则不选择该特征;如果某个特征参与了其他所有特征的重构,表示这个特征很重要,则选择该特征。那么,用L2,1范数约束表示系数矩阵W作为正则化项,可以获得一个行稀疏的表示系数矩阵W,用来衡量每个特征的重要性,起到了选择特征的效果。因此,RSR算法的模型如式(4)所示:

(4)

其中,λ1是正则化参数。

但此时,该模型忽略了样本之间的相似性结构,因为在重构空间中样本点之间的几何结构可能会发生变化。另外有研究表明,数据的内部结构其实接近于欧几里德环境空间的流形采样。所以在考虑数据结构时,数据的几何流形结构可能更能反映数据内部实际的结构状态[13]。为了能在重构空间中很好地保持原始特征空间中的样本相似性,通过利用拉普拉斯矩阵,将低维流形数据XW嵌入到拉普拉斯图中用于保持数据原始的几何结构。MRSR算法采用文献[12]的方法在原始数据上学习一个鲁棒拉普拉斯矩阵,并且在整个优化过程中一直保持不变。因此,MRSR算法的模型如式(3)所示:

(5)

其中,L∈Rn×n是拉普拉斯矩阵,λ是正则化参数。

3 算法模型优化

3.1 模型建立

MRSR算法的相似矩阵由原始数据推导出,并在后续过程中保持不变。然而,真实数据存在的异常值会造成相似矩阵不可靠,进一步影响低维流形数据XW的优化,最终导致特征选择效果不佳。

针对MRSR算法相似矩阵构造不准确的问题,将相似矩阵的学习嵌入到MRSR算法优化过程中,通过对相似矩阵施加概率最近邻约束,相当于以最近邻样本点相连接的概率衡量样本间的相似性,用于保持数据样本的局部几何流形结构,提出AMRSR算法,其模型如式(6)所示:

(6)

AMRSR算法不仅让重构空间中越接近的样本点以越大的概率相连接,以获得数据样本之间更清晰的相似性结构,而且通过自适应地学习样本的局部相似性结构进一步得到一个更加准确的拉普拉斯矩阵,进而在模型训练过程中保持更加精准的局部结构。系数γ可在优化过程中自适应生成,将在下一节详细介绍。

3.2 模型求解

采用交替迭代法对W,P和γ三个变量求解,求解过程具体如下:

(1) 固定P和γ,求解W。当P和γ固定的时候,变量W的解如式所示:

λTr(WTXTLXW)

(7)

(8)

则Wt+1的闭式解为

(9)

(2) 固定W和γ,求解P。当W和γ固定的时候,根据拉普拉斯矩阵的性质,如式(10)所示:

(10)

其中,F∈Rn×m并且f是矩阵F的列向量。那么,变量P的解可以写为

(11)

(12)

上式的拉格朗日函数可以表示为

(13)

其中,η≥0和βi≥0是拉格朗日乘子。根据Karush-Kuhn-Tucker条件和互补松弛条件,最优解pij如式所示:

(14)

(3) 固定W和P,求解γ。由于在无监督特征选择算法中,保持数据的局部几何流形结构比保持全局结构效果更好,所以只考虑k个近邻点来构造相似矩阵[14]。γ的最优解可以表示为所有γi的平均值。不失一般性,假设di,1≤di,2≤…≤di,n,因为pi满足pi,k>0≥pi,k+1,所以有

(15)

(16)

将式(16)代入式(15),有

(17)

最终将γ的值设置为所有γi的均值,给定当前估计值为Wt,则

(18)

将式(18)代入式(14),则

(19)

AMRSR算法的详细描述如下:

AMRSR算法输入:原始数据X∈Rn×m,参数λ,λ1,选择的特征数m1,选择的近邻数k初始化:t=0,Gtl,Gtr,Lt,γt重复以下步骤:(1)更新Wt+1=XTGtlX+λXTLtX+λ1Gtr()-1XTGtlX(2)更新Gt+1l,Gt+1r(3)按式(19)更新Lt+1=Dt+1-Pt+1=I-Pt+1(4)按式(18)更新γt+1直到收敛(5)计算特征权重‖wi‖2i=1,2,…,m()并且按降序排列输出:前m1个特征作为特征选择的结果

4 实验验证与分析

为了验证AMRSR算法的效果是否有提升,将其与其他几个经典算法在四个数据集上进行对比实验。通过将特征选择结果应用于K-means聚类对各算法的聚类结果(聚类精确度和归一化互信息)进行比较,所有算法的精确度和归一化互信息结果以及AMRSR算法的参数敏感性用图表展示。

4.1 数据集描述

实验共有4个数据集,包括control、JAFFE、ATT40和Yale。表1中详细介绍了这些数据集。

表1 4个公开数据集Table 1 Four public datasets

4.2 对比算法

MRSR算法:通过使用L2,1范数约束表示残差矩阵和系数矩阵,并且对重构样本进行流形正则化以保持重构空间中原始空间的样本相似性,以此来选择最具代表性且保持局部结构的特征子集[3]。

EGCFS算法:将相似矩阵的学习嵌入到优化过程中,使图的结构自适应,并且将最大化类间散度矩阵的思想集成到一个统一的框架中,以保持优异的结构,从而选择出更有效的特征子集[11]。

RNE算法:该算法基于L2范数作为损失项,首先通过局部线性嵌入算法获得特征权值矩阵,再用L1范数描述重构误差最小化,通过交替迭代乘子法来获取每个特征的权重,由此来得到最优的特征子集[15]。

LS算法:该算法用拉普拉斯分来评价一个特征的重要性,再根据分数选取最优特征构成特征子集,是一种经典的过滤式方法[16]。

MCFS算法:考虑不同特征之间可能存在的相关性,该算法通过聚类分析中的谱嵌入方法来尽量更好地保留数据的多簇结构。通过L1范数正则化来稀疏系数,从而能有效地进行特征选择[17]。

JELSR算法:通过局部线性逼近利用权值构造图,将嵌入学习和稀疏回归结合起来进行特征选择。通过添加L2,1范数正则化,学习一个行稀疏系数矩阵来进行特征排序[18]。

K-means算法:算法按照样本之间的距离大小来评价其相似度,即两个样本的距离越近,其相似度就越大,更有可能在一个类簇。在此过程中,不断更新聚类中心,最终把迭代求解出的紧凑且独立的簇作为聚类结果[19]。

4.3 参数设置

对于两个正则化参数λ和λ1,采用网格搜索法在{10-2,10-1,1,10,102}范围内设置,并记录所有算法的最佳结果。由于K-means聚类算法的初始类簇中心是随机生成的,所以将其执行10次,并且记录平均值,而其中的参数K为使用数据集的真实类别数[3]。control数据集所选特征数为{16,20,…,48},JAFFE、ATT40数据集所选特征数为{20,40,…,180},Yale数据集所选特征数为{20,30,…,100}。并且使用选择所有特征并执行K-means聚类作为基线。

4.4 评价指标

对特征选择结果用于K-means聚类,对聚类结果采用两种评价指标,即精确度(Accuracy,fACC)和归一化互信息(Normalized Mutual Information,fNMI),它们的值越大,说明算法效果越好。

fACC的定义如下:

(20)

其中,N是数据集的样本总数,yi和ci分别是样本点xi对应的真实类别标签和预测类别标签,δ(yi,ci)是一个示性函数,如果yi=ci,则等于1,如果不相等,则等于0[20]。fACC越高,说明特征选择效果越好。

给定两个变量P和Q,fNMI的定义如下:

(21)

其中,H(P)和H(Q)分别代表P和Q的信息熵,表示的是P和Q之间的互信息,则fNMI反映了这两个变量之间的相近程度[20]。对于本文算法,P和Q分别是聚类结果即伪标签和数据集的真实标签,fNMI越高,说明特征选择效果越好。

4.5 实验结果分析

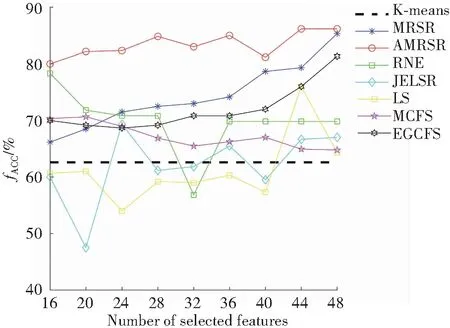
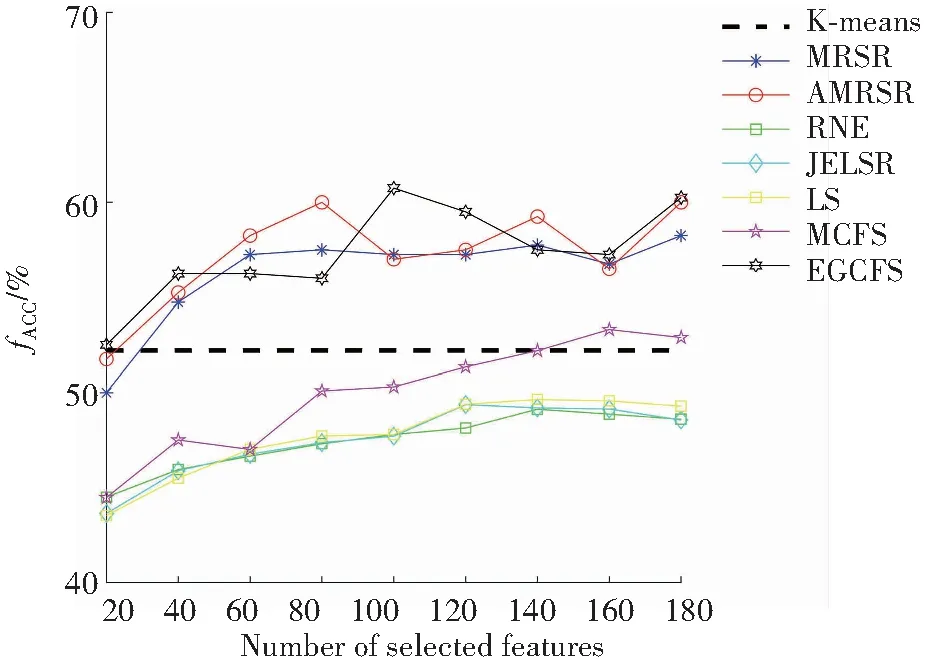
图1和图2分别展示了表1数据集上AMRSR算法和其余六种算法选择不同特征数时对应的最佳评价指标结果。图中横坐标表示的是特征子集的维数,纵坐标代表的是各算法的聚类精确度和归一化互信息。从图1和图2中观察到,当特征数目增加时,算法的聚类效果大多都是呈上升趋势的;并且在大多数情况下,AMRSR算法性能是有提升的,因为自适应流形正则化方法使得相似矩阵能够更好地反映重构空间数据结构,从而达到更好的性能。

(a) Control

(b) JAFFE

(c) ATT40

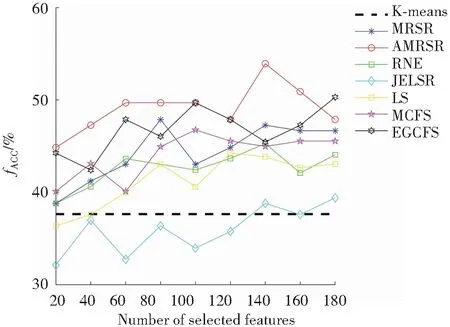
(d) Yale图1 在各数据集上选定不同数量特征时各算法的性能(fACC)Fig.1 fACC of each algorithm with different number of selected features on all datasets

(a) Control

(b) JAFFE

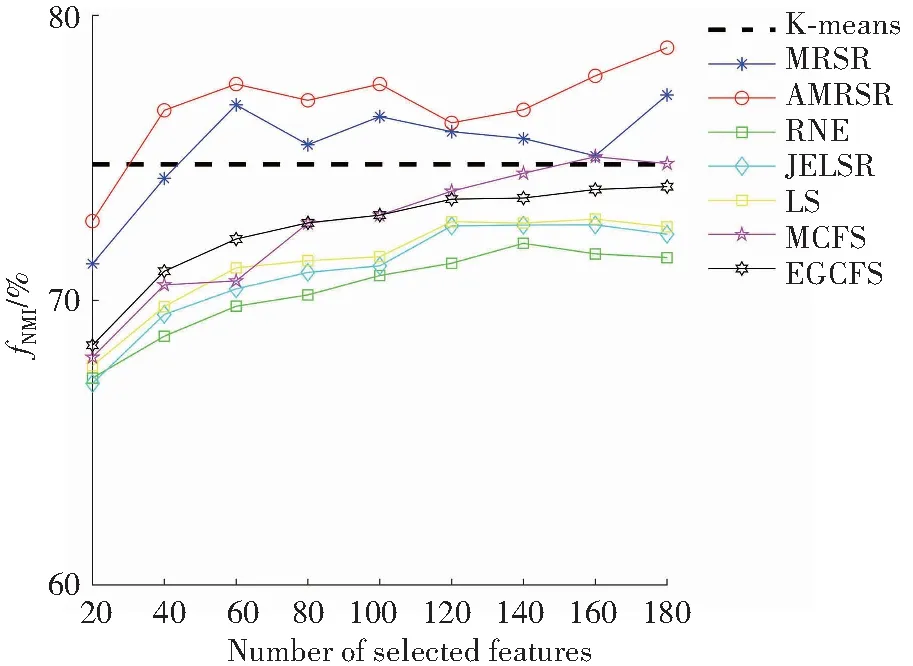
(c) ATT40

(d) Yale图2 在各数据集上选定不同数量特征时各算法的性能(NMI)Fig.2 NMI of each algorithm with different number of selected features on all datasets

表2和表3分别记录了各算法在数据集上对应的最佳评价结果,其中最优结果和次优结果分别由加粗项和点式下划线突出表示。与用原始数据集(所有特征)作K-means聚类结果(表格中的最后一行)相比,这些无监督特征选择算法不仅缓解了维数灾难,而且降低了数据处理的复杂度,更进一步提高了聚类性能。值得注意的是,该算法相比于MRSR算法,在聚类精确度上大致有1%～6%的提升,在归一化互信息上大致有2%～9%的提升。

表2 各算法在每个数据集上的最佳精确度Table 2 The best accuracy of each algorithm on each dataset

表3 各算法在每个数据集上的最佳归一化互信息Table 3 The best of normalized mutual information of each algorithm on each dataset

另外,在ATT40数据集上随机选取两个不同类别的样本来测试AMRSR算法是否能找到相关的有代表性且有区别性的特征,在它们的特征集合中分别选出20、40、…、180个特征,然后执行此算法。如图3所示,第一幅图是原图,然后依次为选择20、40、…、180个特征对应的人脸图,AMRSR算法选择的特征设置为白色。从图中可以看出,AMRSR算法倾向于捕捉人脸上有判别性的部位,如额头、眼睛、鼻子、嘴和脸颊等,这也进一步说明了AMRSR算法选出了更具代表性且利于分类的特征子集。

图3 AMRSR算法在ATT40数据集上的两个效果示例图Fig.3 Two sample graphs of effects of AMRSR algorithm on ATT40 dataset

4.6 参数敏感性分析

对于AMRSR算法,在实验中需要调整两个正则化参数λ和λ1。以control数据集为例,分别讨论了不同参数对结果的影响。当其中一个参数在设置的范围内变化的时候,另一个参数设置为1。图4展示了在该数据集上选择不同特征数时不同参数值对AMRSR算法的影响,其中横轴表示选择的特征数,纵轴表示参数的值。从实验结果可以看出,在control数据集上AMRSR算法对参数λ更敏感:参数λ值越大,结构学习的精度越高,选择的特征越能保持数据样本之间的结构,而参数λ1对该方法的聚类效果影响不大。

(a) 参数λ对聚类精确度的影响

(b) 参数λ1对聚类精确度的影响

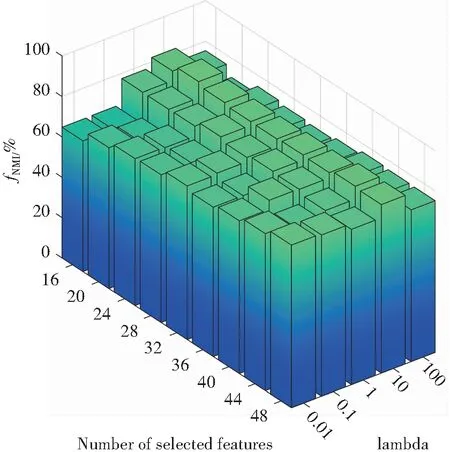
(c) 参数λ对归一化互信息的影响

(d) 参数λ1对归一化互信息的影响图4 control数据集上各参数对聚类精确度和归一化互 信息的影响Fig.4 Effect of parameters on clustering accuracy and normalized mutual information on control dataset

5 结 论

在基于流形正则化自表示的无监督特征选择算法的基础上,将相似矩阵的学习嵌入到模型训练过程中,在每次迭代中自适应地更新相似矩阵,以便于获取到更好的重构空间数据结构,进一步提高保持数据结构的准确性。重构表示系数矩阵即特征选择矩阵与相似矩阵相互优化,进而选择更具代表性且更能保持数据局部结构的特征子集。通过大量对比实验验证了基于自适应流形正则化自表示的无监督特征选择算法在聚类效果上优于现有的一些算法,这也进一步说明了该算法能选出具有更高精确度和归一化互信息的代表性特征子集。由于基于流形正则化的无监督特征选择方法关键点在于构造的拉普拉斯矩阵的质量,这直接取决于相似矩阵的构造。能否更加准确构造出数据样本的相似矩阵,是进一步探索的方向。