基于改进BVAR模型和MS-VECM模型的能源消费分析

王 星

重庆工商大学 数学与统计学院,重庆 400067

1 引 言

由Sim[1]提出的向量自回归模型(VAR)广泛应用于包括多元时间序列分析、货币政策效应分析等宏观经济研究中,但该模型只能包含有限的变量,在高维数据情形下会产生数据信息不全、误差增大、预测精度降低等问题。为了弥补这一缺陷,Koop等[2]提出将贝叶斯方法中的先验分布引入VAR模型中,从而建立贝叶斯向量自回归模型(BVAR)。先验信息为模型增加了额外的数据结构,使模型参数的不确定性降低并显著增强了样本外预测性能。然而,先验分布的具体选择和超参数的确定始终为该类模型的难点,对此,国内外学者提出了许多解决办法。

Litterman[3]在其研究中发现,在包含6个变量的VAR模型中应用贝叶斯收缩可以显著提高预测准确性;Miranda等[4]提出共轭先验分布同样能够有效地估计模型,达到极高的预测精度并在一般的宏观经济分析中表现出较好的性能。为了降低先验分布的主观性,Giannone等[5]利用分层建模思想,基于已有数据集,运用马尔可夫链蒙特卡洛(MH)算法提取先验信息;Carriero等[6]提出在正态-逆Wishart分布的前提下,利用模型系数的后验方差Kronecker结构和蒙特卡洛算法可以有效地模拟多步预测密度函数;Banbura等[7]从更实际的角度出发,考虑一组与能源消费变化关联性较强的变量,并在此基础上评估不同先验分布BVAR模型的泛化能力和有效性,其中正态-逆Wishart分布的表现尤其出色;而Sims等[8]同样发现将正态-逆Wishart先验分布与VAR模型相结合,经优化,其紧密性和滞后长度得出的BVAR模型符合预期。

尽管Banbura[7]和Sims[8]提出的BVAR模型展现了良好的效果,但当数据呈现高维情形时,模型难以在较多变量下保持准确估计。因此,本文考虑在传统VAR模型中运用贝叶斯收缩建立BVAR模型,其中先验分布根据具体研究问题由MH算法从以往数据集中提取超参数来确定,并且当变量增加时,通过设定与模型尺寸相关的收缩程度以保留相关样本信息的同时控制过度拟合。

另一方面,BVAR模型在实际运用中容易受到面板时间序列数据的制约,Fan[9]认为,这类数据不是一个线性随机过程,而是由时变、高阶矩结构、非对称周期等非线性动力学性质产生的,数据在时间序列中可能存在跳跃或断裂。为了使BVAR模型能够应用在时间序列分析中,Hamilton[10]提出的马尔可夫区制转移自回归模型是目前应用较广泛的选择,该模型可以较好地拟合数据出现跳跃或断裂的时间序列。Krolzig[11]将Hamilton模型推广到马尔可夫区制转移向量自回归模型(MS-VAR)和马尔科夫区制转移误差修正模型(MS-VECM),MS-VECM模型在估计变量受限模型框架的长期关系时更加灵活,并且由于该模型具有时变的动态特征,对市场变化的适应性更强。但在MS-VAR模型的基础上建立的MS-VECM模型仍然具有传统VAR模型的局限性,因此本文在改进的BVAR模型基础上,将MS-VAR模型推广为MS-BVAR模型,并基于该模型建立MS-BVECM模型。

为了验证改进后模型的有效性,本文以重庆市为例,研究其能源消费、产业结构升级和经济增长的动态关系,并对各项指标进行相关预测。

2 模型简述

2.1 传统向量自回归模型

向量自回归模型(VAR)是单变量自回归模型的推广,较后者能够更充分考虑滞后值之间的相互依赖关系,通常作为研究动态冲击效应的工具。有限p阶的VAR模型可表示为

yt=Ac+A1yt-1+A2yt-2+…+Apyt-p+εt

(1)

其中,t=1,2,…,T;AT=[Ac,A1,…,AP];εt～N(0,∑)为N×M维误差协方差矩阵。

若定义一个由截距项和滞后p阶的解释变量组成的矩阵

则式(1)可改写为

yt=ATxt+εt

(2)

VAR模型以伴随形式表示多步预测,即

(3)

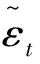
在高维情形下,高密度参数化导致维数灾祸的风险急剧上升,因此如何改进传统VAR模型,使其能在变量增加时,通过设定与模型尺寸相关的收缩程度以保留相关样本信息的同时控制过度拟合成为了关键。

2.2 先验分布的设定

为了处理向量自回归模型普遍存在的维数灾祸问题,引入先验信息概念,从而降维数据成为众多学者的选择。此处采用Kadiyala[12]和Robertson[13]的方法,为传统BVAR模型设置正态-逆Wishart共轭先验分布,即

A|∑～N(A0,∑⊗Ω0)∑～IW(S0,V0)

(4)

该分布保留了Minnesota先验分布的基本准则,同时,由于正态-逆Wishart先验分布为共轭先验分布,该模型的条件后验分布也为N-IW分布,即

(5)

其中,

以及

2.3 BVAR模型参数估计过程

概率转移函数为

β(xt+1|xt)=q(xt+1|xt)α(xt,xt+1)

接着,添加虚拟观测值来实现式(5),在式(3)中添加Td(Yd和Xd)虚拟观测值,将

S0=(Yd-XdB0)T(Yd-XdB0)T

以及V0=Td-k添加到正态-逆Wishart先验中。为了匹配Minnesota先验分布的维度,此处添加的虚拟观测变量形式为

现将式(6)代入式(3)中,以强化BVAR模型

(7)

其中,

需要说明的是,系数的后验期望与Y*对X*的回归OLS估计值一致。并从计算的观点来看,模型估计是可行的,只需求出维度为M=np+1方阵的逆矩阵即可。

2.4 MS-BVECM模型的建立

改进后的BVAR模型可以有效预测高维数据下能源消费和产业结构的动态关系,但却无力分析经济周期内各变量之间长期与短期均衡状态变化。当短期内经济变量受到波动而与长期均衡状态发生偏离时,误差修正模型机制会使其逐渐重新回到长期均衡状态,以保证模型的稳健性。但一般的误差修正模型无法具体描述短期均衡向长期均衡状态转移的过程,因此笔者考虑在以MS-VAR为基础发展的MS-VECM模型中进一步结合贝叶斯理论建立MS-BVECM模型。

若式(7)中的向量均为一阶单整向量,且向量之间存在协整关系,则将其变换可得到以下形式:

(8)

(9)

根据Hamilton[10]的方法,对上述误差修正模型加入马尔科夫区制转移特征,即对于可观测的时间序列向量yt,其潜在数据生成过程的参数依赖于不可观测的区制变量st,其中st∈{1,2,k,m}表示系统所处的不同状态,且

pij=P(st=j|st-l=i),∀i,j∈{1,2,…,m}

(10)

(11)

(12)

其中,μ(st)表示经济周期中不同阶段的增长率均值向量,即

μ(st)=[μ1(st),μ2(st),μ3(st)]T

例如:μ1(st),μ2(st)和μ3(st)可分别表示为重庆市能源消费增长率、地区生产总值增长率和产业结构转化率的条件均值。

3 实证分析

首先构造适当的虚拟观测先验分布,接着估计虚拟先验分布的参数并对其进行分层处理。需提出的是,这里不对先验参数α分层处理,因为该参数可以通过模式论证固定,一般情况下α=1,先验参数λ服从伽马超先验分布,之后运用MH算法时会为其算法所需的建议分布(此处为高斯分布)提供上界和下界。

对每个变量拟合p阶自回归模型后,自动设定先验参数ψ;接着,通过MH算法将确定的超参数分层处理后提供给虚拟观测先验分布,为建立BVAR模型提供条件。同时,为判断超参数是否达到平稳分布,需要知道其样本路径图,模型中选择的超参数包括lambda,soc和sur,经过优化后,以上3个超参数值分别为0.889 29,0.400 88,0.970 96,其中λ系数较大,说明模型可能会过拟合,因此参数数量应当缩减,如图1所示。(图1左侧图为轨迹图,右侧为概率密度函数度)可以看出:lambda、soc和sur是平稳的,没有漂移的情况发生,即可以认为3个超参数的马氏链构造是成功的,接下来便可以通过采集到的样本建立BVAR模型。

图1 边际似然和分层处理的超参数跟踪和轨迹图Fig.1 Hyperparametric tracking and trajectory plots for marginal likelihood and hierarchical processing

由表1可见:由于VAR模型中滞后阶数对协整检验和后续模型估计有一定的影响,所以根据LR、FPE、AIC、HQIC和SBIC这5种信息准则选定滞后阶数为5(Lag为滞后阶数,NA表示取值为空)。

表1 VAR模型滞后阶数选择Table 1 VAR model lag order selection

基于R软件进行平稳性检验和先验分布的选取以及滞后阶数确定之后,就可以估计并得到BVAR模型的参数,本文选取产业结构对数、能源消费对数和地区生产总值对数这3个指标即L=[lnVEC,lnVIS,lnVGDP]T建立BVAR模型,该模型以矩阵的形式可表示如下:

如图2所示,模型的残差都接近于0,说明其拟合程度较好,模型可用。重庆市能源消费、产业结构和地区生产总值对数时间序列的预测结果如图3所示,阴影区间分别表示90%置信区间和68%置信区间。

(a) 能源消费

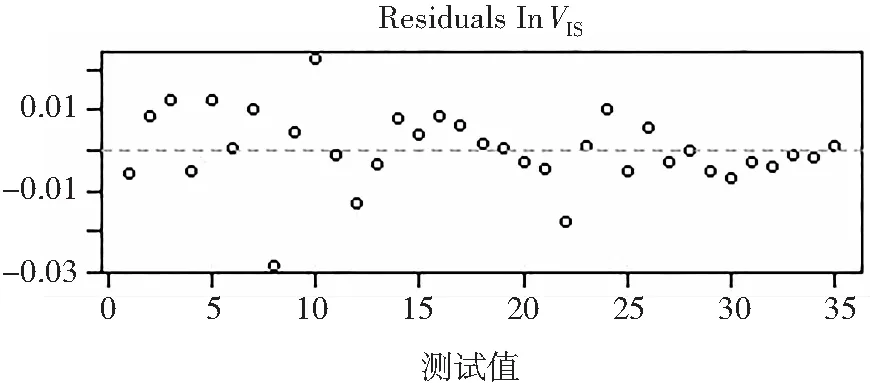
(b) 产业结构

(c) 地区生产总值图2 能源消费、产业结构升级和地区生产总值对数残差图Fig.2 Residuals of energy consumption, industrial upgrading and regional GDP

(a) 能源消费

(b) 产业结构

根据近5年能源消费增长率进行二区制划分,区制1(即st=1)表示平稳增长阶段,区制2(即st=2)表示快速增长阶段,并利用三元变量的MS2-VECM2模型描述不同增长阶段下重庆市能源消费和产业结构升级之间的动态关系。μ1(st)表示重庆市产出增长率过程中对应区制的条件均值,在区制阶段的限制下条件均值的参数约束为μ1(1)<μ1(2);μ2(st)和μ3(st)分别表示能源消费增长率和产业结构转换率在对应区制中的条件均值,其中能源消费增长率的区制划分依赖于产业结构转化率,所以能源消费增长率对应取值的条件均值没有参数约束。

在建立和估计MS-VECM模型之前,需要对重庆市能源消费、产业结构和地区生产总值进行平稳性检验,表2分别给出了以上3个指标的对数序列以及对数差分序列的ADF检验结果。结果表明:重庆市能源消费、产业结构以及地区生产总值的对数序列都是一阶单整过程,因此以上3个时间序列具有相同的单整阶数,可以在此基础上通过建立协整关系和误差修正模型来分析这3者之间的短期波动和长期均衡关系。

表2 ADF检验结果Table 2 ADF test results

已知向量yt=(y1t,y2t,y3t)T,表3给出了yt的Johansen协整检验结果,通过比较5%显著性水平临界值与迹统计量的大小,得出结果为拒绝“没有协整关系”和“至多一个协整关系”的原假设,接受“至多两个协整关系”的原假设,所以重庆市能源消费、产业结构和地区生产总值的对数序列之间存在两个显著协整关系,即长期均衡关系,说明重庆市能源消费、产业结构和地区生产总值之间具有相同的趋势水平。

表3 Johansen协整检验Table 3 Johansen co-integration test

随后,根据EVIEWS软件可估计得出协整方程为

et1=y1t-22.200 47y3t+9.150 286et2=y2t-39.664 61y3t+23.339 27

向量误差修正模型将偏离长期均衡关系的变量作为解释变量,对短期偏离的变量进行长期调节,因此该模型能同时描述短期调节过程和长期调节过程。并且该模型是在变量之间具有协整关系的基础上来体现不同经济时间序列之间的长期关系,以及短期偏离长期均衡的修正机制,所以具有较高的稳健性和准确性。模型估计结果如表4所示。

由表4可知:第一个协整方程3个误差修正项CE1分别为-0.163 298、0.166 208、-0.006 074,说明模型分别以-0.163 298、0.166 208、-0.006 074的速度对重庆市能源消费、地区生产总值和产业结构进行修正。第二个协整方程3个误差修正项CE2分别为0.107 606、-0.118 445、0.008 406,说明模型分别以0.107 606、-0.118 445、0.008 406的速度对重庆市能源消费、地区生产总值和产业结构进行修正。

得到变量的协整关系后,再假定式(11)中均值修正项μ(st)=[μ1(st),μ2(st),μ3(st)]T,具有状态转移性质的前提下,取式(11)中的滞后阶数p=5(该阶数由LR、FPE,AIC,HQIC和SBIC 5种信息准则得出),则所得MS-VECM模型为

图4和图5给出了能源消费在两个区制中的滤波概率估计。图4所示:1984—1996年,重庆市能源消费增长率开始出现区制1的运行特征,区制的取值概率接近于1,这意味着产业结构基本保持不变,同时经济增长基本保持平稳,能源消费基本处于“快速增长阶段”。1997—2006年,区制概率发生改变,此处是因为重庆成为直辖市后能源消费持续上升。图5表明此时重庆市能源消费正处于“平稳增长阶段”:2007—2011年,区制概率频繁发生改变,表明此时能源消费转变了平稳增加的状态,原因在于此时重庆市开始出台关于加快产业结构升级的若干政策,在产业结构升级的过程中能源消费增长率在逐渐降低。

图4 快速增长期的滤波概率Fig.4 Filtering probabilities for fast growth periods

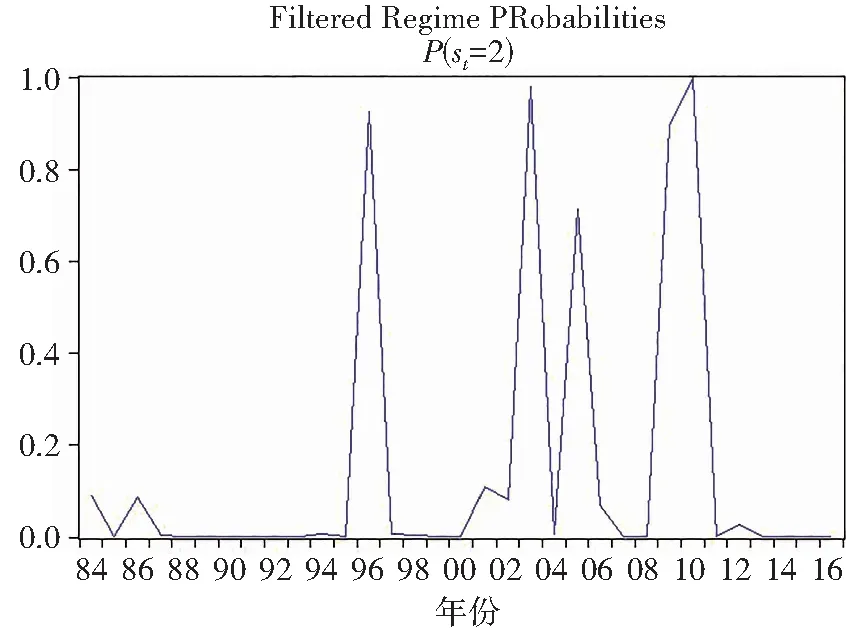
图5 平稳增长期的滤波概率Fig.5 Filter probabilities for a period of smooth growth

表5给出了能源消费时间序列中区制转移概率pij,当能源消费增长率处于“快速增长阶段”时,区制1的持续概率为0.958,这表明该阶段具有相当高的稳定性,主要原因在于重庆作为工业城市,在加速工业发展的同时必定会需要大量的能源消耗。从区制1转移到区制2的概率为0.042,从区制2转移到区制1的概率为0.038,这表明能源消费的阶段性转移具有一定的次序。当通过产业结构升级后,能源消费进入到“平稳增长阶段”,区制2的持续概率为0.962,这表明经过工业产业结构合理升级后,能源消费增长率大概率会持续在“平稳增长阶段”,但由于区制之间转移概率相差不大,一旦产业结构不合理便又会回到“快速增长阶段”。

表5 转移概率矩阵Table 5 Transfer probability matrix

4 结论与建议

4.1 结 论

针对传统向量自回归模型(VAR)的高维估计问题,结合贝叶斯理论,提出一种融合正态-逆Wishart共轭先验分布的估计方法并引入Metropolis-Hastings(MH)算法。从以往数据集中确定超参数收缩模型尺寸与传统VAR模型相比,基于贝叶斯理论的估计方法可在保留相关样本信息的同时控制过度拟合,具有较好的稳健性和有效性。此外,在改进的VAR模型基础上,结合区制转移技术与误差修正模型提出了MS-BVECM模型,该模型能够有效分析经济周期内各变量之间长期与短期均衡状态变化。最后,以重庆市能源消费为例进行了实证分析,主要研究结论如下:

(1) 通过MH算法将确定的超参数分层处理后提供给虚拟观测先验分布,并建立BVAR模型进行预测。预测结果表明:长期内重庆市产业结构升级和经济增长对能源消费增加有显著影响;短期内能源消费对经济增长有正向作用,但长期来说其对经济发展的促进作用有限。

(2) 通过平稳性检验和Johansen协整检验,得知重庆市能源消费、产业结构和地区生产总值的对数序列之间存在两个显著协整关系,即长期均衡关系,说明重庆市能源消费、产业结构和地区生产总值之间具有相同的趋势水平。

(3) 在协整关系基础上建立的MS-VECM模型(向量误差修正模型)表明:短期波动中,能源消费增长率与产业结构升级呈反向关系,与地区生产总值增长率呈正向关系,并且对能源消费和地区生产总值短期修正力度更大。

(4) 运用Hamilton模型中划分二区制的方法,将能源消费增长率划分为“快速增长阶段”和“平稳增长阶段”,通过建立区制转移模型得出结论:1984—1996年,重庆市能源消费增长率开始出现区制1的运行特征,区制的取值概率接近于1,这意味着产业结构基本保持不变,经济增长也基本保持平稳,能源消费基本处于“快速增长阶段”;1997—2006年,区制概率发生改变,原因在于重庆成为直辖市以后,能源消费明显增加;2007—2011年,区制概率频繁发生改变,表明此时能源消费转变为平稳增加的状态。

(5) 区制转移矩阵中,当能源消费增长率处于“快速增长阶段”时,该阶段具有相当高的稳定性,能源消费的阶段性转移具有一定的次序。当通过产业结构升级后,能源消费进入到“平稳增长阶段”,此时经过工业产业结构合理升级后,能源消费增长率大概率会持续在“平稳增长阶段”,但由于区制之间转移概率相差不大,一旦产业结构不合理便又会回到“快速增长阶段”。

4.2 建议

针对上述研究结果,提出建议:

(1) 致力于发展低碳技术,特别是煤的清洁高效净化技术,以及二氧化碳捕获与埋存等领域开发的有效控制碳排放的新技术。重庆市“十四五”时期是能源低碳转型进入碳达峰关键期,加大开展林业碳汇交易,研发出低价、清洁、高效和低排放的能源技术,对抢占低碳能源技术制高点,大力推进碳排放交易具有重要意义。因此,重庆市也应联合多方组织开展有关低碳经济关键技术的攻关,制定开发新型高效低碳技术的长远发展规划。

(2) 大力调整产业结构,尤其是工业内部行业结构。对于重庆市高能耗产业,例如电石、钢铁、铁合金等,可通过行业电价差别引导,实施惩罚性电价政策以整治高能耗产业。加大对重庆市落后产能的淘汰力度,降低节能损耗和推动循环经济,并打造新的低碳产业链。以往产业链的价值流向主要是资源型企业,发展低碳经济可打破目前流向:首先将由高碳产业引申出来的产业链条“低碳化”,接着通过逐渐降低高碳产业在国民经济中的比重,调整高碳产业结构,最终使重庆市国民经济的产业结构逐步趋向低碳经济的标准。

(3) 注重能源技术进步的长期发展以及持久研发,同时保持区制的自维持概率。短期内,行业能源技术的提高具有较强的跟风效应,但长期效应表现得并不明显。目前重庆市制度、市场和政策等条件虽然具备支持区制自维持能力,但企业技术进步的效应很难持久,缺乏长期、持久研发的动力。所以应加大对研发企业的补贴力度,增强企业研发的持久动力,保持重庆市快速经济增长过程的持续性和稳定性。