善用初等变换展开线性代数理论教学
欧阳毅, 张神星
(1.中国科学技术大学 数学科学学院,合肥 230026; 2.合肥工业大学 数学学院,合肥 230601)
0 引 言
线性代数学习中,初等变换是矩阵运算的基本操作方法,用中国科学技术大学线性代数教学的行语来说,就是“打洞”方法.它处于线性代数各类计算问题求解的核心位置.它起源于求解线性方程组的消元法,并被用来求方阵的行列式、可逆矩阵的逆以及更一般的矩阵方程AX=B的解、向量组中的极大线性无关组、整矩阵和域上多项式矩阵的Smith标准形、对称阵的相合标准形等[1-4].在理论推导中,可以通过运用初等变换来对矩阵进行降阶,从而使用数学归纳法来证明.在线性代数教学中,发现如果能够更灵活地使用初等变换,特别地,灵活运用初等变换的不变性质,不少线性代数核心结果的证明会比经典教材里的证明更简单.
本文基于这一观点,阐述如何系统而简洁地证明线性代数教学里下述重要理论结果:线性方程组求解的基本定理,行列式函数的积性,克莱姆法则,可逆的等价条件,矩阵相抵标准形定理,矩阵秩三种定义的等价性,整系数或域上多项式矩阵行列式因子的唯一性和Smith标准形的存在唯一性定理等.通过本文介绍的方法,教师可以在线性代数的教学中引入初等变换的思考方式,让学生更容易理解和应用线性代数的理论.这种“化繁为简”的思考方式可以帮助学生将抽象的问题转化为具体的行、列变换,从而更加直观地理解和解决问题.
近几年,本文作者在教学中采用了这种讲授方式,并取得了比较积极的反响和良好的效果.学生们通过实际操作和练习,逐渐掌握了初等变换的技巧和应用方法.他们发现,通过初等变换,原本复杂的线性代数问题可以被简化为一系列简单的步骤,从而更容易理解和解决.综上所述,通过引入初等变换的教学方法,可以让学生更容易理解和应用线性代数的理论.这不仅提高了教师的教学效果,也提高了学生的学习效果.因此,鼓励更多的教师在线性代数的教学中尝试使用初等变换的教学方法,以提升教学质量和学生的学习成果.
1 初等变换的核心结果
本文中,记In为n阶单位矩阵,记O为零矩阵,ej为第j个分量等于1而其它分量均为0的列向量 (它们的维度由上下文确定).除去文章最后一节,所有涉及的矩阵都是定义在某个域F上的矩阵.
先回顾一下初等变换的定义.
1.1 初等变换
定义1[1]矩阵的初等变换是指如下三类行或者列变换:
(i) 第一类初等变换:互换矩阵的两行或者两列;
(ii) 第二类初等变换:在矩阵的某行或者某列乘以一个非零常数;
(iii) 第三类初等变换:矩阵的某行或者列的常数倍加到另外一行或者列.
下面的事实十分简单,但在后面的论述中常常会遇到.
命题1初等变换是可逆变换,它的逆变换是同类型的初等变换.更确切地说,
(i) 第一类初等变换的逆就是它自己;
(ii) 第二类初等变换如果乘以的常数是λ,那么它的逆变换就是乘以λ-1(即除以λ);
(iii) 第三类初等变换如果加上的常数倍是a倍,那么它的逆就是减去a倍.
注1 因为初等变换是可逆变换,所以当证明初等变换前后两个集合相等或者两个量相等时,只需要证明两集合间的包含关系,或者两个量之间具有≤或整除的关系,而另外一个方向的结果就是显然的.这个方法在后面的证明中常常用到,不再做特别说明.
本文要初等矩阵的概念.
定义2[1]单位矩阵In做初等变换得到的方阵,称为初等矩阵.
(i) 初等矩阵Pij是互换In的第i,j行得到的矩阵,它也是互换In的第i,j列得到的矩阵.称Pij为第一类初等矩阵;
(ii) 初等矩阵Di(λ)是将In的第i行乘以λ得到的矩阵,它也是将In第i列乘以λ得到的矩阵.称Di(λ)为第二类初等矩阵;
(iii) 初等矩阵Tij(a)是将In的第j行的a倍加到第i行得到的矩阵,它也是将In的第i列的a倍加到第j列得到的矩阵.称Tij(a)为第三类初等矩阵.
下面两个定理是初等变换理论的核心定理.
定理1对m×n阶矩阵A做初等行变换相当于对A左乘对应的初等矩阵P,做初等列变换相当于对A右乘对应的初等矩阵P,其中P是对单位阵Im做同样的初等行变换(或者对In做同样的初等列变换)得到的方阵.
将命题1通过定理1翻译成矩阵语言,就有
也就是说:
推论1初等矩阵都是可逆矩阵.具体地说,即
定义3[1]若存在r≥1及1≤j1 uiji≠0 (1≤i≤r) 且uij=0 (i>r或者j 则称U是阶梯形矩阵,称uiji(1≤i≤r)为转角元,称r为台阶数. 如果阶梯形矩阵U的所有转角元都等于1而它们所在列的其它元均为0,即它的第ji个列向量是向量ei,称U是特殊阶梯形矩阵. 根据定义,显然有1≤r≤min{m,n}. 引理1台阶数r=n的n阶阶梯形方阵是主对角元全为非零元的上三角阵.台阶数r=n的n阶特殊阶梯形方阵只有一个,即单位阵In. 证这是由于1≤j1≤…≤jn≤n,故ji=i对于1≤i≤n成立. 下面的定理是初等变换的基本操作: 定理2任意非零矩阵A均可通过有限次初等行变换化为特殊阶梯形矩阵,且j1等于最小的列j,使得A在该列中有非零元. 翻译成矩阵语言,这个定理就是说 定理3设A是m×n矩阵,则存在m阶初等矩阵P1,…,Ps使得P1…PsA是特殊阶梯形矩阵. 假设本小节涉及的矩阵都是n阶方阵. 引理2若A是n阶方阵,P是n阶初等矩阵,则 det(PA)=det(P)det(A). 由此可知,若P1,…,Ps是初等阵,则 det(P1…PsA)=det(P1)…det(Ps)det(A). 证在P=Pij情形证明det(PA)=det(P)det(A),其余情形类似.一方面,PijA是将方阵A互换第i,j行得到的矩阵,根据行列式的基本性质,det(PijA)=-det(A).另一方面,根据行列式的定义,det(Pij)=-1.故det(PijA)=det(Pij)det(A). 定理4设A与B是同阶方阵,则det(AB)=det(A)det(B). 证由定理3,设A=P1…PsU,其中Pi是初等阵而U是特殊阶梯形矩阵. 如果U的最后一行全为0,那么det(U)=0.故由引理2得 det(A)=det(P1)…det(Ps)det(U)=0. 此时UB的最后一行也全是0,故det(UB)=0.再由引理2即得 det(AB)=det(P1…PsUB)=det(P1)…det(Ps)det(UB)=0. 所以在这种情况,有det(AB)=det(A)det(B). 如果U最后一行不全为0,那么m=n=r,故U=Im.此时A=P1…Ps,其中Pi为初等阵.故由引理2得 det(AB)=det(P1…PsB)=det(P1)…det(Ps)det(B)=det(A)det(B). 定理5下列条件等价: (i) 方阵A可逆,即存在B使得AB=BA=I. (ii)A的行列式det(A)≠0. (iii)A是有限个初等矩阵的乘积. 证(iii) ⟹ (i) ⟹ (ii) 是显然的,下面证明(ii) ⟹(iii). 设A=P1…PsU,其中Pi是初等阵而U是特殊阶梯形矩阵.由det(A)≠0知det(U)≠0,从而U的最后一行不全为0.故r=n,U=In.此时A=P1…Ps是有限多个初等矩阵的乘积. 注2 上述定理说明了求逆算法的正确性:若A可逆,总可以将(A,I)经过初等变换变为特殊阶梯形矩阵(I,B),此时B只能是A-1. 定理6(克莱姆法则) 设A是n阶可逆方阵,b=(b1,…,bn)T,Ai是将A的第i列用b代替后得到的矩阵.则线性方程组AX=b有唯一解 定理7设矩阵A经过初等行变换变为矩阵B. (i) 矩阵的行向量空间保持不变,从而A与B的行秩相等. (ii) 矩阵列向量组间的线性关系保持不变,从而A与B的列秩相等. (iii) 对任意1≤k≤min{m,n},B的k阶子式都是A的k阶子式的线性组合,从而A与B的秩相等. 证(i) 记A=(α1,…,αm)T,B=(β1,…,βm)T.若初等行变换是 (a) 互换两行,则{α1,…,αm}={β1,…,βm}; (b) 第i行乘以λ倍,则βi=λαi,αi=λ-1βi而βi′=αi′若i′≠i; (c) 第j行的a倍加到第i行,则βi=αi+aαj,αi=βi-aβj,而βi′=αi′若i′≠i. 所有情况都说明它们的行向量空间是同一个空间. (a) 若初等变换涉及到的行都在或者都不在集合{i1,…,ik}中,则 其中c=±1或者λ. (b) 初等变换为互换第i行与第j行,其中i∈{i1,…,ik}而j∉{i1,…,ik}.将集合{i1,…,ik,j}{i}中元素排序为i′1<… (c) 初等变换将第j行的a倍加到第i行,其中i∈{i1,…,ik}而j∉{i1,…,ik}.如同(ii)一样排序集合{i1,…,ik,j}{i}中的元素,则 同理,对于初等列变换则有 定理8设矩阵A经过初等列变换变为矩阵B. (i) 矩阵行向量组间的线性关系保持不变,从而A与B的行秩相等. (ii) 矩阵的列向量空间保持不变,从而A与B的列秩相等. (iii) 对任意1≤k≤min{m,n},B的k阶子式都是A的k阶子式的线性组合,从而A与B的秩相等. 推论3矩阵的列秩、行秩和秩三者相等.特别地,当矩阵通过初等变换化为阶梯形矩阵时,台阶数等于矩阵的秩是唯一确定的. 证根据定理7,只需考虑A是(特殊)阶梯形矩阵的情形,此时这是显然的. 推论5设A经过初等行变换变为特殊阶梯形矩阵U. (i)U的非零行向量构成A的行向量空间的一组基. (ii)A的第j1,…,jr列列向量构成A的列向量空间的一组基,即它们构成A的列向量组的一个极大线性无关组. 证(i) 这是由于A的行向量空间等于U的行向量空间,维数rank(A)等于U的非零行向量的个数,故U的这些非零行向量一定构成这个空间的一组基. (ii) 由于U的第j1,…,jr列列向量集合{e1,…,er}是U的列向量空间的一组基,而初等行变换不改变列向量间的线性关系,故A的第j1,…,jr列列向量集合组成A的列向量空间的一组基. 设A=(aij)m×n,b=(b1,…,bm)T,X=(x1,…,xn)T.考虑一般线性方程组AX=b的求解.不妨假设存在ai1≠0,否则变量x1就没有出现在线性方程组里面,其取值可以自由选择. 熟知需要对增广矩阵(A,b)做初等行变换.这里的关键在于: 引理3初等行变换不改变线性方程组的解集合. 证由于初等变换的可逆性,只需要证明变换前方程组的解都是变换后方程组的解,而这是显然的. (ii) 如果rank(A,b)=rank(A)=r,设X0是AX=b的一个解,VA是齐次线性方程组AX=0的解空间,那么AX=b的解集合等于{X0+Y|Y∈VA}. 注3 此处将A变为特殊阶梯形矩阵U,这让定理的结果可以写得更漂亮一些.当然在实际计算时,U为阶梯形矩阵就已经足够求解. (ii) 一方面若Y∈VA,则A(X0+Y)=b.另一方面,若AX=AX0=b,则A(X-X0)=0,即X-X0∈VA且X=X0+(X-X0). 满足等式Uβ=0.将其展开就得到djk=0对于1≤k≤r成立,故β=0.故VA是由{αj|j≠j1,…,jr}生成的线性空间.另一方面,{αj|j≠j1,…,jr}的线性无关性通过考虑它们的j分量(j∉{j1,…,jr}) 立得. 本节设R=或者F[x],其中F是域.环R与域有一个主要区别:R的非零元不一定是乘法可逆元而域的非零元都是乘法可逆元.事实上R的乘法可逆元集合R×即 R上矩阵的第一类初等变换和第三类初等变换与F上的初等变换没有什么不同.但对于第二类初等变换,对矩阵的某行或者某列同乘以λ倍,要使它为可逆变换,则需要λ∈R×.这样,在对R上的矩阵做初等变换时,不能任意除一个非零数得到1.需要用到R上的带余除法. 定义4设a∈R,称 为a的高度.若a>0(当R=时)或者a首一(当R=F[x]时),称a恒正. 引理4(带余除法) 若a,b∈R且a≠0,则存在唯一的q,r∈R,使得b=qa+r且h(r) 引理5设(a,*,…,*)与(b,*,…,*)是矩阵A的两行且a≠0.则经过有限次初等变换后可以将这两条行向量变为(d,*,…,*)与(0,*,…,*),其余行不变,这里d是a和b的最大公因子. 证这个引理实际上就是欧几里得算法的实现.不妨设(a,*,…,*)是A的第1行,(b,*,…,*)是第2行.设b=qa+r,则第1行的-q倍加到第2行,它就变为(r,*,…,*).若r≠0,令a=q1r+r1.则第2行的-q1倍加到第1行,它就变为(r1,*,…,*).继续这个过程,我们就将(a,b)变为(rn,0)或者(0,rn).再做一次第二类变换(使rn恒正)和最多一次第一类变换(将(0,rn)换为(rn,0)),(a,b)就变为(d,0),其中d是a和b的最大公因子. 定理10设A是R上的矩阵,B是A经过初等变换得到的矩阵.则对任意1≤k≤min{m,n},B的k阶子式都是A的k阶子式的线性组合.从而 (i)A的秩等于B的秩. (ii) 对于1≤k≤rank(A),则A的k阶行列式因子Dk(A),即A的所有k阶子式的最大公因子,等于B的k阶行列式因子Dk(B). 证只需证明Dk(A)=Dk(B),其余同定理7 (iii) 的证明.由于B的k阶子式都是A的k阶子式的线性组合,故Dk(A)|Dk(B).再由初等变换的可逆性,Dk(B)|Dk(A).故两者相等. 证(i) 首先证明存在性. (a) 由于A≠O,设aij≠0,互换第i行与第1行,再互换第j列与第1列,最后对得到矩阵的第1行乘以a11的符号或者首项系数的逆,这样最终得到的新矩阵A就满足a11恒正. (ii) 再证唯一性.由于初等变换不改变矩阵的秩,故r=rank(S)=rank(A).由于初等变换不改变行列式因子,故Dk(A)=Dk(S),但根据定义,Dk(S)=d1…dk,故 dk=dk(A)=Dk(A)/Dk-1(A). 注4 Smith标准形的唯一性在一般线性代数教材是使用更复杂的Binet-Cauchy公式证明的[1]. 另外,唯一性的证明还说明Dk-1(A)|Dk(A),这个事实也通过Laplace展开公式[1]得出,只要说明每个k阶子式都是k-1阶子式的线性组合即可. 定理12考虑R上的方阵.下列条件等价: (i) 方阵A可逆,即存在B使得AB=BA=I. (ii)A的行列式det(A)∈R×. (iii)A是有限个初等矩阵的乘积. 证(iii) ⟹ (i) ⟹ (ii) 是显然的.下面证明 (ii) ⟹ (iii).设A=P1…PsSQ1…Qt,其中Pi,Qj是初等阵而S是A的Smith标准形.由det(A)∈R×知rank(S)=n,S=diag(d1,…,dn)且det(S)=d1…dn∈R×.由于di恒正,这只能d1=…=dn=1,即S=In. 在线性代数的教学中,初等变换是一种非常重要的工具,可以用来证明线性代数中的定理与结论.通过使用初等变换,可以将一般的矩阵转化为性质已知的、结构简单的矩阵,从而证明各个主要结论和定理. 这种教学方式的优势在于,它能够帮助学生克服对线性代数中抽象理论的恐惧.相比于直接面对抽象的问题,将问题转化为具体的行、列变换可以使学生更容易理解和解决问题.这种直观的思路可以提高教师的教学效果,同时也能够提高学生的学习效果. 此外,通过使用初等变换进行证明,学生还可以同步地提高他们的计算能力.在进行初等变换的过程中,学生需要进行矩阵的运算和计算,这可以帮助他们巩固和提高他们的计算技巧.因此,这种教学方式不仅可以帮助学生理解线性代数的理论,还可以培养他们的计算能力. 总之,通过使用初等变换来证明线性代数中的定理与结论是一种有效的教学方法.它可以帮助学生克服对抽象理论的恐惧,提高教师的教学效果和学生的学习效果,同时还可以同步地提高学生的计算能力.因此,在线性代数的教学中,我们可以充分利用初等变换这一工具,来帮助学生更好地理解和应用线性代数的知识. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
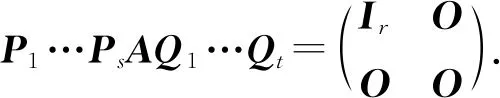
1.2 行列式的积性和矩阵的可逆
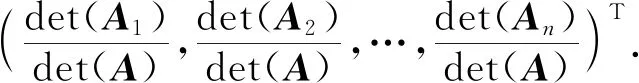

1.3 秩的三种定义的等价性
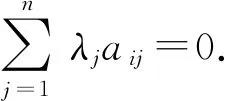


1.4 线性方程组的求解






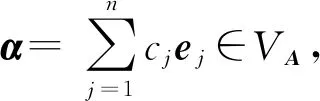

1.5 整系数和域上多项式系数矩阵的初等变换




2 结 论

