基于变分模态分解的新型材料齿轮故障诊断研究
张晓伟
(大唐山西新能源公司,山西 太原 030006)
1 齿轮故障诊断模型
1.1 VMD理论
VMD是一种自适应的信号处理方法,其将原始信号分解为具有稀疏特性的模态分量(intrinsic mode functions,IMF),同时每一个IMF都是基于中心频率和有限带宽滤波的信号[7]。VMD构造的约束变分模型为[8]:
(1)
式中:∂t为对时间变量t求偏导,δ(t)为单位脉冲函数,j为虚数单位,*代表卷积运算,uk为第k个模态分量,ωk为第k个模态分量的中心频率,f为信号。
引入惩罚因子α和拉格朗日乘子λ,将约束变分模型转变为非约束变分模型,即[9]:
(2)
式中:L()为增广拉格朗日表达式。
采用交替方向乘子算法能够得到鞍点,进而得到一系列的uk和ωk。
1.2 频带熵理论
频带熵(frequency band entropy,FBE)是用来表征频率成分随时间变化复杂性的量。采用短时傅里叶变换(STFT)计算信号时频分布图,根据FBE理论,通过信息熵指标选择最优频带[10]。由于STFT具有良好的带通滤波能力,因此在旋转机械设备故障诊断中具有十分广泛的应用[11]。采用STFT对信号进行分析,得到时频分布,即:
人的一生总要爱一些人,恨一些人,并从中找到自己存在的证明。爱他,就全力以赴去爱,恨他,就理直气壮去恨。且随它去,爱恨随心就是了。看到苦根那一头蓬乱的头发,雪萤便同情起这位老牛一样辛勤劳动却从未享受过生活的哥哥,这种同情化成了一种爱。而这种爱,指向一杭时便是一种恨。
(3)
式中:TER为时频分布矩阵;rM,C为信号强度;M为频率点数;C为在整个时间T内的傅里叶变换次数,C=N/L,N为信号采样点数,L为窗函数沿着时间轴移动的步长。
估算频率元素fk处的时间分布{rn,m},计算幅值谱熵,其数学表达式为:
(4)
式中:Hsk为频率元素fk处的频带熵,pm,k为概率密度,PX(fk)(Fm)为{rn,m}的幅值谱,Fm为幅值,X(fk)为在频率元素fk处的频率值。
频带熵表征的是信号在不同频带上的复杂度,常用于对信号结构和动态特征进行分析,其计算原理如图1所示。

图1 频带熵计算原理示意
通过计算信号在不同频带上的熵值,可以评估信号的质量、噪声水平和信息丰富程度。计算每一个频率分量的频带熵就可以得到全频带的各个频率分量的频带熵分布,即:
Hsf=(Hs1,Hs2,…,HsM)
(5)
式中:Hsf为频带熵分布。
1.3 故障诊断方法
采用传统的VMD方法提取早期机械设备故障特征是比较困难的[12],因此对VMD算法进行优化,达到有效识别故障信息的目的。VMD的惩罚因子α影响信号分解的精度,如果取值比较小,分解结果不精确;如果取值比较大,则会导致分解的时间比较长。与惩罚因子α不同,分解层数q直接影响分解的结果是否正确[13]。惩罚因子α选择默认值2 000,从希尔伯特变换出发计算峰度值来对分解层数进行优化,最终得到信号VMD的最佳分解层数q。考虑到最优分解层数q的一般取值范围,将分解层数q的搜索范围设定为2~15。假定实测信号VMD的层数为q,对得到的每一个IMF分量进行希尔伯特变换,得到每一个IMF分量的包络,即:
(6)
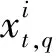
则第i阶IMF的包络峭度eq(i)为:
(7)

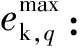
(8)
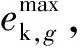
(9)
通过全局最大包络峭度值可以获得优化后的VMD层数。
对实测振动信号进行VMD,科学选择IMF分量是实施故障诊断的关键所在,采用FBE理论选择最优的IMF分量。对实测振动信号进行VMD,分别计算实测振动信号和每一个IMF分量的频带熵值,通过计算频带熵得到的一系列带通滤波器,也被称为特征频带间隔[14]。将所得IMF分量的特征频带间隔和原始信号的特征频带间隔进行比较,如果原始信号的特征频带间隔包含IMF分量的特征频带间隔,那么该IMF分量被认为是有效的IMF分量。如果VMD得到的多个IMF分量满足这一条件,那么将满足这一条件的所有IMF分量进行重构,得到用于分析的信号。对VMD进行优化,得到用于故障诊断的VMD模型,其故障诊断的具体流程如图2所示。
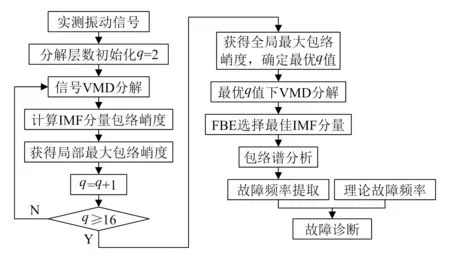
图2 改进VMD方法故障诊断流程图
2 仿真信号分析
2.1 仿真信号VMD
采用仿真信号模拟滚动轴承点蚀状态,设置模拟信号的采样频率为12 kHz,内圈故障频率为79 Hz,共振频率为3 000 Hz,得到模拟信号的波形图(图3),同时对模拟信号进行包络分析得到包络谱图(图4)。
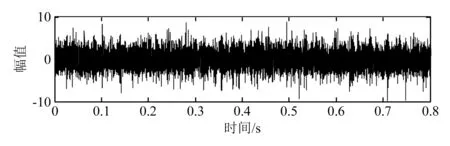
图3 模拟信号波形图
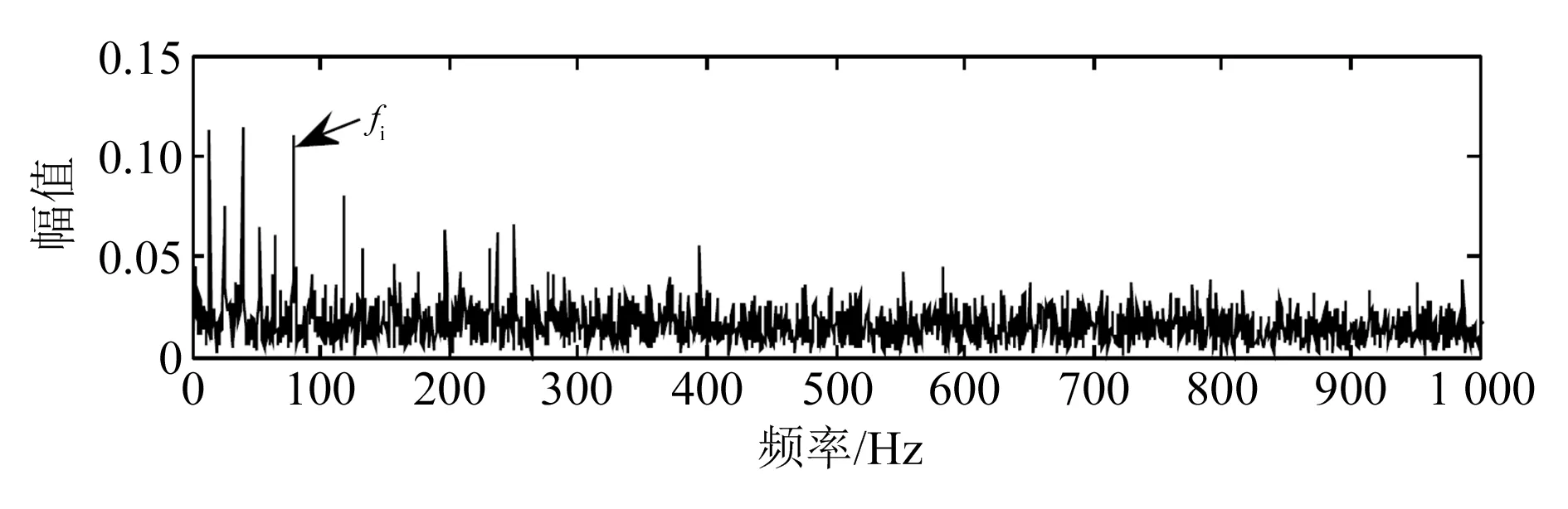
图4 模拟信号包络分析结果
采用VMD算法对模拟信号进行分解,初始化分解层数q=2,设定分解层数搜索区间为2~15。计算不同分解层数下的全局最大包络谱峭度,结果如图5所示。
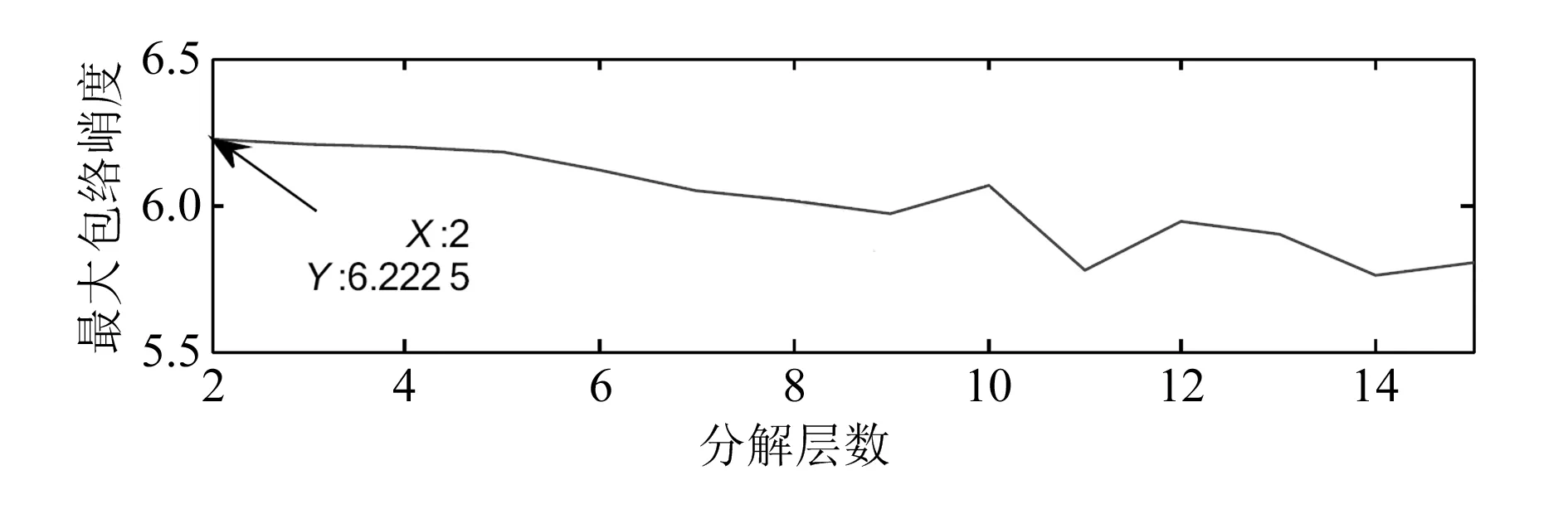
图5 分解层数和最大包络谱峭度关系图(仿真)
由图5可知,当分解层数q=2时,全局最大包络谱峭度值达到最大,因此该模拟信号最佳分解层数为2。
2.2 仿真信号最佳IMF选择
对模拟信号进行VMD,分解层数为2,采用FBE选择最佳的IMF分量。图6给出了模拟信号和各IMF分量的FBE值。
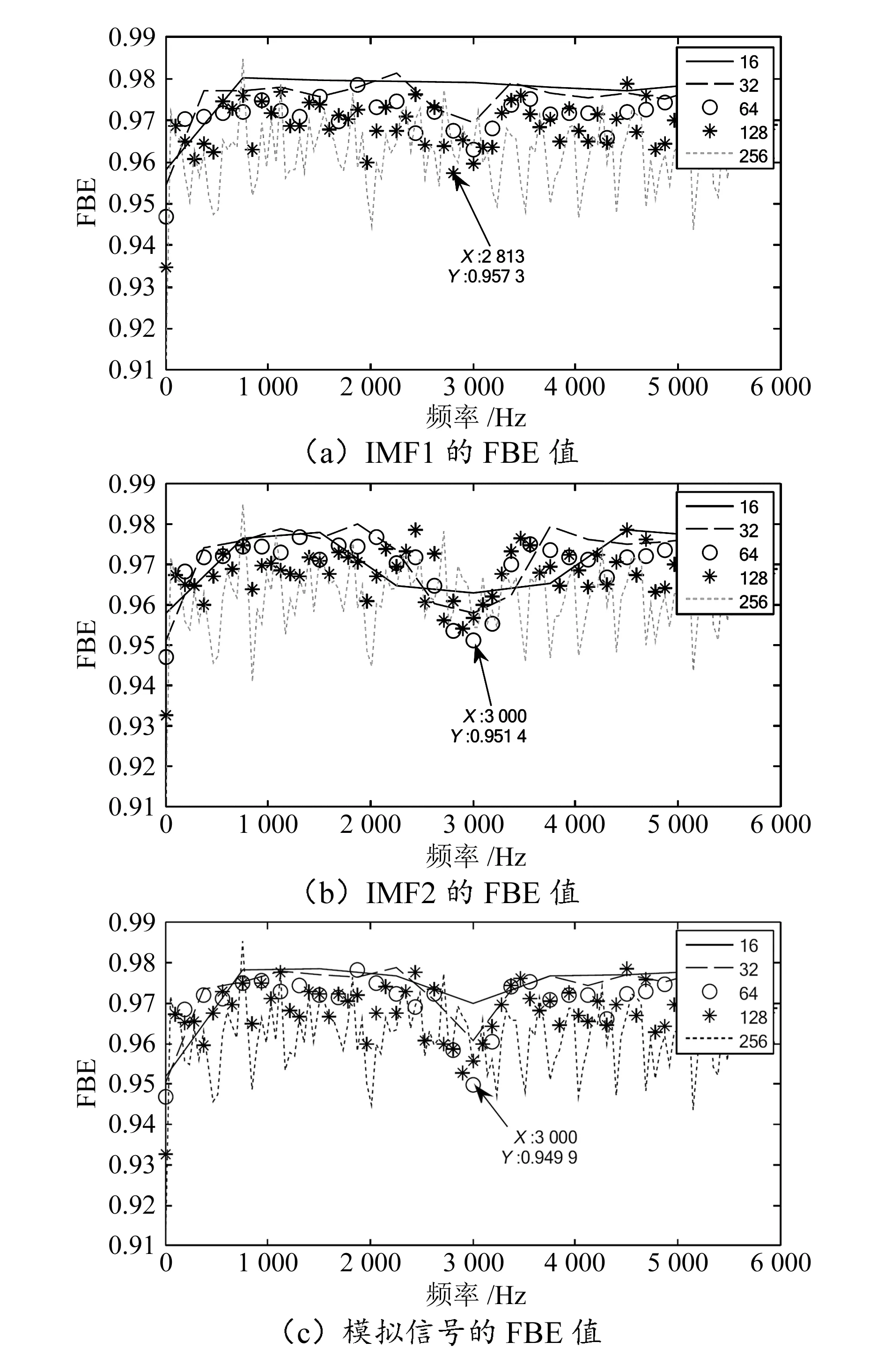
图6 模拟信号FBE分析结果图
IMF1特征频带间隔为[2 742.7,2 883.3],IMF2特征频带间隔为[2 859.4,3 406.6],模拟信号特征频带间隔为[2 859.4,3 406.6],因此选择IMF2作为故障诊断分析数据。对IMF2进行包络谱分析,结果如图7所示。
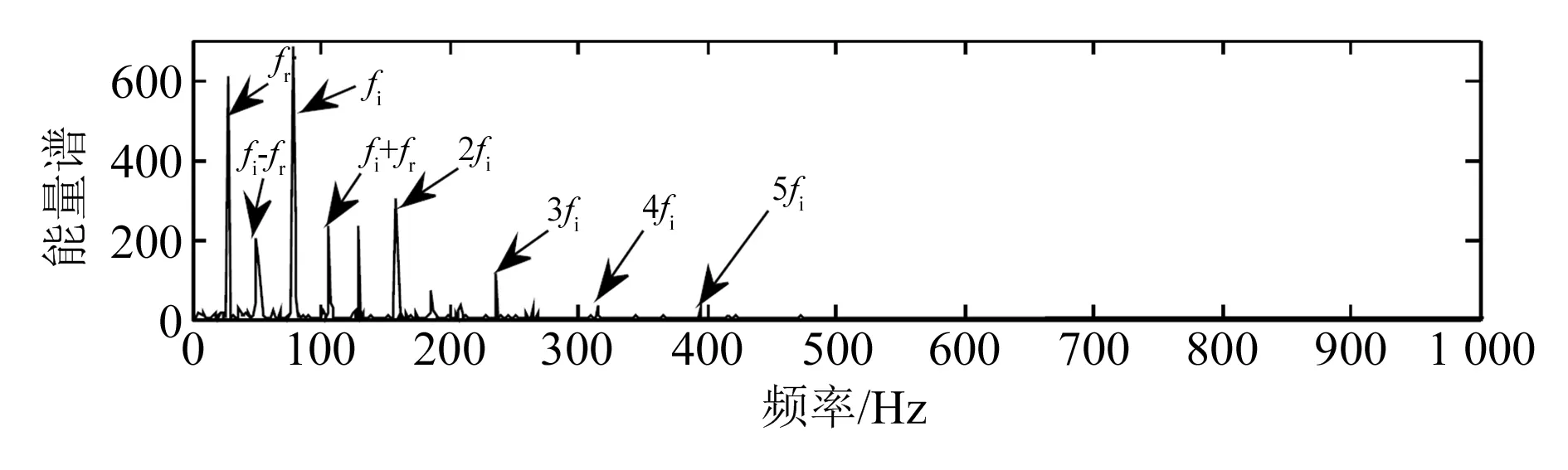
图7 IMF2包络谱分析
通过对比图4和图7可知,优化后的VMD在进行故障诊断方面更具优势。
3 实测故障信号分析
3.1 实测故障信号VMD
伴随着材料科学的快速发展,出现了多种新型材料,使得用于制造齿轮的材料种类也越来越丰富。高强度钢齿轮作为新型材料齿轮,在要求高承载能力与耐久性的作业环境中具有十分广泛的应用。如在汽车传动、风力发电、航空航天以及高速列车等领域具有十分广泛的应用。由于齿轮服役环境恶劣,同时一旦出现故障所造成的损失巨大,因此实施齿轮故障诊断至关重要。图8为齿轮故障模拟试验台3D模型,采用数据采集设备采集齿轮故障振动信号。
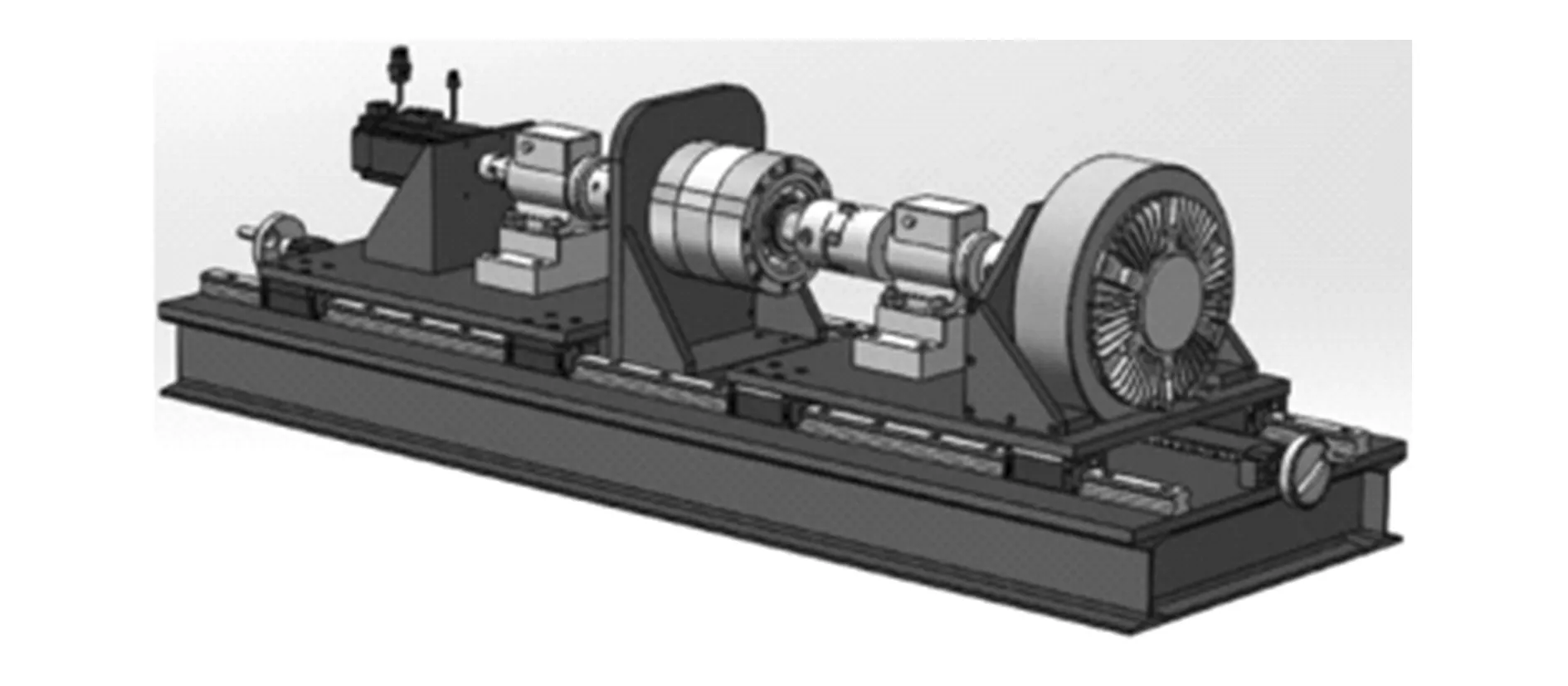
图8 齿轮故障模拟试验台3D模型
设定采样频率为12 kHz,得到实测故障齿轮振动信号波形(图9),同时对实测齿轮故障振动信号进行包络分析得到包络谱图(图10)。
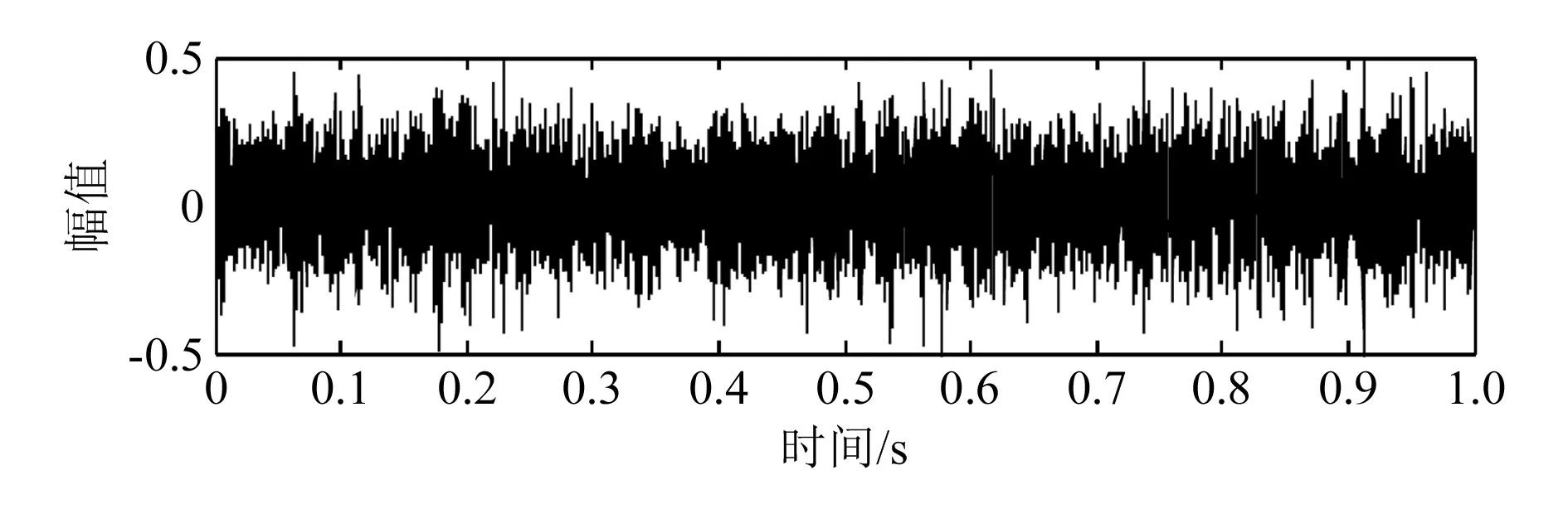
图9 实测齿轮振动信号波形
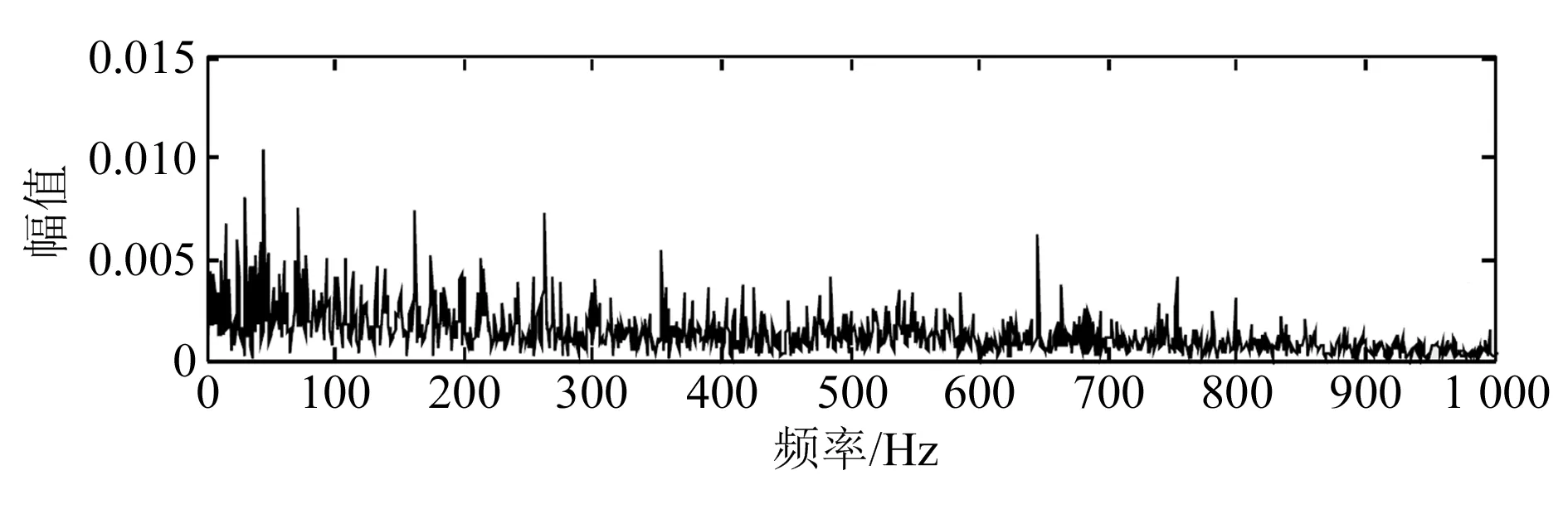
图10 实测齿轮振动信号包络分析结果
采用VMD算法对模拟信号进行分解,初始化分解层数q=2,设定分解层数的搜索区间为2~15。计算不同分解层数下的全局最大包络谱峭度,结果如图11所示。
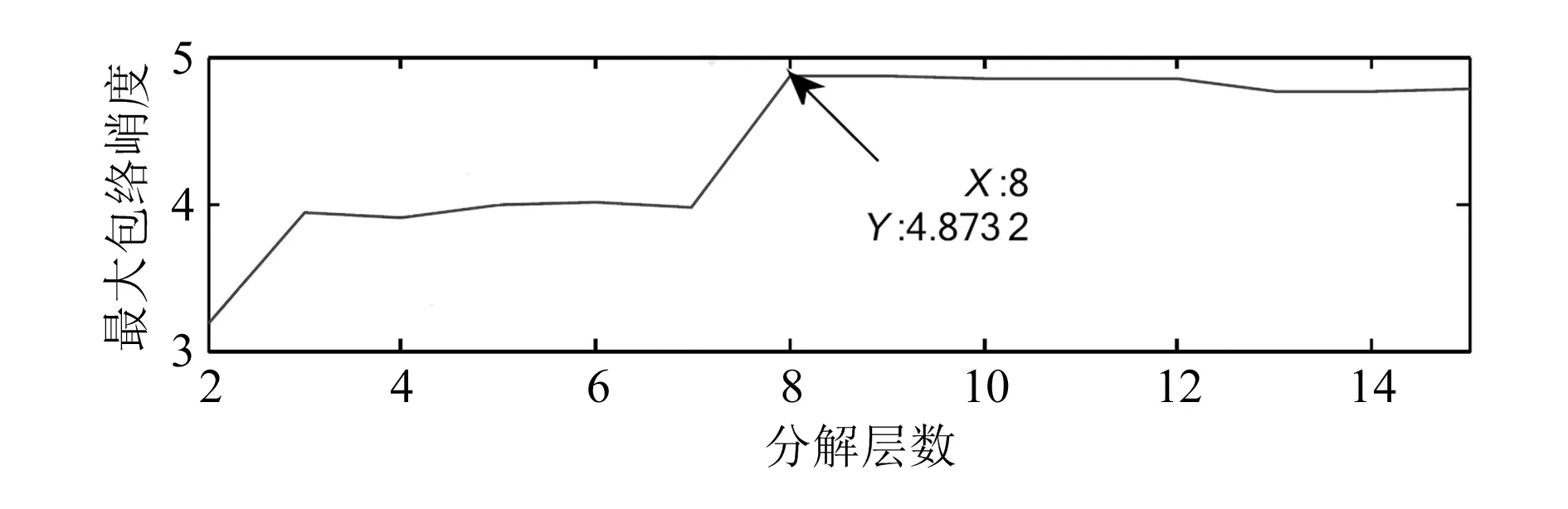
图11 分解层数和最大包络谱峭度关系图(实测)
由图11可知,当分解层数q=8时,全局最大包络谱峭度值达到最大,因此该模拟信号最佳分解层数为8。
3.2 实测故障信号最佳IMF选择
对实测齿轮振动信号进行VMD,分解层数为8,采用FBE选择最佳的IMF分量。分别计算实测振动信号的FBE值和8个IMF分量的FBE值,结合最佳IMF选择的标准,最终确定IMF4是最佳的IMF分量,其他的IMF分量不满足最佳IMF选择的要求。图12给出了实测故障信号的FBE值,图13给出了IMF4的FBE值。
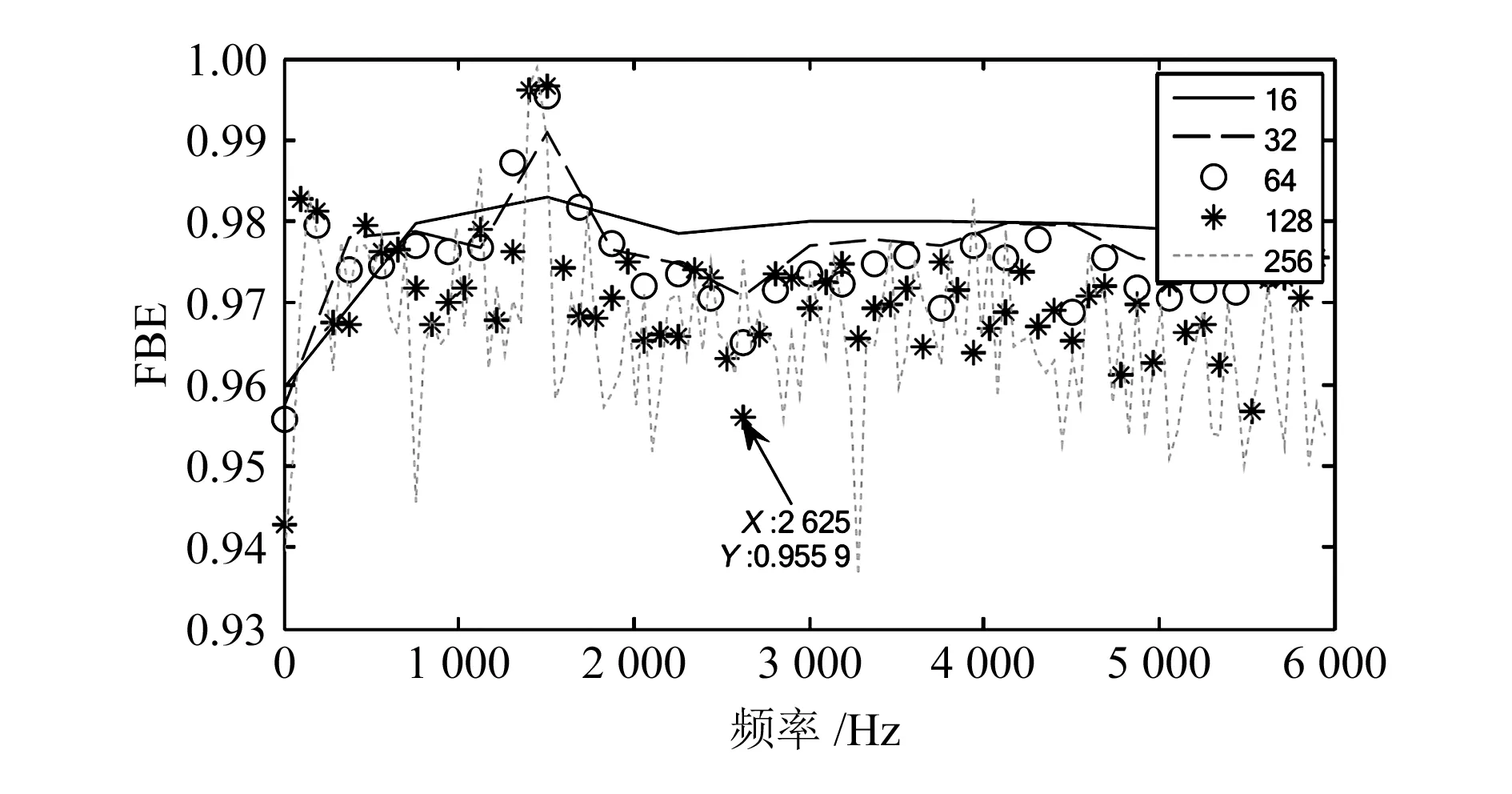
图12 实测故障信号FBE值
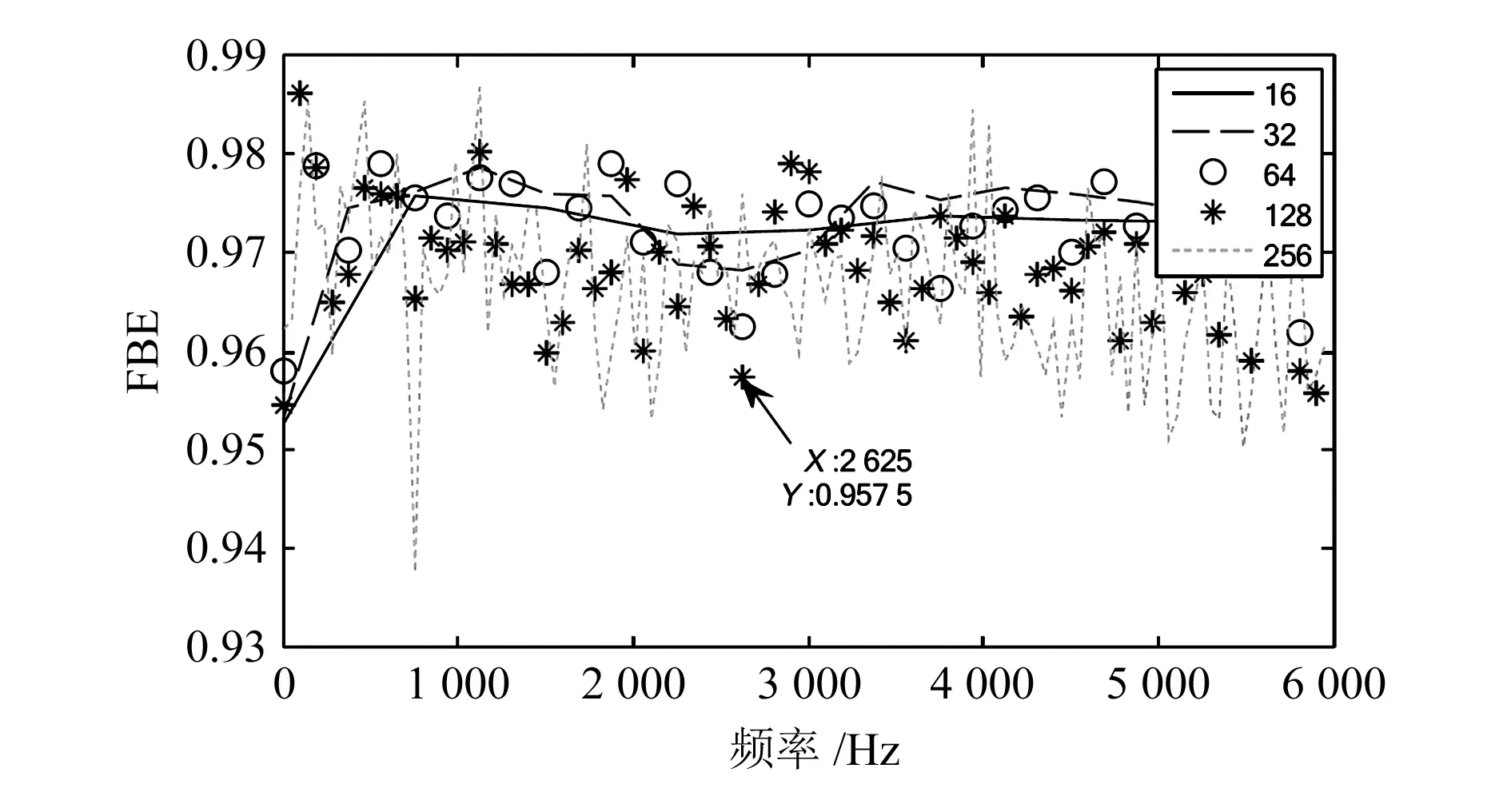
图13 IMF4的FBE值
选择IMF4作为故障诊断分析数据,对IMF4进行包络谱分析,结果如图14所示。
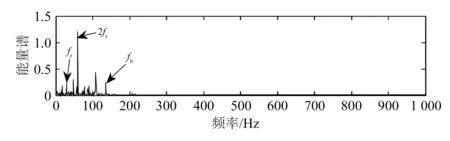
图14 IMF4包络谱分析
由图14可知,实测故障齿轮振动信号的故障频率fb、旋转频率fr和2fr被清晰地提取出来。
4 结束语
齿轮故障诊断与在线监测是提高机械设备运行可靠性、避免齿轮故障造成重大经济损失的有效措施。结合传统VMD存在的分解层数确定和IMF分量选择问题,提出了通过计算IMF分量包络峭度确定最佳分解层数和通过频带熵选择IMF分量的方法。将该方法应用于仿真信号和实测新型材料齿轮故障信号的分析、提取中,能够准确提取故障频率,对新型材料齿轮故障诊断具有一定的参考价值。

