齿轮齿条式前轮转弯机构的设计仿真和试验研究

孟 彬,胥海量,王春合

(庆安集团有限公司航空设备研究所,陕西 西安 710054)

操纵前轮转向已成为飞机地面转向的主要操作方式,使飞机转弯更加灵活,同时也避免了差动刹车导致的轮胎磨损和局部高温,即使在主起落架轮胎漏气的情况下依然能够操纵飞机。操纵前轮转向在军机如C141、C160、AN70、AN124、A225运输机和民机如ERJ170/190、ERJ135/145、F27、F50、F100、Bael146、ATR42、A320、A300、A310等客机中都得到了应用[1-3]。操纵前轮转向是通过一个集成到前起落架缓冲支柱外筒上的齿轮齿条机构实现的。为了减小齿轮齿条转弯机构的质量,本文运用啮合原理和轮齿啮合几何关系详细描述了齿轮齿条转弯机构修形的设计过程,并结合MSC.ADAMS/View对修形计算结果进行仿真,最后通过实物加工与试验验证了设计的正确性。

1 齿轮齿条转弯机构工作原理

齿轮齿条转弯机构如图1所示。在动力转弯角度范围内,在液压力作用下齿条带动齿轮及轮轴偏转至要求的角度。在牵引转弯状态下,转弯机构可适应轮轴的大角度范围偏转。当齿轮齿条机构处于动力转弯状态时,两作动筒分别接通进油和回油管路,接通进油管路的作动筒活塞推动齿条直线运动,齿条通过轮齿啮合带动齿轮平稳转动,如图2所示,此时转弯角度不大于60°;当齿轮齿条机构处于牵引转弯状态时,齿轮主动偏转,偏转角度不小于100°。在转弯角度小于脱开角度(脱开角度≤60°)时,齿轮通过轮齿啮合带动齿条直线运动,齿条两端的活塞随之运动,液压油在两作动筒之间循环流动,如图3所示。当转弯角度大于脱开角度时,为了减小齿轮齿条机构的行程和质量,齿轮齿条需脱开啮合,齿条及活塞静止不动;当齿轮回转至脱开角度时,齿轮齿条又可顺利进行啮合,因此需要对齿条的末端轮齿进行修形,如图4所示。齿轮齿条转弯机构修形结果如图5所示。

图2 齿轮齿条转弯机构功能原理图(动力转弯状态)

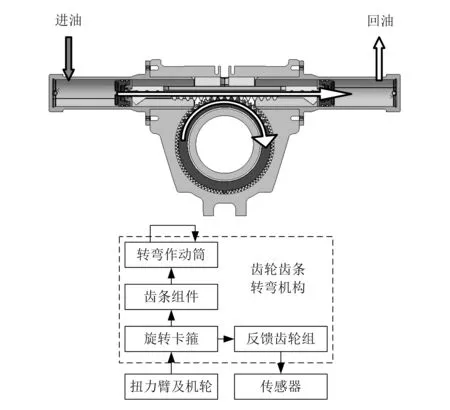
图3 牵引转弯状态(转弯角度<脱开角度)

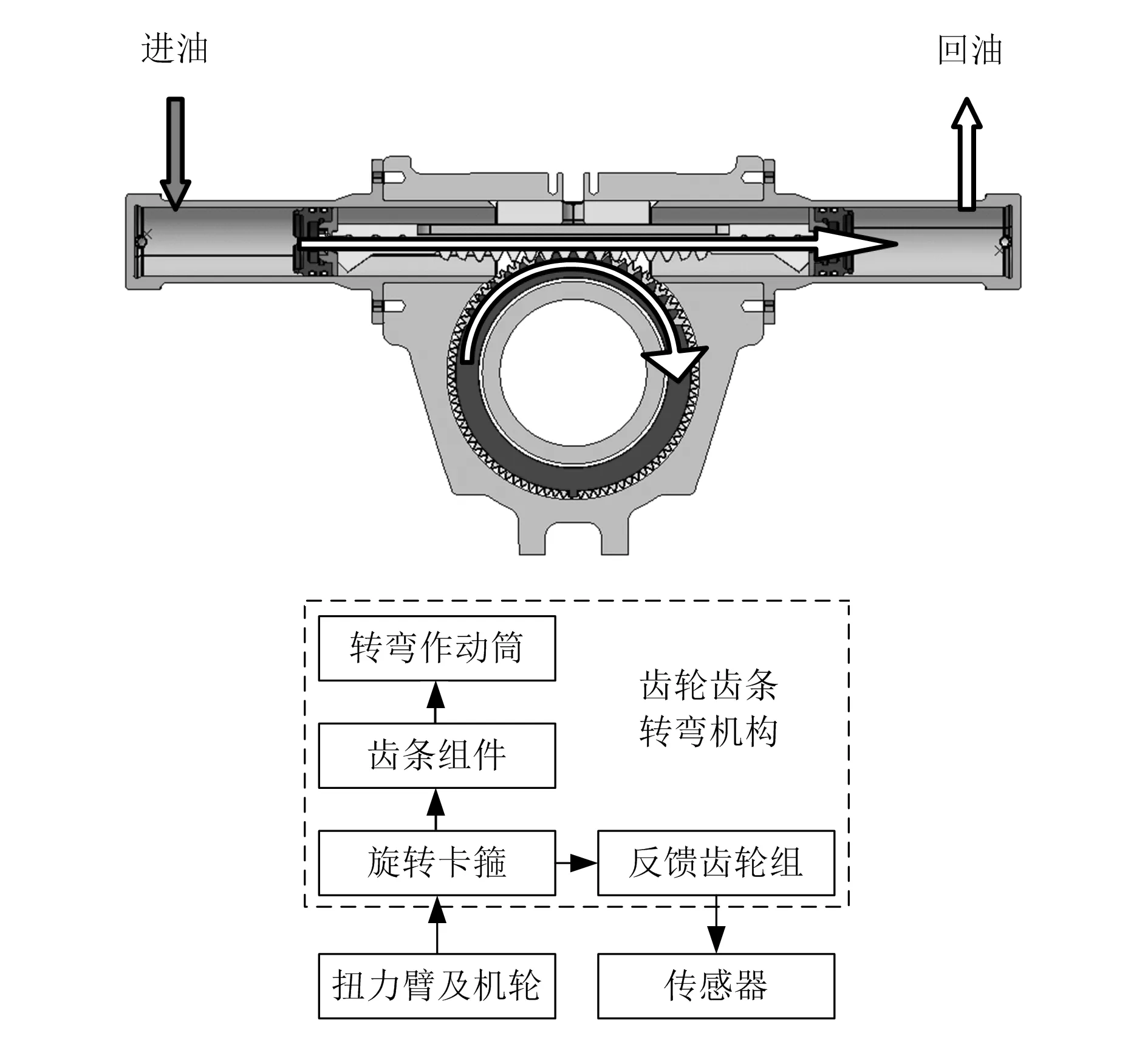
图4 牵引转弯状态(转弯角度>脱开角度)

图5 齿轮齿条末端轮齿修形图

2 各接触点高度的设计

动力转弯最大角度决定了最后参与共轭啮合的啮合点位置。显然,动力转弯状态(齿条主动)下,当齿条向右运动时,最后连续啮合的位置为图5中的S6处。牵引转弯(齿轮主动)时,齿轮齿条最后参与共轭啮合的位置为S1点。为了保证动力转弯角度不小于60°,S1点与S6点啮合时齿轮的旋转角度应大于60°。

牵引转弯状态下当齿轮上的S1点与齿条的S2点重合时,齿轮齿条完全脱开。为了减小齿条的行程,以最短行程设计S2点的高度。在动力转弯以及牵引转弯时,S4点一直处于共轭啮合中,为了确保在齿轮齿条脱开啮合前满足连续传动的重合度不小于1.2[4-6],先以重合度1.2为约束条件设计S4点的高度。各点的分布如图5所示。

2.1 以重合度1.2为约束条件设计S4点的高度

齿轮齿条共轭啮合连续传动时重合度ε的计算公式为:

(1)

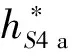
(2)

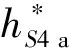
当齿轮齿顶S3点旋转到齿条上脱开点S4点时,齿条的轴向位移量L可根据图6所示的几何关系计算:

图6 脱开点S3与S4重合时齿轮齿条啮合图

L=6p+0.5s-(hS4-h)×tan(25π/180)+RasinθS4=109.81(mm)

(3)

式中:L为齿条的轴向位移量;p为齿条的节距;s为分度圆齿厚;Ra为齿轮的齿顶圆半径;θS4=arccos[(H-hS4)/Ra],其中H为齿轮的圆心到齿条基准面的垂直距离,H=107 mm。

2.2 以齿条行程最短为约束条件设计S1点处的齿轮半径和S2点的高度

设计S1点处的齿轮半径和S2点处的齿条高度时,以齿条相等的轴向位移量为目标函数,即当齿轮的S1点旋转到脱开点S2时,轴向位移量也为L=109.81 mm。

L=7p+0.5s-(hS2-h)×tan(25π/180)+RS1sinθS2=109.81(mm)

(4)

除等位移作为目标函数外,根据前轮转弯机构的性能要求,当S1点开始啮合时,齿轮的旋转角度不大于60°。此处为了使齿轮的质量最小,以60°为目标函数计算S1点的齿轮旋转角度αS1:

(5)

(6)

式中:Rb为齿轮基圆半径,θS1为齿条基准面垂线(过齿轮圆心O)与OS1连线的夹角,αS1为S1点齿轮的压力角。

联立式(4)～(6),求解可得:

(7)

在确定了S4点的高度后,为了设计加工的方便,将S2点的高度定为hS2=25.13 mm。

2.3 S8点的设计

在求出S4点的高度后,可根据图6及过S4点齿顶圆的切线与直线S8S9的交点确定S8点的高度。如图6所示的坐标系,X轴与齿条的节线重合,Y轴过齿轮的圆心,直线S8S9经过A点,A点的坐标为:

(RasinθS4+s/2-(hS4-h)×tan(25π/180),0)=(37.55,0)

(8)

则直线S8S9的方程为:

y=-2.14x+73.79

(9)

过S4点做齿顶圆的切线,切线方程为:

y=0.39x-10.59

(10)

则直线S8S9与过S4点齿顶圆切线的交点为(33.24,2.51),故S8点的高度为hS8=25.51 mm。

2.4 S6点的设计

求得S1点处齿轮半径和S2点处齿条的高度后可求得θS2。S1点在图6坐标系中的坐标为:

(RS1×sinθS2,hS2-h)=(20.07,2.13)

(11)

过S2点的切线斜率KS1S2为:

KS1S2=tanθS2=0.24

(12)

则过S2点且与齿轮上S1点处齿轮半径RS1的圆相切的切线方程为:

y=0.24x-4.82

(13)

直线S2S6的斜率KS2S6为:

KS2S6=tan(115π/180)=-2.14

(14)

直线S2S6经过点B,点B与图6中A点都是节线上的点,两点之间的距离为齿条的节距p。B点的坐标为:

(RS1sinθS2+s/2-(hS2-h)×tan(25π/180),0)=(21.84,0)

(15)

则直线S2S6的方程为:

y=-2.14x+46.84

(16)

过S2点且与齿轮上S1点处齿轮半径RS1的圆相切的切线与直线S2S6的交点坐标为(21.84,2.57),因此S6点的高度为hS6=25.57 mm。在实际加工时为了方便,S6点取与S8点一样的高度,即hS6=25.51 mm。

3 动力转弯状态下的最大旋转角度

3.1 S1点参与啮合时旋转角度的计算

齿条向左运动,节点P与齿轮圆心的连线与齿条运动方向垂直时,齿轮齿条的啮合点是S点,如图7所示。图中PB1为啮合线,OB1为基圆半径,OP为分度圆半径。由图7所示的几何关系,可求得OS=82.24 mm。

图7 连续传动初始基准(动力转弯)

S1点旋转角度的计算如下:

(17)

式中:φS1为S1点处的展角,αS、φS分别为基准点S的压力角和展角,ΦS1为啮合点S1点转动角度,RS为S点处齿轮的半径。

3.2 S6点参与啮合时旋转角度的计算

计算S6点的旋转角度时,有如图8所示的啮合示意图。

图8 齿轮齿条啮合示意图

已知S6点的高度,B1是啮合线与齿轮基圆的切点,O点是齿轮的圆心,OP为节圆半径。由图中的几何关系可以得出齿轮的啮合点为S6点时,压力角αS6为:

αS6=θS6OB1=21.42°

(18)

则S6点的旋转角度ΦS6为:

(19)

式中:θS6OB1为OS1连线与OB1连线的夹角,αS6、φS6分别为S6点处的压力角和展角。

通过计算,S1点啮合时的齿轮偏转角为62.67°,S6点啮合时的齿轮偏转角为62.11°,故齿轮齿条转弯机构连续转动的最大角度为62.11°,满足动力转弯角度在60°范围内都是连续传动的要求。

4 牵引转弯状态下完全脱开角度

齿轮齿条完全脱开角度是指齿轮副的传动比降为0时的瞬间齿轮偏转角度。因在实际工作中只会在牵引转弯状态时达到完全脱开,故只计算齿轮主动时的完全脱开角度。当齿轮齿条完全脱开时,此时的接触点为S2点,如图9所示。图中,C点为过齿条中心与齿轮中心连线上的点,S2点与齿条安装基准面的距离已知为hS2。与计算S6点压力角和展角的方法相同,S2点的压力角αS2与展角φS2如下:

图9 完全脱开时齿轮齿条机构位置

(20)

图9中其他角度的计算如下:

(21)

式中:φα为分度圆的展角,其他角度ΦBOC、ΦBOS2、ΦCOS2、ΦDOS2、ΦDOC如图9中所示。因此齿轮齿条完全脱开瞬间齿轮的偏转角为75.32°,齿轮齿条完全脱开时,齿条的位移量为:

L=7p+0.5s-(hS2-h)×tan(25π/180)+RS1sinΦDOS2=110.20(mm)

(22)

5 ADAMS仿真结果

MSC.ADAMS/View软件使用交互式图样环境和零件库、约束库、力库,创建完全参数化的机械系统几何模型,其中求解器采用多刚体系统动力学理论中的拉格朗日方法建立系统动力学方程,对虚拟机械系统进行静力学、运动学和动力学分析,输出位移、速度、加速度和反作用力曲线[7-10]。在MSC.ADAMS/View软件中建立齿轮齿条机构样机模型。在模型中,分别在齿条下端添加部件,并在齿条与部件间添加接触,用来模拟齿轮齿条运动过程中齿条所受到的外部阻力。仿真时,各个部件之间的约束关系见表1。在动力转弯状态下,在齿条上添加速度为100 mm/s的驱动,使其沿地面做平行移动,同时带动齿轮转动;在牵引转弯状态下,在齿轮上添加驱动,使齿轮在10 s内完成运动。

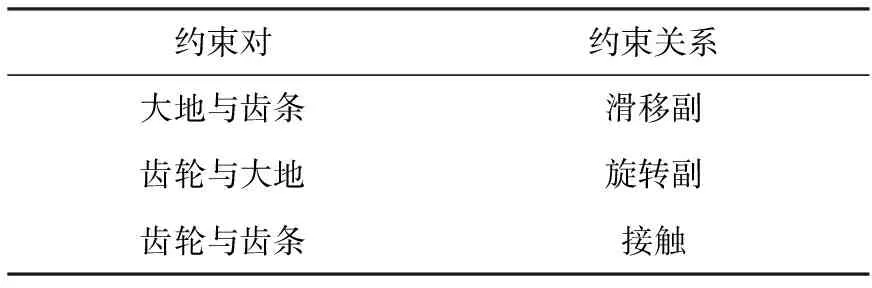
表1 约束关系

图10所示为动力转弯时齿轮旋转角度的理论值与仿真结果对比,由对比结果可得齿轮连续转动时转动的角度为62°～63°。

图11所示为牵引转弯时齿轮旋转角度与齿条移动位移关系图,由图可知,当齿轮齿条脱开时齿轮相对于零位转过的角度为75.89°,齿条相对于零位的位移为110.05 mm。

图11 牵引转弯时齿轮旋转角度与齿条位移关系图

6 实物加工与试验验证

齿轮齿条转弯机构的实物与试验台如图12所示,试验时首先让试验件处于动力转弯状态(在旋转卡箍输出端施加载荷,作动筒分别接通进油/回油),使产品在中间位置的[-60°,60°]范围往复运转3个循环,观察旋转卡箍的运转平稳性,再单方向驱动齿条直至出现旋转卡箍角度非连续传动,记录旋转卡箍转动的角度,如图13所示,得到动力转弯非连续传动时的角度为64°。再将试验件调至牵引转弯状态(将进油/回油转弯作动筒的油路相互沟通),驱动旋转卡箍的输出端,使旋转卡箍在[-100°,100°]范围内运转,观察齿条的运动,记录齿条静止不动瞬时的旋转卡箍偏转角度及齿条位移量,如图14所示,得到牵引转弯脱开角度为78°,位移为109.5 mm。

图12 齿轮齿条转弯机构与试验台实物图

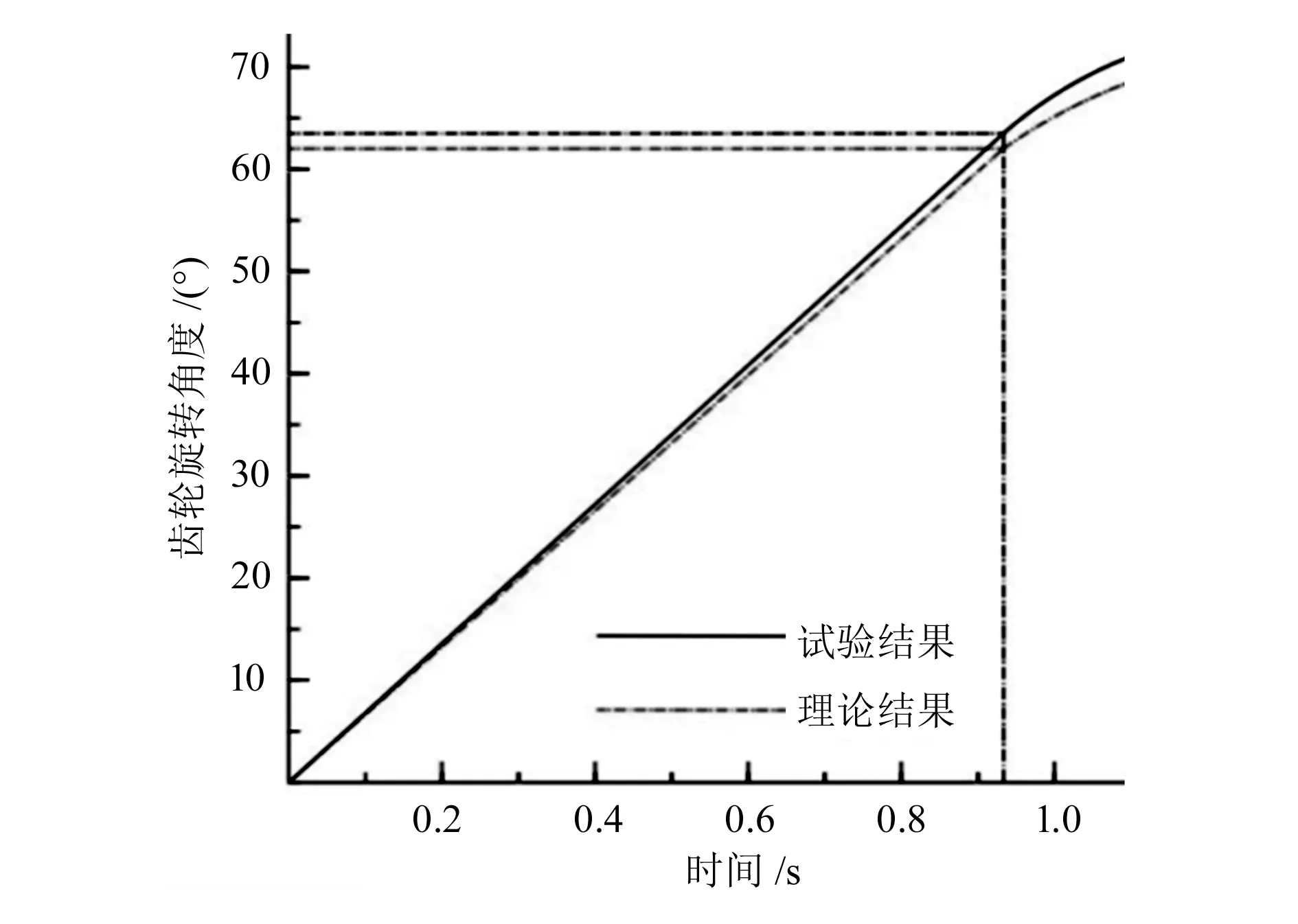
图13 动力转弯时试验台齿轮旋转角度

图14 牵引转弯时试验台齿轮旋转角度与齿条位移关系图

7 结束语

本文针对飞机起落架前轮转弯机构齿条末端齿进行修形设计,首先以共轭啮合连续传动重合度最小1.2为目标设计S4点高度,再以齿条行程最短为约束条件设计S1点处齿轮半径和S2点的高度,最后以过S4、S2点的直线方程求出S8、S6点的高度。结合齿轮齿条转弯机构进行仿真分析以及加工实物进行试验验证,得出齿条末端两个齿进行削齿设计后,可以满足动力转弯状态下齿轮连续传动角度为62°～63°,大于60°。牵引转弯状态下,齿轮齿条完全脱开时转动角度为75.89°,大于动力转弯角度,即齿轮在脱开啮合与进入啮合时可以保证齿与齿不干涉,齿条位移为110.05 mm。仿真结果与理论计算结果的误差小于1%,经分析知误差主要来源于理论计算时对数据进行了圆整;试验结果与理论计算结果的误差小于3%,经分析知主要是理论计算时未考虑齿侧间隙及加工误差、装配误差等引起的传动误差。由以上分析可知,理论计算结果正确,对齿条的削齿设计能够满足工作要求。