复杂深孔内轮廓数控加工误差在位修正技术

张欢唱,冯亚洲

(1.汉中职业技术学院汽车与机电工程学院,陕西 汉中 723002)(2.西安石油大学机械工程学院,陕西 西安 710065)

复杂深孔内轮廓数控机床(以下简称数控机床)在加工过程中[1-2],刀心和刀轴在机床高频率振动和旋转的影响下,会出现不同程度振动和偏离情况[3],导致复杂深孔零件内轮廓出现误差,加工后的零件无法应用。针对上述情况,已有多位学者进行了相关研究。例如白振华等[4]提出了离线板测量误差修正方法,通过分析数控离线板误差形成机理,建立数控离线板重力影响模型,使用悬挂测量方式修正数控机床轮廓误差。但该方法在应用过程中,存在数控离线板重力数值不够精准,导致最终的数控机床轮廓误差修正效果不佳。宋碧芸等[5]提出齿轮曲面加工误差修正方法,以复杂深孔加工时钻孔刀具与零件之间相对关系为基础,建立钻孔刀具和加工零件之间的曲面函数关系,计算复杂深孔内轮廓误差数值,利用 Levernberg-Marquardt算法计算轮廓误差量,并输入数控机床控制器内,实现深孔内轮廓误差修正。但该算法在计算轮廓误差量时,受参数选取影响,导致轮廓误差量精度不足,适用性较差。面对当前复杂深孔内轮廓误差修正技术存在的不足,本文研究了数控加工误差在位修正技术,以提升数控机床加工复杂深孔零件的技术水平。

1 复杂深孔内轮廓数控加工误差在位修正技术

1.1 数控机床运动学模型构建

以加工复杂深孔零件的五轴数控机床为例,构建运动学正解模型和逆解模型,利用这两种模型获得该数控机床的刀心方位坐标和刀轴运动方位。

1)数控机床运动学正解模型。

令a1、b1、c1、d1、e1表示数控机床刀轴进给的5个运动方位,将这5个刀轴运动方位坐标转换为矢量矩阵Ψ[6-7],其计算公式如下:

Ψ=Trans(pa1,pb1,pc1)×Rot(d1,-e1)×Rot(b1,-d1)×Trans(-a1,-b1,c1)

(1)

式中:(pa1,pb1,pc1)为数控机床加工刀具的切削点坐标,Trans(·)表示坐标系转换函数,Rot(·)表示向量旋度函数。

构建数控机床加工刀心方位矩阵:

(2)

式中:(Qa1,Qb1,Qc1)为数控机床加工刀心方位坐标。

计算数控机床刀轴正方向矢量:

(3)

式中:[Ja1,Jb1,Jc1]为数控机床加工刀轴方位矢量。

2)数控机床运动学逆解模型。

在已知数控机床刀心方位坐标(Qa1,Qb1,Qc1)和刀轴方位矢量[Ja1,Jb1,Jc1]情况下,计算数控机床进给轴的运动方位,表达式如下:

(4)

(5)

式中:θ为刀轴进给深度,Pa1、Pb1、Pc1表示a1、b1、c1的二维映射参数。公式(4)为数控机床运动学逆解模型。利用数控机床运动学正解模型和运动学逆解模型可计算得到数控机床刀心与刀轴的实际位置。

1.2 数控加工误差计算

1.2.1刀心位置轮廓误差计算

由数控机床运动学正解模型可知,零件在三维坐标系下,机床刀心位置水平方向的分量会同时受到3个移动轴a2、b2、c2和2个转动轴d2、e2影响[8],其垂直方向分量则受到a2、b2、c2轴影响。当a2轴移动角度为da2时,数控机床刀心位置变化量计算公式如下:

(6)

式中:dFa2、dFb2、dFc2分别为数控机床刀心位置坐标在3个移动轴的变化量,(Fa2,Fb2,Fc2)为数控机床刀心位置坐标。

当a2轴在传动过程中出现误差时,通过公式(6)即可计算其刀心位置变化量,同理利用公式(6)可计算其他两轴在传动过程中出现误差时机床刀心位置变化量。

将式(6)转换成矩阵形式:

(7)

将式(7)中的矩阵替换为数控机床移动轴的运行速度和时间的乘积,轴移动角度替换成角速度和时间的乘积,则数控机床刀心位置在不同方向上的速度变化量计算公式如下:

(8)

式中:Va2、Vb2、Vc2分别为数控机床在三维坐标系3个方向上的速度变化量,νX、νY、νZ分别为a2、b2、c23个移动轴的移动速度,ωA、ωC分别为d2、e22个转动轴的转动速度,t为时间。

由此即可得到数控机床刀轴位置和刀轴运动速度的误差。

1.2.2刀轴方向轮廓误差计算

由数控机床运动学逆解模型可知,刀轴轮廓误差受2个转动轴d2、e2影响较大,不受3个移动轴a2、b2、c2影响。利用数控机床运动学逆解模型,可得到数控机床刀轴方向轮廓误差,计算公式如下:

(9)

式中:dOa、dOb、dOc分别为数控机床刀轴在转动轴三维坐标系a、b、c3个方向上的误差,α和γ分别为转动轴d2、e2与刀心的夹角,dα和dγ分别为α和γ的误差。

经过上述计算,可得数控机床在运行过程中刀心与刀轴的误差。

1.2.3基于PID控制器的数控加工误差在位修正方法

利用数控机床运动学正解模型获得每个轴的实际位置后,将该实际位置值代入数控机床运动学逆解模型内,可得到轴交点A在刀具坐标系X、Y、Z中的实际坐标位置(HMX,A,HMY,A,HMZ,A):

(10)

式中:HX,A、HY,A、HZ,A、βA、γA分别表示轴交点A在数控机床轴d2、e2、a2、b2、c25个轴运动时的实际位置,L为轴交点到刀具坐标系原点的距离。

将刀轴轮廓误差代入数控机床的逆解模型中,利用该模型输出数控机床3个移动轴刀尖运行轮廓误差补偿点r的位置(HX,r、HY,r、HZ,r):

(11)

式中:PMX,r、PMY,r、PMZ,r、βr、γr是数控机床轮廓误差补偿点r在轴d2、e2、a2、b2、c25个轴运动时的实际位置。将公式(11)的计算结果减去公式(10)的计算结果,即可得到数控机床d2、e2、a2、b2、c25个轴在t时刻的对应位置误差补偿值Δx(t)、Δy(t)、Δz(t)、Δβ(t)、Δγ(t)。将数控机床每个轴的补偿值输入到PID控制器内,对数控机床轮廓加工在位误差进行补偿,最终得到的误差修正结果如下所示:

(12)

式中:Δxbc、Δybc、Δzbc、Δβbc、Δγbc为数控机床各轴的加工误差修正结果,i为机床加工次数,kp,x、kp,y、kp,z、kp,β、kp,γ为数控机床各轴比例系数,ki,y、ki,z、ki,β、ki,γ为数控机床各轴的加工次数积分系数,kd,x、kd,y、kd,z、kd,β、kd,γ为数控机床各轴的微分系数。利用式(12)即可实现复杂深孔内轮廓数控加工误差在位修正。

2 实验分析

以DHD1010-10R型深孔钻铣复合数控机床为实验对象,主轴可向上旋转15°,向下旋转25°,且配有数字显示转台,可适用于高精度深孔零件和斜孔零件的加工,该复合数控机床加工孔径范围为3～25 mm,加工深度为1 000 mm,轴最高转速为6 000 r/min,进给速度可达到3 000 mm/min。

2.1 刀尖运动位置测试

以该复合数控机床某移动轴为实验对象,使用本文方法计算该移动轴刀尖的纵坐标位置,结果如图1所示。

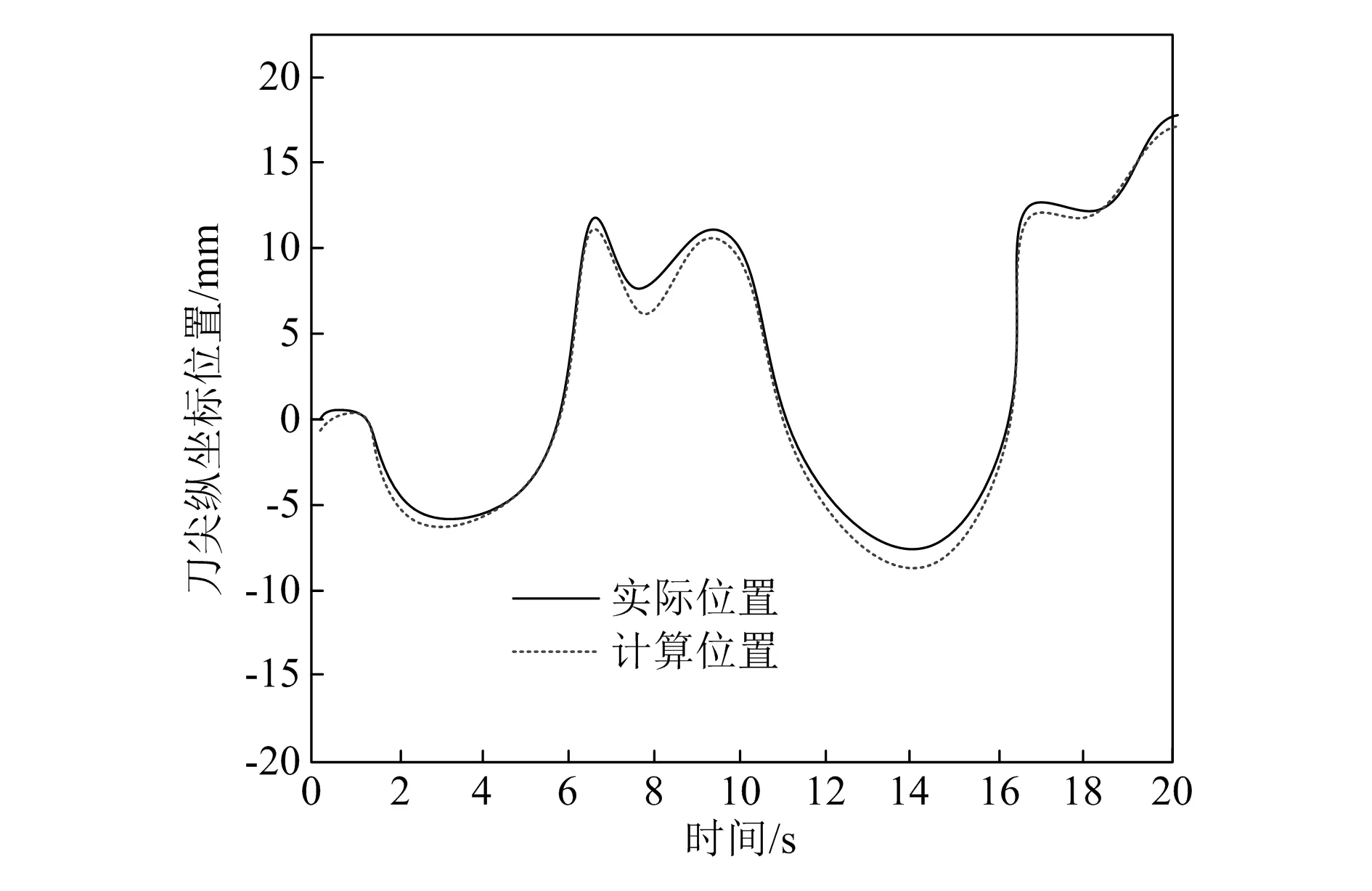
图1 移动轴刀尖纵坐标位置计算结果

分析图1可知,该复合数控机床移动轴刀尖的实际纵坐标位置随着时间的增加呈现不规则波动变化,而使用本文方法计算出的移动轴刀尖纵坐标位置曲线与实际位置曲线重合度极高,仅在8 s和14 s时,计算结果与实际结果存在1 mm左右的误差,该误差数值符合加工要求。由此说明应用本文方法计算出的数控机床加工移动轴刀尖位置坐标较为精准。

2.2 数控机床加工误差计算

以该复合数控机床其中一个转动轴作为实验对象,使用本文方法计算该转动轴旋转角度误差,计算结果如图2所示。

图2 复杂深孔钻铣复合数控机床转动轴旋转角度误差

分析图2可知,复合数控机床转动轴旋转角度误差在X轴和Y轴方向上数值均在0.07°以下,符合数控加工要求。由此可知,利用本文方法可准确计算该复合数控机床转动轴在X方向和Y方向上的误差,为修正数控机床加工误差奠定良好基础。

进一步验证本文方法计算数控机床加工误差效果,以误差作为衡量指标,测试本文方法的转动轴进给量误差计算效果,并设置误差计算结果的偏差阈值为0.010 mm。测试结果见表1。

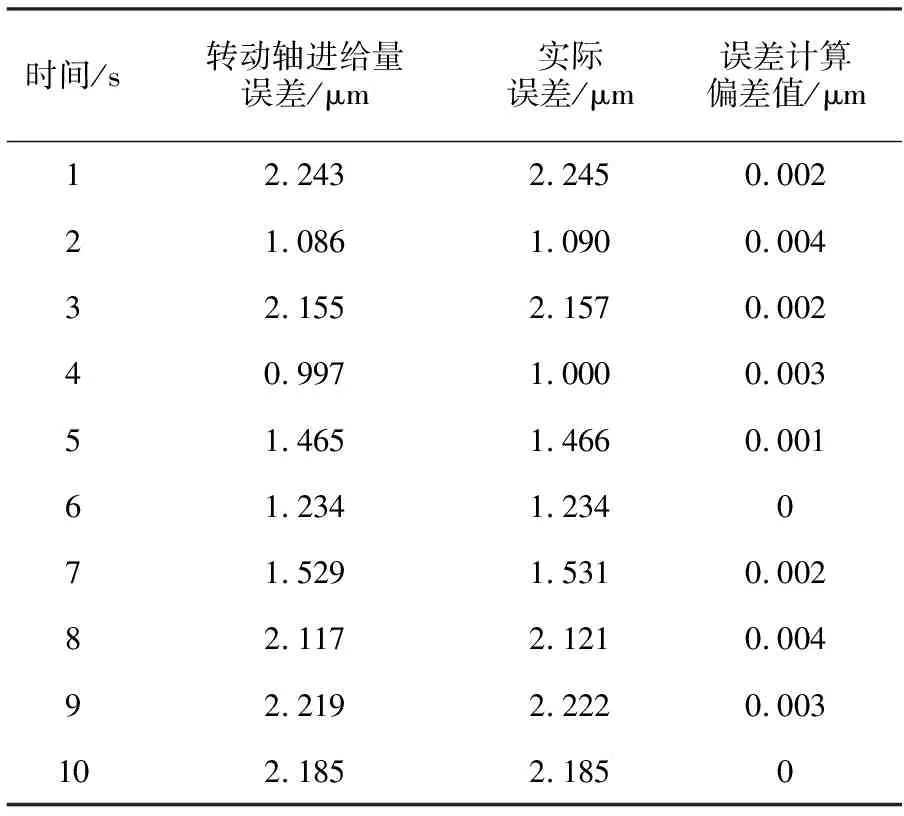
表1 数控机床转动轴进给量加工误差计算偏差值

分析表1可知,该数控机床在加工精密零件过程中,轴进给量误差呈现波动变化,但波动幅度较小。而本文方法计算出的该数控机床加工误差与实际误差的偏差值最小为0 mm,最大仅为0.004 mm,均低于预设的误差计算偏差阈值。上述结果表明:利用本文方法计算的数控机床加工误差小且精准。

2.3 数控加工误差在位修正测试

使用数控机床加工不同类型深孔零件,以刀心位置和刀轴轮廓作为研究对象,使用本文方法对该数控机床加工误差进行在位修正,修正效果如图3所示。

图3 数控机床加工误差在位修正效果

由图3可知,该数控机床在加工复杂深孔零件时,其刀轴轮廓加工位置存在误差,使用本文方法对该数控机床加工误差进行在位修正后,其刀轴轮廓位置误差明显减小,更接近目标位置。量化的修正结果见表2。

表2 数控机床加工误差在位修正结果

分析表2可知,该数控机床在加工不同类型复杂深孔零件时,其刀轴方向轮廓误差均高于刀心位置轮廓误差。使用本文方法对数控机床加工误差进行在位修正后,其刀心位置轮廓误差和刀轴方向轮廓误差均降低至0.005 μm以下。上述结果表明:本文方法可准确对数控机床加工误差进行在位修正,从而降低其轮廓加工误差。

以该数控机床加工不同类型复杂深孔零件时的淘汰率作为衡量指标,测试本文方法应用效果,测试结果如图4所示。

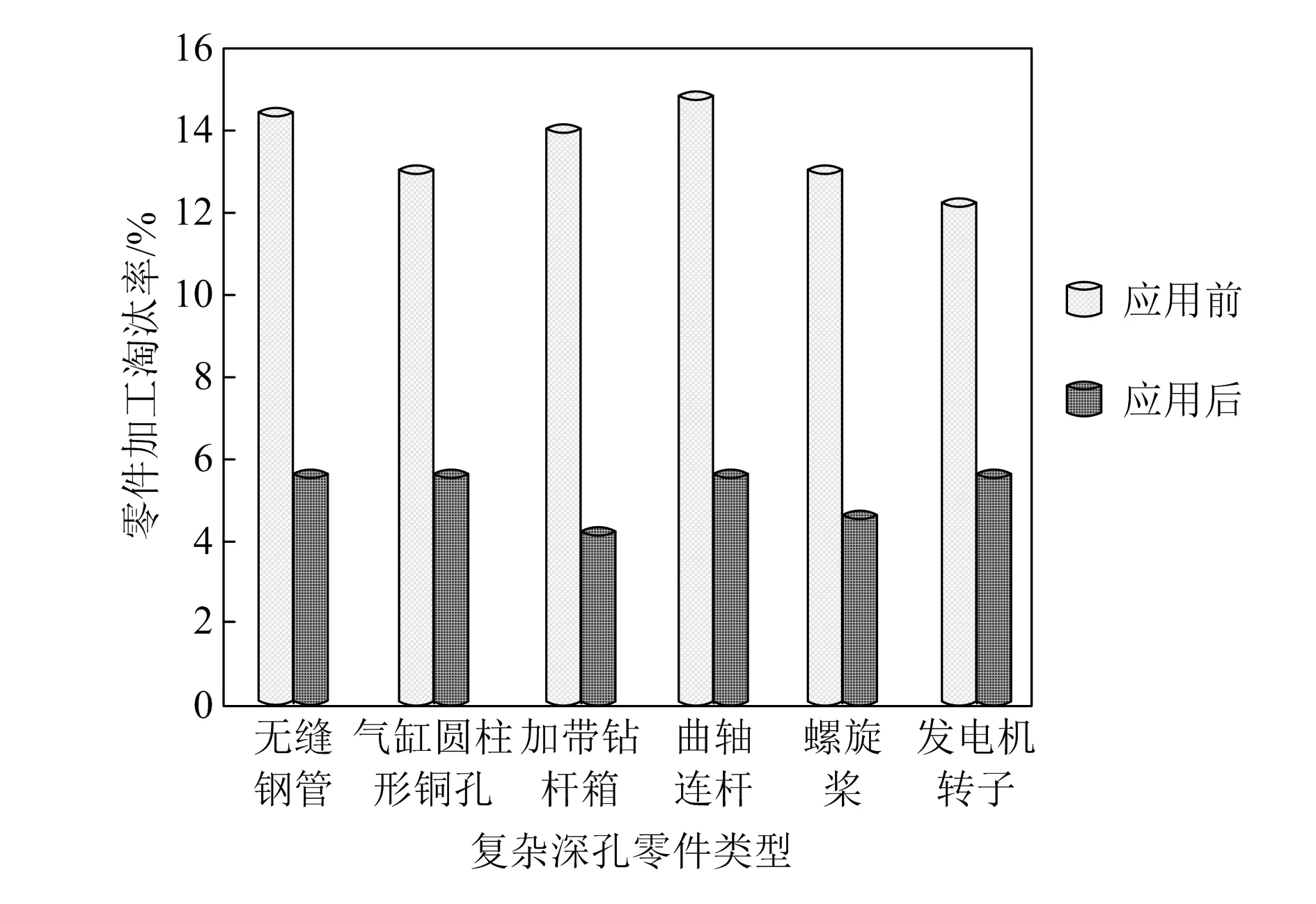
图4 复杂深孔零件加工淘汰率

分析图4可知,应用本文方法前,数控机床加工不同类型深孔零件时,其零件的淘汰率为13%～16%。应用本文方法后,零件的淘汰率降低至4%～6%。由此说明应用本文方法可有效降低数控机床加工零件的淘汰率,应用效果较佳。

3 结束语

加工复杂深孔零件的数控机床在应用时,受伺服系统影响,容易出现误差。为了降低加工误差,本文提出复杂深孔内轮廓数控加工误差在位修正技术。测试结果表明,该方法使刀心位置轮廓误差和刀轴方向轮廓加工误差均降低至0.005 μm以下,零件的加工淘汰率降低至6%以下。由此可见,该方法可有效修正复杂深孔内轮廓数控加工误差,从而有效提升复杂深孔内轮廓数控机床加工水平。