高中数学解题思路的有效引导探讨
张彩琴 王治伟
【摘要】文章以帮助高中生走出数学解题困境与误区为出发点,对高中数学解题思路的有效引导方式展开了深度探讨.首先,对常见的高中数学解题思路进行了梳理,其次,以结合湘教版高中数学教材经典例题的方式详细探讨了在具体数学问题解决中的有效解题思路引导策略,旨在通过对高中数学解题教学模式的完善优化,规避“题海战术”教学问题的持续蔓延,进一步驱动学生数学解题思维与解题能力的提升.
【关键词】高中数学;数学解题;解题思路;有效引导方法
数学解题是高中数学教学的重点与难点,对学生高阶思维能力以及数学综合素质有着较高的要求.这就使得思维能力正处于上升阶段的高中生在实际解决数学问题的过程中,往往会陷入思维误区之中无法自拔,这不仅会加剧学生对数学解题的厌学与排斥、抵触情绪,同时会使学生深度数学学习的实现与数学核心素养的发展受到消极影响.因此,在现如今的高中数学解题教学中,灵活运用多种数学思想方法与解题技巧培育学生数学解题思维,引领学生走出思维定式尤为关键.
一、常见数学解题思路梳理
确定正确的解题思路是实现高效解题、准确解题的关键.通过对高中数学课程教学内容的分析以及对前人研究思路的整合,笔者认为在高中数学解题教学中较为常用的解题思路主要有变形思路与代换思路两种.
第一,变形思路.顾名思义,是一种应用多种变形手段将复杂深奥、晦涩难懂的数学题目转化为易操作、易解决的简单问题,进而实现快速解题与准确解题的数学解题思路.具有代表性的数学解题方法有构造法与数形结合法.
第二,代换思路.是一种将两种相互关联的数量转化为一种数量,即用另外一种数量替代原有问题中的数量,进而更为迅速找到解题突破口的解题思路.具有代表性的数学解题方法有换元法与假设法.
除了以上两种常见数学解题思路外,可应用于高中数学问题解决的思路还有很多,在实际的高中数学解题教学中,教师需根据具体数学问题的类型与解决需要采取更为灵活有效的方法对学生进行针对性引导,以此来让学生的数学解题速度与准确性得到稳定提升.
二、高中数学解题思路的有效引导策略
高中数学问题具有题型多样、种类多元的特点.因此,若想让学生在实际解决与分析数学问题时,学会合理灵活地应用多种解题思路进行高效解题,高中数学教师就要以学生一般数学解题逻辑为线索,将行之有效的引导策略嵌入到学生的审题、析题以及解题过程之中,以此更好地促进学生良好数学解题习惯与思维的形成.
(一)变换视角,多角度审题
审题是学生展开数学解题活动的第一步,对解题思路的明确、解题方法的确定起决定性作用.因此,在高中数学解题教学中,教师就要重视起学生审题过程中解题思路的引导.不同于义务教育阶段,高中阶段的数学问题的综合性、逻辑性以及抽象性更强,并且包含了数学公式、函数方程、数学符号、几何图形等多元内容,这就使得学生在审题过程中往往会被题干中非必要条件、信息而干扰,无法“一针见血”地抓准解题的突破口.对此,高中数学教师在实际教学指导过程中,便可引导学生从“出题者”与“解题者”两个视角上进行审题,使其通过揣摩题目意图与考查内容的方式得到解题思路的清晰.
例如,在引导学生解决“一元二次不等式”一课的例题“解不等式-x2+4x-5>0”时,高中数学教师便可让学生从“出题者”与“解题者”两个视角进行审题,梳理题目中的已知条件、隐含条件以及求解目标,进而得到明晰的解题思路与明确的解题方法.
第一,从出题者视角审题.解不等式问题是“一元二次不等式”一课的重要内容,在此之前通过学习“相等关系与不等关系”“从函数观点看一元二次方程”等课程知识,学生已对一元二次不等式的原理概念形成了一定的了解认识.因此,例题“解不等式-x2+4x-5>0”的目的在于让学生掌握解决一元二次不等式的基本方法,学会借助二次函数图像的直观性完成解题,锻炼学生的数学解题能力,加深学生对数形结合思想方法的认识把握,驱使学生将一元二次不等式与二次函数建立起更深的联系.
第二,从解题者视角审题.根据已知数学知识可知,方程-x2+4x-5=0没有实根,所以,根据二次函数与一元二次方程之间的联系,可以确定二次函数y=-x2+4x-5的图像与x轴没有交点,即可得出不等式-x2+4x-5>0的解集是空集“?”.
综合以上两种审题视角,学生的数学解题思路会更清晰,回到本课例题的解决上,学生便会提出解题方法:
解法一:
通過计算方程-x2+4x-5=0的判别式,可得Δ<0,
∴方程-x2+4x-5=0没有实根,
∴二次函数y=-x2+4x-5的图像与x轴无交点,如图1,
∴不等式-x2+4x-5>0的解集为?.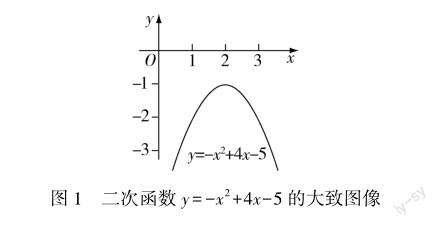
在此基础上,高中数学教师还可由解一元二次不等式的过程与方法出发,引导学生以表格的形式梳理一元二次不等式与其对应的一元二次方程、二次函数之间的关系,让学生通过对数学知识的梳理与整合,更好地认清数学知识之间所存在的逻辑关系,进而学会更加灵活地应对与处理高中数学一元二次不等式问题.
在审视阅读数学问题的过程中,引导学生从出题者与解题者两个视角上展开问题分析,不仅能够让学生更好地把握到解题的突破口,得到数学解题思维的发散活跃,还能让学生在灵活转化视角,合理揣摩分析数学问题意图的过程中,对数学问题中的已知条件、未知条件以及隐含条件也会形成较为全面的认识把握,从而提升学生数学解题效率与准确性.
(二)一题多解,深层次析题
高中数学问题具有较强的灵活性,且考查的知识内容并不限于某一知识点.因此,在学生解决数学问题时,常会出现“即便多角度审题也无法得到清晰数学解题思路”的情况,进而影响其数学解题的准确性与有效性.对此,高中数学教师在引导学生多角度审题,明确问题意图与求知目标后,鼓励学生灵活迁移运用已知的数学知识与解题技巧对数学问题展开深层次分析,并有意识地探究一个问题的多个解决方法,以此来更好地发散学生的数学解题思维,让学生经过深思熟虑找到更为有效的解题方法.
例如,在湘教版高中数学教材必修第二册“解三角形”一课教学中,引导学生解决以下问题时,高中数学教师便可运用问题导学法与小组合作学习法引领学生展开对数学问题的多元探究与深度分析.
【问题】分别求下列条件中△ABC的∠C与c.
其次,设置问题“解决这一问题中的两个小问,可以运用怎样的数学思想方法?”引发学生进行小组讨论与互动交流,让学生在“你一言我一语”的探讨中探索出不同的解题思路,并生成意见与想法的冲突.对此,高中数学教师便可见缝插针地设置导语让各个学习小组的学生根据个人的个性化见解与想法进行解题,而在学生纷纷完成数学解题后,高中数学教师则可让各个学习小组上台发言,讲述说明解题过程.
有的学习小组利用数形结合思想方法,根据已知题目条件与信息绘制了△ABC,并围绕具体图像完成了上述问题;有的学习小组则迁移运用平面向量知识,探寻出了不同的解题思路;有的学习小组利用转化思想将本题转化为了简单易操作的三角形内角和问题,虽未准确得出△ABC中c的准确数值,但也对本题的解决方法提出了更具创造性的见解.
最后,高中数学教师可向学生渗透解决这一问题的正确解法,让学生通过对照个人解题过程,并规范解题步骤,自主建立起正确的数学解题思路与解题思维习惯.
教師在学生分析数学问题的过程中,合理运用小组合作学习模式与问题导学方法引导学生展开对某一问题的多元探讨与深层次分析,不仅能够让学生的数学解题思维更加灵活敏捷,还能让学生在主动围绕个人个性化的解题见解与方法展开合理解题,数学解题思路也会因此而明晰.
(三)活用方法,高效率解题
高中数学问题的难度与复杂程度相较于初中数学问题更甚.因此,为让高中生的数学解题效率与质量得到更为坚实的保障,高中数学教师除要重视起对学生审题、析题的引导外,还要将多种数学思想方法融入学生的自主解题过程之中,以此来让学生在数学思想方法的加持下学会化难为易、化繁为简,得到数学核心素养的发展提升.

结 语
总而言之,在核心素养下的高中数学教学中,教师若想让学生实现从浅层数学学习到深度数学学习的良好过渡,在数学解题教学中帮助学生建立起正确的数学解题思路、养成良好的数学解题习惯至关重要.对此,高中数学教师在实际的数学解题教学中,可根据具体数学问题的特点与考查内容将多元灵活的解题方法、解题技巧合理嵌入学生的数学解题过程之中,以此为学生的数学解题提供灵感与启发,让学生通过多角度思考、多层面分析获得“拨云见日”之感,进而使学生在深刻领会数学解题乐趣与魅力的过程中得到数学学习水平的稳步提升.
【参考文献】
[1]庄素慧.基于“构造法”的高中数学解题思路探索[J].数理化解题研究,2022(31):55-57.
[2]刘剑华.高中数学解题思路以及解题能力训练方法研究[J].数理天地(高中版),2022(21):70-72.
[3]谢波.高中数学函数的多元化解题思路[J].数理天地(高中版),2022(15):66-68.
[4]鲁亚萍.核心素养下高中数学不等式的解题思路研究[J].中学课程辅导,2022(17):9-11.
[5]金家庆.探究高中数学解题思路以及解题能力的训练[J].数理化解题研究,2022(12):50-52.
[6]张玉杰.高中数学解题教学中分类讨论思想的培养思路浅述[J].求知导刊,2020(01):52-53.

