几何证明题解题思路研究
魏迎萍
【摘要】基础教育数学课程改革中,几何学作为数学的重要组成部分,成为人们备受关注的问题之一.文章主要是以近五年成都市中考试卷几何证明题为例,结合学生目前对于几何证明所遇到的问题,就几何证明题的解题思路进行研究.回看近五年来成都市中考试卷,其中平面几何每年都会以选择、填空、解答或证明题形式出现,题型灵活多变.文章归纳总结了几何证明题的一般解题思路和解题技巧,将“理论用于实践”,从未知到已知,进一步提升学生解决几何证明题的能力.
【关键词】平面几何;几何证明题;解题思路;成都市中考试题
引 言
一直以来,几何学作为中学数学的重要部分,在课程改革中,几何学的改革早已成为人们非常关注的问题.几何证明题难度较大,很多学生会因为“节约时间”“合理利用时间”等原因在未认真阅读题目的情况下放弃该题目,因此几何证明题也就成为拉开学生差距的题目.但几何证明题并不是非常高深的题型,如果学生能够掌握正确的解题思路,使用行之有效的解题技巧,不仅可以降低几何证明题的难度,也能够提高几何证明题的準确率.此外,学生对自己能够解决几何证明题的信心不足,也容易产生放弃的念头,如果教师在讲解几何证明题时能帮助学生整理解题思路,归纳解题技巧,长而久之,学生的解题能力自然会得到提升.下面笔者以成都市近五年中考真题为例,对几何证明题解题思路进行梳理.
一、读已知信息,从题目中提取有效信息
想要解几何证明题,审题非常重要.很多学生在拿到题目以后,没有标记的习惯,也没有分析所给已知信息的目的,这样不仅可能会导致审题错误,而且可能会导致无效审题.因此,学生在拿到一道题目后,首先要做的就是根据已知信息尽可能多地推测出与其相关的知识点.
例如,题目中给出“Rt△ABC绕某点旋转得到△A′B′C′”,学生便可以推测出:△ABC≌△A′B′C′,△ABC中有一角等于90°等信息,同时要考虑到初中所学过的所有与三角形有关的知识,如全等、相似、三角形外角和定理、中位线、等腰三角形的三线合一等,这些都是常考的知识点.
因此,有效读题,并不仅是读题目中的已知信息,而是要尽量根据已知信息,快速推测出相关知识点.
二、读题干,从题干中获取有效信息
题干中的信息是学生最容易忽略的地方,很多学生在阅读题目时更在乎需要解决的问题.而很多难度比较大的题目,关键条件都隐藏在题干之中,需要结合已知信息进行延伸,找到解题思路.学会引申最有效的方法就是学生平时多多积累,需要对定理、知识点非常熟悉.对于特殊的图形,学生在平时要记忆,在读题干、审题时也一定要加以标注,要做到从隐藏条件中提取相关知识点.在图形中进行标注,不仅可以帮助学生区分已知和未知信息,也可以帮助学生进一步思考,获取有效信息.
总之,读题时要做到以下几点,其一,细心读题,不要被陷阱给迷惑;其二,读题时要标记和记忆;其三,读题时要注意深度思考,很多信息不是题干直接给出的.
下面以成都市中考真题进行说明:
例1 (成都市2021年中考A卷第20题)如图1,AB为☉O的直径,C为☉O上的一点,连接AC,BC,D为AB延长线上的一点,连接CD,且∠BCD=∠A.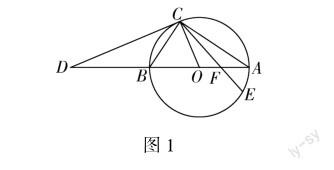
(1)求证:CD是☉O的切线;
(2)若☉O的半径为5,△ABC的面积为25,求CD的长;
几何证明题中的任何一个已知信息都不是孤立的.把握基本图形的组合,掌握知识点间的常见联系,积累解题经验是很重要的.
三、合理利用辅助线,降低题目难度
作辅助线是解决近五年来成都市数学中考试卷B卷几何证明题必不可少的一步,也是学生在解几何证明题时最难的一步.几何证明题常常涉及比较复杂的图形,但其实再复杂的图形,也是用常见的基本图形通过一定的组合得到的.基本图形的定义、公理、定理和推论是我们必须熟悉和掌握的内容,另外还有一些常见组合形式:如角平分线形、八字形、双垂直图形等.
在近五年成都市中考试卷中的几何证明题中,所做的辅助线主要有两种类型,即作某直线的平行线或者垂线.在作平行线时,会涉及平行线的性质,再利用与平行线相关的性质去证明某些图形的相似或者是三角形的全等,从而解决线段之间的关系;在作垂线时,会涉及三线合一或者与角度有关的知识,从而证明线段之间的关系.能否正确作出辅助线,实际上也在于平时的积累,教师在教授几何相关的知识时,可以侧重于使学生感受辅助线的自然生成.
在几何证明题中,辅助线的添加也具有一定的规律.在三角形中,遇到中点,添加中位线或中线;遇到角平分线,过角平分线上的点,添线构造全等三角形;遇到中线,延长中线至原长的二倍,构造全等三角形;截长补短构造等长直线等;添加平行线构造全等或相似三角形.在梯形中,作平行线,构造平行四边形;连接对角线,构造三角形;作垂线,构造直角三角形或矩形;遇到中点,作中位线或构造全等三角形.在平行四边形中,有平行线构造平行四边形;有中点构造全等三角形;过交点作垂线;有垂线时,构造矩形或作平行线.
四、理出思路,正确运用数学几何语言
数学学科具有精准性和严谨性,数学语言的合理利用是数学中考着重考查的部分,学生正式接触数学语言便是从几何开始的.教师在教授数学语言时,应促使学生养成正确运用数学语言的习惯.数学语言的正确表达,有助于学生形成数学思维.几何语言有连接实验几何和论证几何的桥梁作用,教师通过对几何语言例题的示范和训练来加强学生对几何知识的使用,真正意义上提升学生运用几何知识的能力,能够帮助学生理解复杂晦涩的数学知识,帮助学生进行清晰、有条理的思考,从而引导学生合理、正确地解决数学问题,加强对数学学习的认识,不断激发学生的思维能力.
五、回顾检查,是否有不符题意信息
回顾检查是解题的最后一步,也是较为重要的一步,但是很多学生在完成几何证明题以后,并没有检查的习惯,认为只要思路正确,便不会出错.事实恰恰相反.在几何证明题中,学生经常出现看错题目所给角度、所给直线,导致在理解错误的基础上反复解题,却一直没有收获,不仅浪费时间,而且影响做题进度、解题思路.因此,学生在解题的过程中,没有思路时,也应该注意回顾,检查是否有漏读、错读的信息.在近五年成都市中考数学试卷中,关于几何证明题,如果题目中没有涉及动点问题,所给出的图形一般来说是比较标准的.例如,学生可以根据对比已知直线的长度和所求解出来的直线的长度,判断最终结果是否符合题意信息.
六、解题思路的应用
下面以成都市2020年A卷第20题为例,对解题思路的五个步骤进行应用.
(3)若F是AB的中点,试探究BD+CE与AF的数量关系并说明理由.
解题思路 根据上述所提供的的解题思路步骤,我们在拿到这道题后,先阅读题干的已知信息,整理有效信息,并且在已知信息的基础上,结合图形,引申出相关知识点,推测所给已知信息的目的.从题干中我们可以知道,所给的已知信息有:OC是☉O的半径、☉O与AB相切于点D、AC=AD,同時,我们可以利用已知信息结合图形推测出OC=OE、∠ODA=90°.第二步是读问题,前文已经提到,几何证明中,如题目是要求证明某一知识,我们可以直接将该问题看做已知,进行逆向思考.若AC就是☉O的切线,那么过C点的半径一定是和AC垂直的,结合上段所提取的信息,可以推测出∠ODA=∠OCA,进行到此时时,便可以看出△AOC≌△AOD,利用SSS定理便可以轻易得证.整理思路以后,再利用几何数学语言将解题过程表达出来即可.

第三小问中给出了一个新的信息,F是AB的中点,要求探究BD+CE与AF的关系,这三条线段初看似乎没有任何联系,因此我们要结合已知信息进行分析,OC是☉O的半径,☉O与AB相切于点D,AC=AC,F是AB的中点,将信息尽量套到同一个图形之中.当我们在图中标注了这三条直线以后,会发现,由于F是AB的中点,且B,D,A三点在同一条直线上,此时最主要的就是解决CE和这两条线段的联系.连接ED,我们可以观察到,ED和FD之间似乎是相等的关系,如果可以证明他们两者相等,便把题目中一开始看似毫无关联的三条线段,放在了同一条直线AB上,题目也就得到了解决.
结 语
总之,对学生几何证明的思路及思维进行训练,有利于培养学生数学逻辑能力以及核心素养.几何证明虽然是初中生普遍认为的难点,但是也仍然有可以破解的方法.作为教师,在教授几何相关知识时,要注意有意识地培养学生的数感,在平时训练时要重视实践.实践是初中数学证明的基本出发点,贯穿于证明教学的全过程.同时,教师应该注意及时对学生进行纠错,特别是数学几何语言,促使学生养成好的数学习惯,端正对于几何证明题的学习态度.
【参考文献】
[1]秦晓.例谈初中几何证明中“辅助线的自然生成”[J].数学教学通讯,2019(11):42-44.
[2]林丽红.初中几何证明题解题技巧探析[J].中国培训,2015(10):214.
[3]李淑琴.初中数学证明题解题方法探讨[J].当代教研论丛,2015(09):53.
[4]钟万明.浅谈平面几何证明中信息的处理[J].数学学习与研究,2013(12):94.
[5]高长红.几何证明添加辅助线的技巧[J].科学大众(科学教育),2011(09):28.
[6]王锡珠.初中数学几何图形语言的训练策略[J].理科考试研究,2016,23(02):4.

