液滴在运动超疏水表面回弹特性的研究

霍本洁,钱丽娟,2

(1.中国计量大学 机电工程学院,浙江 杭州 310018;2.浙江省智能制造质量大数据朔源与应用重点实验室,浙江 杭州 310018)

液滴撞击固体表面是一种广泛存在的现象,在自然界和日常生活中随处可见,如在飞机飞行过程中[1-2]、风力涡轮机运作[3]、喷雾冷却[4]、化学涂层[5]等,学者们对此做了很多研究,但大多集中在静止表面,对液滴撞击运动表面的研究较少。而液滴撞击运动表面在自清洁、防结冰和液滴控制等领域具有实际应用,因此研究液滴在运动超疏水表面的回弹有重要意义。

最大铺展直径和接触时间是衡量表面特性的重要参数。Mao等[6]研究了在室温下液滴撞击固体表面的铺展和反弹实验,发现影响液滴最大铺展直径的主要因素是液滴的撞击速度和粘度,影响液滴反弹的主要因素是液滴的粘度和静态接触角。Clanet等[7]发现液滴在超疏水表面的最大铺展直径与韦伯数We呈幂函数关系。Srivastava等[8]为解释液膜外围形成的边缘,重新计算了液滴在最大铺展状态时的表面能,并通过能量守恒公式建立了预测液滴最大铺展直径的模型。Almohammadi等[9]通过实验推导出液滴在平动表面上呈非对称扩散的模型。Zhan等[10]发现液滴撞壁过程中,液体和运动平面之间存在一薄薄的空气层,由于存在粘滞力、毛细力与惯性力竞争,导致液滴不对称延伸。无量纲最大铺展直径可由韦伯数和毛细数决定。

接触时间是液滴开始接触表面到液滴刚刚离开表面的时间。在防结冰等领域中,液滴不应与表面长时间接触,因此学者们使用了很多方法来减少接触时间。Liu在研究液滴撞击锥状微结构超疏水表面时首次发现了饼状回弹现象,水滴在铺展后,以扁平的煎饼形状离开表面,与传统完全回弹现象相比,饼状回弹的接触时间减少了四分之一[11-12]。Bird[13]在超疏水表面设计了一个宏观脊结构,液膜在收缩时产生非均匀速度场,实验表明液滴撞壁后的接触时间减少了37%。Chantelot等[14]在超疏水表面设计了一个突起后,发现液膜从边缘和中心同时收缩并发生环状弹跳,由于液滴收缩时间减少因此接触时间也随之减小。Zhang等[15]对比研究了液滴对平动和静止超疏水表面的冲击动力学。发现与静止超疏水表面相比,在移动超疏水表面上,液滴接触时间减少。Zhan等[10]认为液滴撞击超疏水表面时,表面速度越大接触时间越少。

前人对液滴撞击固体表面的最大铺展直径和接触时间做了充足的研究,但对液滴撞击运动超疏水表面的研究较少,研究并不充分。本文讨论了液滴撞击运动超疏水表面时表面速度与最大铺展直径的函数关系,进一步分析了收缩时间减小的原因,最后通过速度恢复系数分析了液滴的能量变化。

1 实验方法

1.1 实验装置示意图

图1显示了液滴撞击移动超疏水表面的实验装置,包括液滴发生器、线性滑动平台模块和图像捕捉系统。液滴发生器由一个微型注射器泵(LSP02-1B)、一个注射器和一个可升降台组成。微型注射器泵以恒定的速度推动注射器,可稳定产生大小均匀液滴,并撞击目标基板。法线撞击速度Vn随着液滴滴落高度的改变而发生变化。线性滑动模块由伺服电机、伺服控制器和线性导轨(无锡迪恩斯传动技术有限公司,HS80-TBD-SF60-500)组成,导轨上的基质以特定速度Vs(0.1～1.5 m/s)移动。图像采集系统包括一个高速摄像机(Fastcam Mini AX 100-C),一个显微镜镜头(Raynox DCR-250),和一个无频闪LED聚光灯,以捕捉液滴撞击超疏水表面的快照。

图1 实验装置示意图Figure 1 A schematic diagram of the experimental setup

1.2 表面的制备和表征

超疏水表面由紫铜基板加工而成,基板尺寸为20 mm×100 mm×3 mm。将基板依次放在丙酮、无水乙醇、盐酸中进行超声波清洗和除锈,最后用蒸馏水和无水乙醇再次清洗。然后将纳米超级干涂料(NC319 NeverWet, Ultra every dry)喷涂在基板上,在20～25 ℃的室温下放置2 h晾干基板,重复喷涂和静置操作3次完成超疏水表面的制备。用接触角测量仪(承德鼎盛试验机检测设备有限公司的JY-82C)测量水滴在表面的接触角,静态接触角θe=152°,滚动角θG=8°,接触角和表面形貌如图2。

图2 超疏水表面的静态接触角与形貌图像Figure 2 The static contact angle and morphology images of superhydrophobic surfaces

1.3 实验方法

2 结果与讨论

2.1 液滴撞击运动超疏水表面的实验现象

如图3(a)所示为液滴撞击静止超疏水表面的实验图,图3(b)显示了液滴以0.63 m/s速度撞击移动速度为0.75 m/s超疏水表面上的铺展和收缩过程。图3(c)展示了液滴离开表面后在空中的运动形态,红色箭头为表面的运动方向,且该图中液滴实验工况与图3(b)一致。如图3(b),液滴撞击运动超疏水表面时,切向动量的存在使液滴在撞击时受到壁面剪力的作用,使接触线在沿表面的运动方向上铺展得更为迅速。当液滴在接触表面后,上层液体仍然是球状,下层液体在表面剪切力的作用下层层铺展,液滴在达到最大铺展时液滴轮廓呈现由半圆和半椭圆组成的几何结构。在回缩阶段(t*=0.82后,回弹前),液滴的回缩是不对称的,运动表面带动下游液滴运动,而在惯性力和表面张力的作用下液体往上层移动,使得上游液体体积较大,而下游体积较小如图4。如图3(c),液滴在回弹后,液滴在空中振荡并沿表面运动方向移动,最后落回表面,振荡过程中液滴是不对称的,振荡也不在竖直和水平方向上,而是以倾斜的角度振荡,这是因为液滴从运动表面回弹时液滴就是倾斜的,由不对称的表面张力所导致。前人的研究也报道了撞击液滴的不对称铺展和收缩行为,不仅在移动的亲水表面[16]和疏水平面上[17]存在,而且在倾斜[18]、弯曲表面[19]或宏观纹理表面上[20]均存在这一现象。但是不对称行为导致的接触时间的缩短只发生在超疏水平面上[21-22],同时对液滴撞击运动超疏水表面接触线的长度和速度恢复系数的研究较少。因此在下文讨论了液滴撞击运动超疏水表面的最大铺展直径和速度恢复系数。

图3 液滴撞击壁面的形态变换Figure 3 The morphological transformation of droplets impacting the wall

图4 液滴接触运动超疏水表面的示意图Figure 4 Schematic diagram of a droplet contacting a moving superhydrophobic surface

2.2 铺展

液滴在运动超疏水表面上的铺展由于受到表面剪切力的作用而呈现非对称铺展,沿着表面运动方向的接触线变长,而垂直表面运动方向的接触线长度不变,Zhan等[10]和Zhang等[15]发现液滴在垂直于表面运动方向上的最大铺展直径与静止表面基本一致,不随表面速度的变化而变化。液滴沿着表面运动方向的接触线长度由两个因素决定:液滴的初始动能,液滴的初始动能越大,液滴的铺展直径越大;表面的运动速度即表面对液滴的剪切力,表面剪切力的存在使液滴在沿表面运动方向上层层铺展。表面剪切力来源于表面对液滴的粘附力,当液滴撞击表面时,液滴与表面间的固液接触部分,液滴会与表面发生一定的粘附,这种粘附作用在表面运动时可以拉伸液滴,使液滴的最大铺展直径增大。我们观察到在铺展阶段,液滴的顶点在水平方向是静止的,不会随着基板的运动而运动,如图5中虚线表示液滴顶点的位置。表面剪切力只影响与表面直接接触的下层液体,而上层液体不会随着基板的运动而运动[9]。

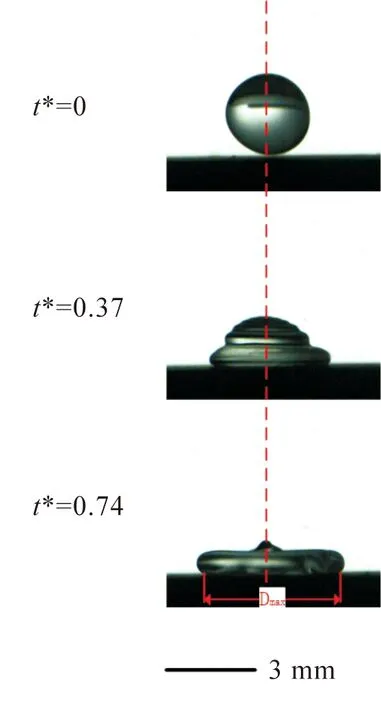
图5 液滴的铺展过程图Figure 5 Experimental diagram of deoplet spreading

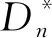
图6 D*随Vs和Wen的函数变化图Figure 6 Variation of the D* as a function of Vsand Wen

(1)

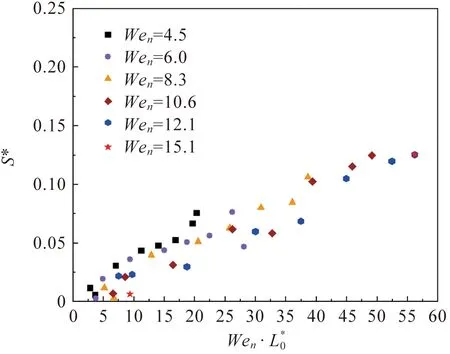
图7 拉伸长度S*与Wen的关系Figure 7 Variation of the tensile length S* as a function of Wen

(2)

(3)

则拉伸长度S*,可表示为

(4)

将式(4)代入式(1),可以得到以下修正后的下落撞击的无量纲最大铺展直径表达式:

(5)

将Vs=0.1～0.7 m/s的实验数据进行回归拟合,确定适合本实验的标度因子c=0.000 08。为了保证c的可靠性,使用Vs=0.75 m/s的实验数据进行验证,如图8中的数据点所示,数据点为模型预测值除以实验测量值,可以看出模型与实验数据较为吻合。切向最大铺展直径可表示为

图8 D*的实测值与预测值的比较Figure 8 Comparison between the measured and predicted values of D*

(6)

2.3 接触时间

图9显示了在不同Wen下,无量纲接触时间t*随表面运动速度Vs的变化关系,可以发现接触时间均在2.5左右附近,t*与Wen无关[26],但t*随Vs的增加而略微减少[27],这说明接触时间主要受表面移动速度的影响。为进一步阐明表面速度Vs对接触时间t*作用,将其分解为铺展时间τs和回缩时间τr。如图10,可以发现铺展时间数值大致相同,收缩时间随着表面速度的增加而缩短,这表明接触时间缩短的主要原因是收缩时间减小,也就是说,液滴铺展后收缩速度变快了。从图11中Wen=15.1,Wes=21.7的右侧曲线斜率较大,也可以看出表面速度越大,液滴收缩得越快。Zhang等[15]得出收缩时间的模型为τr=τr0(dx/dy)1/2,dx和dy分别是垂直于表面运动方向的铺展直径和平行于运动方向的铺展直径,τr0是液滴撞击静止表面的收缩时间。他们认为该模型与实验的偏差来源于收缩速度不恒定,事实上该模型忽略了下游液体的影响,而假定只有上游液体收缩。因此本文认为计算误差来自下游液体,下游液滴受到表面对其的影响而导致上游液体收缩速度增加。因此由于液膜厚度减小以及在下游液体的作用下,使得液滴的回缩时间减小。

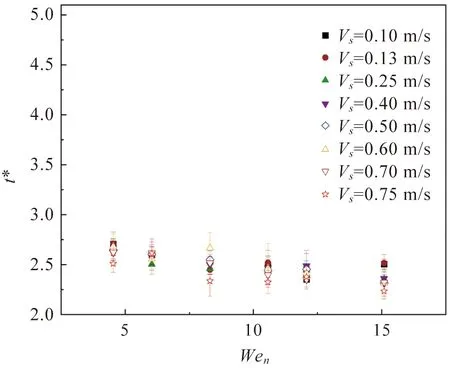
图9 t*与Wen的函数变化图Figure 9 Variation of the normalized contact time t* as a function of Wen

图10 铺展时间τs和收缩时间τr随Wen的变化Figure 10 Variation of the spreading time τs(hollow dots) and retraction time τr(solid dots) with Wen

图11 平行于表面运动方向上的铺展长度随时间的变化Figure 11 Spreading length over time in the directions parallel to the surface motion

2.4 速度恢复系数

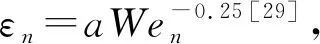
图12 不同表面速度Vs下Wen对εn的影响Figure 12 εnversus Wen at several different surface velocities Vs

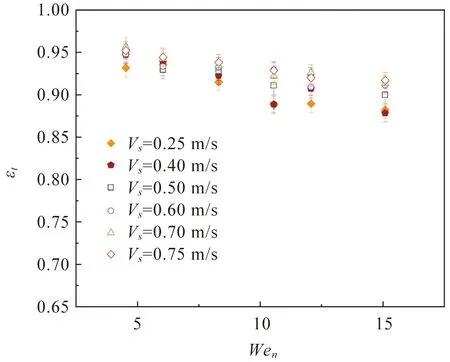
图13 不同的表面速度Vs下εt与Wen的关系Figure 13 εtversus Wen at several different surface velocities Vs

3 结 语

本文讨论了液滴撞击运动超疏水表面时,超疏水表面的运动速度Vs和法向韦伯数Wen对最大铺展、接触时间和速度恢复系数的影响,并分析液滴回弹的机理,得到了相关经验公式,具体结果如下。

液滴撞击超疏水运动表面过程中,液滴达到最大铺展时呈现为半圆和半椭圆组成的几何结构。无量纲最大铺展直径D*受两个因素决定:液滴的初始动能和从基板转移到固液接触下层液体的动能,后者沿表面运动方向拉伸液滴,使液滴层层铺展。液滴沿表面速度方向的铺展受剪切力的影响,拉伸长度与液滴的撞击速度和表面速度有关。表面运动速度越大,接触时间越小。收缩时间减小导致接触时间减小,而铺展时间不受表面运动速度的影响。液膜变薄和下游液体的作用使收缩速度增加,缩短了收缩时间。