基于标准距离端点数据重组的标定优化方法

陈雨婷,谢胜龙,邹 伟

(1.中国计量大学 机电工程学院,浙江 杭州 310018;2.中国计量科学研究院,北京 100029)

近年来大尺寸空间测量技术的应用日益广泛,随着测量任务难度增加,工业生产装备过程及现场在线校准对测量仪器的功能与实用性要求越来越高[1-2]。对于目标空间位置和运动轨迹的测量,目前应用较多是多边法。多边法由多台仪器联合同时测量目标,测量前须标定仪器参数,再由标定过的系统参数参与测量,因此,保证系统参数标定精度对后续测量是尤为重要的[3]。

国内外学者对系统参数标定方法的研究现状如下。Majarena等[4]使用三坐标测量机测量并联机构自身安装的球体,以获取并联机构在不同位置时球体的参考空间坐标,将参考坐标值进行坐标系转换后再对并联机构进行标定;Aguado等[5]将三台激光跟踪仪布置在数控机床周围做径向和纵向测量,通过跟踪数控机床的刀具获取空间中多点的位置信息[6],对比刀具移动距离和激光跟踪仪测量距离,利用最小二乘平差法对仪器位置进行二次校准标定;Conte等[7]为标定单台激光跟踪仪,采用多站位法测量三坐标测量机测量的标准长度,建立了对比误差最小化的测量模型,减少了测量点数;Sun等[8]在标定星跟踪器时通过改变相机位置,从多角度测量目标,二次测量保证了模型标定精度;Wan等[9]利用一台激光跟踪仪通过多站法,测量多组空间点位置,建立了基于不同测量误差沿三个坐标轴分布的加权模型,得到模型中协方差最小的最优仪器参数;林永兵等[10]针对四路激光跟踪干涉测量系统提出一种无约束动点自标定的方法,建立了空间点与仪器之间的距离模型,将残差二次方作为评价方法,测量多个空间点直至点数满足系统参数标定条件,操作简单;缪东晶等[11]提出一种七路激光跟踪干涉位姿测量系统的标定方法,通过将被测平面的三点极其间距包含到标定过程中,实现同时标定系统参数和静态位姿的测量;郑继辉等[12]在无约束动点自标定的基础上加入了加权标准长度约束,使用激光跟踪仪的干涉模式配合平面反射镜测量若干长度作为参考,再使用标准长度进行标定。多边测量系统的标定方法按照仪器位置分为单台仪器多站位二次标定和多台仪器同时进行标定,多台仪器的标定方法基本以参考物作标准[13-16]。

多边测量系统以激光跟踪干涉仪为例,使用四台及以上测量目标空间位置,六台及以上实现位姿测量,测量与标定均遵循干涉测距原理。标定时加入若干固定点组成的标准距离作为约束,靶球放置于标准距离两端靶座获取固定点对应的干涉测长值,由于干涉测距误差存在,引起标准距离标定误差增加,导致系统参数的标定误差增加。若多次标定则标定数据冗余且效率较低。为提高标定效率减小标定误差,本文在标准距离约束标定的基础上,提出一种固定点标定数据重组的标定优化方法,通过增加标准距离固定端点的标定测长获取次数,在不改变标定点顺序的前提下将固定点的对应测长重新组合扩大标定数据组数,迭代筛选得到标定最优组合,从而减小标定误差,进一步降低了系统测量误差。

1 系统参数标定方法

1.1 标定布局

本文采用六路激光跟踪干涉仪进行标定和测量。六台激光跟踪干涉仪Sn(n=1,2,3…6)的布局关系为:S1作为坐标系原点(0,0,0),S2位于x轴上设为(xS2,0,0),S3位于xoy平面内设为(xS3,yS3,0),S4、S5、S6靠近xoy平面坐标依次为(xS4,yS4,zS4)、(xS5,yS5,zS5)、(xS6,yS6,zS6)。在空间内设置6个固定点(P1～P6)组成4段标准距离di(i=1,2,3,4),标准距离由文献[12]中激光跟踪仪的干涉模式和平面反射镜结合的方法测量得到。在x方向3个不同高度各选取均匀分布的10个点,共36个空间点Pk(k=1,2…36),P7～P36为无距离约束的随机空间点。

初始点P1为基站获取初始测长的固定点,标定后系统进行测量时仍需在该点获取初始测长,将初始点作为两段不同方向的初始距离的共同端点,标定时采用两段标准距离约束该点的空间坐标,如图1。

图1 六路激光跟踪干涉仪标定布局Figure 1 Calibration layout of six laser tracking interferometer

1.2 标准距离约束算法

6台激光跟踪干涉仪的待求参数为12个,每台基站在初始点对应的初始距离设为ln0,待标定的参数共18个,激光跟踪干涉仪跟踪靶球在任一空间点获取的激光跟踪干涉仪测长为lnk空间点相对于初始点P1的长度变化量为

Δlnk=lnk-ln1。

(1)

每个空间点与基站的相对距离表示为

qnk=ln0+lnk。

(2)

因此通过基站表示空间点的坐标如式(3):

(3)

将每个空间点对应的标定测长作为约束条件,基站与各点之间的距离应接近于测长表示的相对距离,通过两点间距离公式,以最小二乘法的思路构建基站与标定点间的空间位置关系,如公式(4):

(4)

加入4个标准距离的约束,约束的两固定端点间距离应与标准长度值接近,通过约束对应的固定端点间距获取固定点坐标,由此构建固定点距离约束方程(5):

(5)

其中wi为各距离约束的权重值,将式(3)中的Pk(xk,yk,zk)表达式代入式(4),当k=1～6时,Pk对应标准距离约束的固定端点,将式(3)的Pk表达式代入式(5),构建方程为超定方程,设定求解参数的初值,采用Levenberg-Marquardt法进行迭代求解。

1.3 标定优化方法

用于系统参数标定的空间点分为固定点与非固定的随机点,对于固定点而言,除距离约束外也受基站干涉测长约束。将每个标准距离固定端点的干涉测长采集次数由1增加到h,每个固定端点有h个集合,每个集合中包含6个干涉测长元素,按照标定空间点顺序,对所有固定端点的集合进行重新组合。初始点P1对应的Δlnk为0,故实际重组的是5个固定端点的标定数据,标定组数由h变为M:

(6)

每组包含的标定点数依然为36个,对重组后的每一组数据依次代入算法进行迭代筛选,流程如图2。

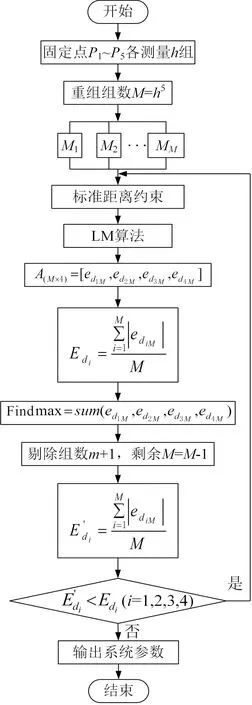
图2 优化算法流程图Figure 2 Optimize algorithm process

通过LM法进行非线性最小二乘求解系统参数,标定的标准长度端点为Pd,1,Pd,2,计算所有组的标准长度误差绝对值的均值Edi,如式(7):

(7)

将Edi作为迭代优化的终止条件,搜索所有组中标定误差和最大一组并剔除,即依次剔除掉固定点对应干涉测长误差最大的组:

(8)

2 仿真实验

本文使用MATLAB对优化方法的标定效果进行仿真,设置如图1布局所示的空间点。标定空间为5 m×2 m×2 m的立方体,在标定空间中布置点P1(-1 300,2 000,4 000)、P2(-1 500,0,4 000)、P3(-500,0,4 000),P4(-1 500,4 500,4 000)、P5(-1 300,2 100,6 000)、P6(-1 300,3 000,6 000)作为固定端点,生成对应的标准距离参考值,并按照1.1节中的布局加入30个均匀分布的空间点作为非固定的随机点。6个基站的理论坐标分别为(0,0,0),(1 965,0,0),(1 452,4 132,0),(-1 100,4 100,500),(-1 100,500,-200),(-1 200,2 000,100),单位为mm。计算每个基站与每个空间点之间的距离,得到各空间点相对于初始点P1的长度变化量Δlnk,因激光跟踪干涉仪的测长不确定度U为0.2 μm+0.3 μm/m,在每个空间点对应的Δlnk中加入[-U,U]的噪声模拟实际情况中的干涉测长变化量。

对比相同标准距离时4种标定方式的标定效果,约束算法的权重均相同,w=1。仿真1为不重组的单组标定,即获取固定点和非固定随机点的干涉测长值各一组,进行常规的标准距离标定。在前者的基础上使每个固定端点的测长获取次数为h=3,仿真2为不重组的三组均值标定,即对每个固定点的3组测长数据取均值后以单组进行常规标准距离的标定。仿真3为重组后不筛选多组取均值标定。仿真4为重组优化标定,根据1.3节所介绍的标定优化方法进行标定。

4种标定得到系统参数和标准距离后,根据参考值求解各自的误差,如图3。

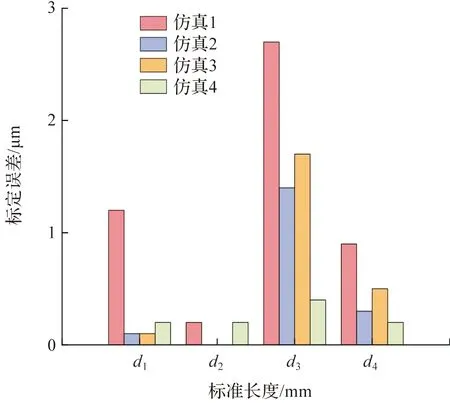
图3 标准长度标定误差Figure 3 Standard length error

图3中从左至右依次表示了标准距离d1、d2、d3、d4的标定误差在4种不同标定方式下的变化,解算结果如表1,仿真1不重组单组标定的标准距离误差最大;仿真2和仿真3两种取均值的标定方式标定的标准长度误差均比仿真1有所减小;仿真4重组优化标定相对前三种标定减小了标准距离的标定误差。

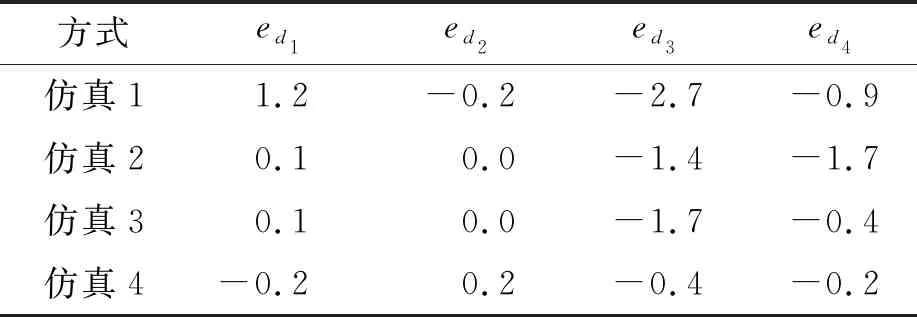
表1 不同标定方式的标准距离误差

计算4种标定方式标定的基站坐标与理论坐标之间的距离,基站坐标标定误差如表2,仿真4的重组优化标定相较仿真1不重组的单组标定,基站坐标最大标定误差由37.3 μm降低到17.4 μm,可见随着标定误差绝对值之和减小,基站坐标标定误差也随之减小。

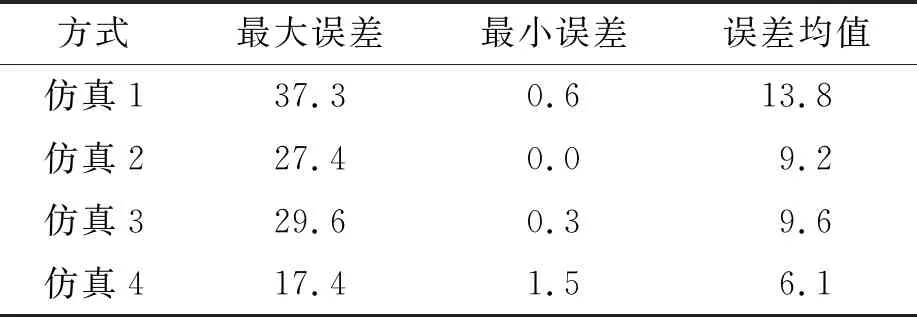
表2 不同标定方式的基站坐标误差

3 实验验证

为了进一步验证标定优化方法的有效性,以及对于不同测量布局的适用性,标定不同测量布局下的系统参数并进行角度测量实验。

3.1 标定实验及结果

实验采用6台激光跟踪干涉仪S1～S6,系统参数设置如1.1节所述,采用两种基站布局进行实验,如图4。6台基站同时跟踪一个靶球,初始点P1作为第一个标定点,靶球在标准距离端点的靶座上被重复放置得到3组标定测长,每次获取六台基站在该点的标定测长,根据标定布局在大理石台上分3个高度的平面均匀选取30个非固定的随机点,共取空间点36个。4段标准距离通过激光跟踪仪提前测量。

图4 基站布局Figure 4 Layout of base station

采用4种方式对两个布局的系统参数进行标定,通过解算的标准距离固定点坐标,计算标准距离标定误差。实验1为不重组的单组标定,实验2为不重组的3组均值标定,实验3为重组不筛选多组取均值标定,实验4为重组优化标定,4种标定方式权重默认为1,结果见表3和表4。

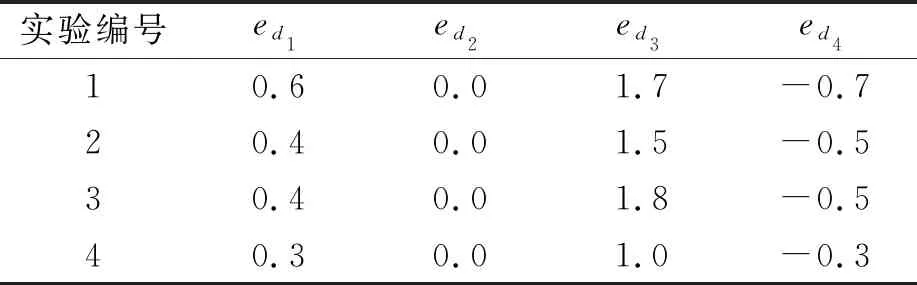
表3 布局1标定结果

表4 布局2标定结果

分别采用4种标定方式标定布局1和布局2的系统参数,不同布局下采用实验4重组优化标定相对实验1不重组的单组标定的标准距离误差均有所降低,实验2和实验3两种取均值的标定方式减少标定误差的效果不及实验4。可见,重组优化标定有效剔除了受测距误差影响较大的标准距离固定点标定测长数据。

3.2 角度测量实验

多边系统测量空间点坐标的测量不确定度与标定不确定度有关,系统测量被测物坐标的误差受标定误差影响。为了对比重组标定优化方法和其他标定方法对测角误差的影响,采用6台激光跟踪干涉仪、1个靶球和分辨率为1″的高精度回转台进行测量。不同布局下均使回转台从零位转动到30°、90°、180°、270°、360°,将转台示值作为参考值。实验装置见图5,靶球放置于初始点P1靶座上采集6台基站的初始测长,再移至转台平面的靶座上开始测量。

图5 角度测量Figure 5 angle measurement

控制转台转动360°,获取6台激光跟踪干涉仪测量的靶球整周的轨迹点,通过最小二乘法对整圆轨迹点拟合得到轨迹的圆心。再使转台转动不同角度,测量靶球在起始点和终点的空间坐标,并结合圆心坐标计算两向量间的夹角,作为测量的角度,将其与转台示值角度作比较。在两种布局下进行实验,采用标定方法1～4各自标定的基站坐标对同组角度测量数据进行解算,各自的测量误差见表5和表6。

表5 布局1实验结果

表6 布局2实验结果

对于布局1的角度测量,分别采用4种标定方式标定的系统参数参与靶球坐标的解算并计算角度。根据表5数据,重组优化标定后测量的角度误差比不重组单组标定和两种取均值的标定得到的误差小。标定1不重组的单组标准距离标定后所测量的角度误差区间为[-7″,8″],重组优化标定后所测量的角度误差区间为[-7″,6″]。

对于布局2的角度测量,分别采用4种标定方式标定的系统参数参与靶球坐标的解算并计算角度。根据表6数据,重组优化标定对应的测量误差依然比其他三种标定对应的误差小。标定1不重组的单组标定后所测量的角度误差区间为[-13″,13″],采用重组优化标定后所测量的角度误差区间为[-11″,11″]。

实验结果表明,在不同布局下,重组优化标定的标准距离误差与不重组单组标定相比有不同程度的减小。同时对比了在增加固定点标定次数时,标定方式2～4的不同数据处理方式对测量结果的影响,表明重组优化标定对于减小测量误差的效果最为明显。布局1中,重组优化标定使测角误差由8″减小到5″;布局2中,重组优化标定使测角误差由13″减小到11″。

4 结 语

本文提出一种多边测量系统的标定优化方法,该优化方法通过增加距离约束固定端点的采集次数,对固定点标定数据重新组合,扩大标定数据组数。组合后的每组标定测长作为标准距离约束算法的约束条件进行迭代求解,剔除标定误差最大的组合,对剩余组继续迭代筛选标定得到标定测长的最优组合。仿真对比了不同标定方式对系统参数标定误差的影响,再通过不同布局的角度测量实验对比了不同标定方法在不同布局下的测量效果。重组优化标定对于两布局角度测量误差区间由[-7″,8″]、[-13″,13″]分别减小为[-7″,6″]、[-11″,11″]。该方法使标准距离的标定误差减小以提高系统参数的标定误差,进而降低了不同布局的测量误差,表明该方法能够有效剔除受干涉测距误差影响较大的固定测长数据,且适用于不同布局。